机器学习——单变量线性回归

房价预测问题

你有一个10000平方英尺的房子，现在要进行转买，能卖多少钱呢？
单变量线性回归，顾名思义是一个变量对结果产生的影响，例如上题房屋面积对房屋价格的影响
回归是统计学的一个重要概念，其本意是根据之前的数据预测一个准确的输出值，解题思路如下：

1、定义一个模型 hθ(x)=θ₀+θ₁x，并初始化θ₀ θ₁的值就会产生一个如下的图像

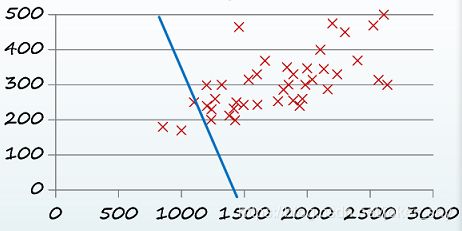
然后就会发现这条直线并不能很好的弥合这些数据，所以需要更新参数，但是更新参数前需要求一下这条直线的代价
2.求代价函数
3.进行梯度下降更新参数并取得θ的最小值

梯度下降后会发现这条线比之前的要好一点，接着我们重复这个步骤，最后我们会获得这样的一个图像

接下来我们就以一个例子来看一下这个流程

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取数据
data = np.loadtxt(r'C:\Users\shy\PycharmProjects\untitled\week3\ex1data1.txt',delimiter=',')
# print(data.shape)
# 数据提取
X = data[:,:-1]
y = data[:,-1]
# 数据初始化
X = np.c_[np.ones(len(X)),X]
y = np.c_[y]


# 定义模型
def model(X,theta):
    h = np.dot(X,theta)
    return h


# 定义代价函数
def costFunc(h,y):
    m = y.shape[0]
    J = 1.0/(2*m)*np.sum(np.square(h-y))
    # J = 1.0/(2*m)*np.dot((h-y).T,(h-y))
    return J


# 定义梯度下降函数
def gradDesc(X,y,alpha=0.01,iter_num=15000):
    m,n = X.shape
    theta = np.zeros((n,1))  # 初始化theta值
    J_history = np.zeros(iter_num)  # 初始化代价函数值

    # 执行梯度下降
    for i in range(iter_num):
        h = model(X,theta)
        J_history[i] = costFunc(h,y)

        deltatheta = (1.0/m)*np.dot(X.T,h-y)
        theta -= alpha*deltatheta
    return J_history,theta


# 调用梯度下降算法
J_history,theta = gradDesc(X,y)


# 画图
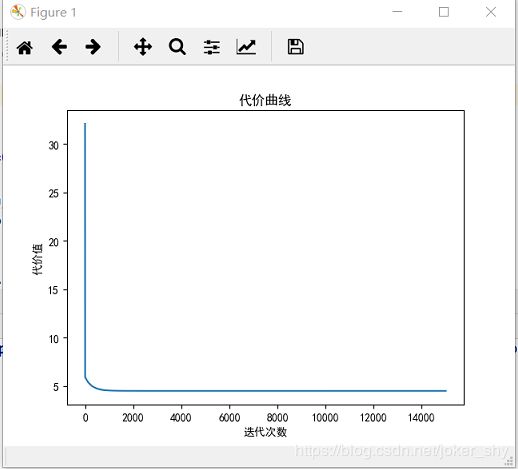
# 画代价曲线
plt.title('代价曲线')
plt.plot(J_history)
plt.xlabel('迭代次数')
plt.ylabel('代价值')
plt.show()

# 画样本散点图和线性回归方程
plt.title('样本分布图')
# 散点图
plt.scatter(X[:,1],y[:,0],c='pink')
# 画回归方程
min_x,max_x = np.min(X[:,1]),np.max(X[:,1])
min_x_y,max_x_y = theta[0]+theta[1]*min_x,theta[0]+theta[1]*max_x
plt.plot([min_x,max_x],[min_x_y,max_x_y])

plt.show()

效果展示

总结

通过这个训练模型，你就能清晰的看出房屋面积对价格的影响，也可以知道10000平方英尺的房子能卖多少了