数值分析大作业

实验流程概述

房价预测kaggle入门项目

1 数值分析的知识点:

1. 数据处理
2. 特征工程
3. 交叉验证4. 岭回归
4. 随机森林
5. 调参

2 题解思路及结果分析

1. 数据读入 pd.read_csv
2. 数据监测 train_df.head()
3. 数据合并 DataFrame
4. 数据平滑化 用log1p
5. 特征工程 标准化变量属性
    类别由int改为string
    类别设置为one-hot编码
    用平均值补全缺失数据
6. 建立岭回归模型 分训练集与测试集
    转DF类型为Numpy Array类型
    掉包构建Ridge Regression模型clf = Ridge(alpha)
    用交叉验证测试模型cross validation
    调试参数观测效果
    遍历alpha调参

(alpha=10~20的时候，可以把score达到0.135左右)

7. 建立随机森林模型(kaggle比赛中用的比较多的一种模型,效果也很好)
    方法与岭回归差不多,也是掉包,但是需要理解随机森林的原理,方便调参数
    调用random forest模型clf = RandomForestRegressor(n_estimators=200, max_features=max_feat)
    遍历max_feat调参

(用RF的最优值达到了0.137)

8. 用Stacking的思维来汲取两种或者多种模型的优点
    取得到的预测
    用expm1()函数把predit的值给exp回去(之前的平滑化操作的逆向还原)
    直接平均化考虑两种模型的综合值
9. 提交结果为DF格式,一列为id,一列为SalePrice

3 思考及反思

思考::

1. 第一次处理这么庞大且高维度的数据,感到有一点吃力,光是数据清洗整理就要很大的工_作量了,从数据清洗中学到很多
2. 对于其中的岭回归和随机森林感到很强大,不过还是会其中的算法原理,光掉包,难以针对不同的有特征的数据采取最合适的参数,并且很影响主观上的参数的选择
3. 交叉验证的使用可以提高有限数据的利用率
   反思::
4. 掉包很方便,千万不要形成依赖,尤其是对数学系而言,就如学习数值分析就是究其算法,我们的核心竞争力就在这了
5. 学会对数据的清理,尤其是大规模数据缺失值的调整

算法分析

1. 脊回归（Ridge Regression）

监督学习

参考
当使用最小二乘法计算线性回归模型参数的时候，如果数据集合矩阵（也叫做设计矩阵(design matrix)）$X$，存在多重共线性，那么最小二乘法对输入变量中的噪声非常的敏感，其解会极为不稳定。为了解决这个问题，就有了这一节脊回归（Ridge Regression ）。

当设计矩阵$X$存在多重共线性的时候（数学上称为病态矩阵），最小二乘法求得的参数$w$在数值上会非常的大，而一般的线性回归其模型是 $y=w^{T}x$ ，显然，就是因为$w$在数值上非常的大，所以，如果输入变量$x$有一个微小的变动，其反应在输出结果上也会变得非常大，这就是对输入变量总的噪声非常敏感的原因。

如果能限制参数$w$的增长，使$w$不会变得特别大，那么模型对输入$w$中噪声的敏感度就会降低。这就是脊回归和套索回归（Ridge Regression and Lasso Regrission）的基本思想。

为了限制模型参数$w$的数值大小，就在模型原来的目标函数上加上一个惩罚项，这个过程叫做正则化（Regularization）。

如果惩罚项是参数的$l2$的范数，就是脊回归(Ridge Regression)

如果惩罚项是参数的$l1$范数，就是套索回归（Lasso Regrission）

正则化同时也是防止过拟合有效的手段，这在“多项式回归”中有详细的说明。

2 随机森林

推荐参考

官方文档解释Random Forests
参考博文帮助解释
随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法

sklearn中随机森林用法

分类
回归
调优

随机森林，简单理解，
比如预测salary，就是构建多个决策树job，age，house，然后根据要预测的量的各个特征（teacher，39，suburb）分别在对应决策树的目标值概率（salary<5000,salary>=5000），从而，确定预测量的发生概率（如，预测出P(salary<5000)=0.3）.

一些参数说明

最主要的两个参数是n_estimators和max_features。
n_estimators：表示森林里树的个数。理论上是越大越好。但是伴随着就是计算时间的增长。但是并不是取得越大就会越好，预测效果最好的将会出现在合理的树个数。
max_features：随机选择特征集合的子集合，并用来分割节点。子集合的个数越少，方差就会减少的越快，但同时偏差就会增加的越快。根据较好的实践经验。如果是回归问题则：
max_features＝n_features，如果是分类问题则max_features＝sqrt(n_features)。

如果想获取较好的结果，必须将max_depth＝None,同时min_sample_split=1。
同时还要记得进行cross_validated（交叉验证），除此之外记得在random forest中，bootstrap=True。但在extra-trees中，bootstrap=False。

3 交叉验证方法

参考
它的基本思想就是将原始数据（dataset）进行分组，一部分做为训练集来训练模型，另一部分做为测试集来评价模型。

实验步骤

实验环境: win10-anaconda-jupyter

1 检测源数据集

import numpy as np
import pandas as pd

1.1 读入数据

一般来说源数据的index那一栏没什么用，但若可以用来作为我们pandas dataframe的index。这样之后要是检索起来也省事儿。

train_df = pd.read_csv('H:/coding/house_price_input/train.csv', index_col=0)
test_df = pd.read_csv('H:/coding/house_price_input/test.csv', index_col=0)

1.2 检查源数据

train_df.head()

	MSSubClass	MSZoning	LotFrontage	LotArea	Street	Alley	LotShape	LandContour	Utilities	LotConfig	...	PoolArea	PoolQC	Fence	MiscFeature	MiscVal	MoSold	YrSold	SaleType	SaleCondition	SalePrice
Id
1	60	RL	65.0	8450	Pave	NaN	Reg	Lvl	AllPub	Inside	...	0	NaN	NaN	NaN	0	2	2008	WD	Normal	208500
2	20	RL	80.0	9600	Pave	NaN	Reg	Lvl	AllPub	FR2	...	0	NaN	NaN	NaN	0	5	2007	WD	Normal	181500
3	60	RL	68.0	11250	Pave	NaN	IR1	Lvl	AllPub	Inside	...	0	NaN	NaN	NaN	0	9	2008	WD	Normal	223500
4	70	RL	60.0	9550	Pave	NaN	IR1	Lvl	AllPub	Corner	...	0	NaN	NaN	NaN	0	2	2006	WD	Abnorml	140000
5	60	RL	84.0	14260	Pave	NaN	IR1	Lvl	AllPub	FR2	...	0	NaN	NaN	NaN	0	12	2008	WD	Normal	250000

5 rows × 80 columns

通过这样的检查,考虑怎样对数据进行更好的整合

2 合并数据

为了用DataFrame进行数据预处理的时候更加方便。等所有的需要的预处理进行完之后，再把他们分隔开。

比如其中SalePrice作为我们的训练目标，只会出现在训练集中，不会在测试集中所以，我们先把SalePrice这一列给拿出来

我们先看一下SalePrice

%matplotlib inline
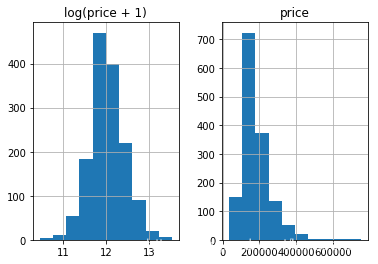
prices = pd.DataFrame({"price":train_df["SalePrice"], "log(price + 1)":np.log1p(train_df["SalePrice"])})
prices.hist()

array([[,
        ]], dtype=object)

可见，label本身并不平滑。为了使分类器的学习更加准确，我们会首先把label给“平滑化”（正态化）

不进行这一步会导致结果总是达不到一定标准。

使用log1p, 也就是 log(x+1)，可以避免了复值的问题。

最后算结果的时候，要记得把预测到的平滑数据给变回去。

log1p()就需要expm1(); 同理，log()就需要exp()

#合并剩下的部分,y_train就是SalePrice那一列
y_train = np.log1p(train_df.pop('SalePrice'))

# 得到何在一块的DataFrame
all_df = pd.concat((train_df, test_df), axis=0)

all_df.shape

(2919, 79)

y_train.head()

Id
1    12.247699
2    12.109016
3    12.317171
4    11.849405
5    12.429220
Name: SalePrice, dtype: float64

3 变量变换

相当于特征工程,即统一不方便处理的数据

标准化变量属性

比如MSSubClass 的值其实应该是一个类别,

Pandas中使用DF的时候，这类数字符号会被默认记成数字。

所以需要把它变回成string

all_df['MSSubClass'].dtypes

dtype('int64')

all_df['MSSubClass'] = all_df['MSSubClass'].astype(str)

统计一下MSSubClass值

all_df['MSSubClass'].value_counts()

20     1079
60      575
50      287
120     182
30      139
160     128
70      128
80      118
90      109
190      61
85       48
75       23
45       18
180      17
40        6
150       1
Name: MSSubClass, dtype: int64

把category的变量转变成numerical表达形式

用One-Hot的方法来表达category。

pandas自带的get_dummies方法，可以一键做到One-Hot。

pd.get_dummies(all_df['MSSubClass'], prefix='MSSubClass').head()

	MSSubClass_120	MSSubClass_150	MSSubClass_160	MSSubClass_180	MSSubClass_190	MSSubClass_20	MSSubClass_30	MSSubClass_40	MSSubClass_45	MSSubClass_50	MSSubClass_60	MSSubClass_70	MSSubClass_75	MSSubClass_80	MSSubClass_85	MSSubClass_90
Id
1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0
2	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0

其中一共有12列,即12个类,是这个类就是1,否则为0

all_dummy_df = pd.get_dummies(all_df)
all_dummy_df.head()

	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	BsmtFinSF2	BsmtUnfSF	...	SaleType_ConLw	SaleType_New	SaleType_Oth	SaleType_WD	SaleCondition_Abnorml	SaleCondition_AdjLand	SaleCondition_Alloca	SaleCondition_Family	SaleCondition_Normal	SaleCondition_Partial
Id
1	65.0	8450	7	5	2003	2003	196.0	706.0	0.0	150.0	...	0	0	0	1	0	0	0	0	1	0
2	80.0	9600	6	8	1976	1976	0.0	978.0	0.0	284.0	...	0	0	0	1	0	0	0	0	1	0
3	68.0	11250	7	5	2001	2002	162.0	486.0	0.0	434.0	...	0	0	0	1	0	0	0	0	1	0
4	60.0	9550	7	5	1915	1970	0.0	216.0	0.0	540.0	...	0	0	0	1	1	0	0	0	0	0
5	84.0	14260	8	5	2000	2000	350.0	655.0	0.0	490.0	...	0	0	0	1	0	0	0	0	1	0

5 rows × 303 columns

处理好numerical变量

因为就算是numerical的变量，也还会有一些小问题。

比如，有一些数据是缺失的：

all_dummy_df.isnull().sum().sort_values(ascending=False).head(10)

LotFrontage     486
GarageYrBlt     159
MasVnrArea       23
BsmtHalfBath      2
BsmtFullBath      2
BsmtFinSF2        1
GarageCars        1
TotalBsmtSF       1
BsmtUnfSF         1
GarageArea        1
dtype: int64

其中LotFrontage中有很多都缺失了行

一般来说，数据集的描述里会写的很清楚，这些缺失都代表着什么。

当然，如果实在没有的话，就靠自己想办法

比如在这里，用平均值来填满这些空缺。

mean_cols = all_dummy_df.mean()
mean_cols.head(10)

LotFrontage        69.305795
LotArea         10168.114080
OverallQual         6.089072
OverallCond         5.564577
YearBuilt        1971.312778
YearRemodAdd     1984.264474
MasVnrArea        102.201312
BsmtFinSF1        441.423235
BsmtFinSF2         49.582248
BsmtUnfSF         560.772104
dtype: float64

all_dummy_df = all_dummy_df.fillna(mean_cols)

再检查一下

all_dummy_df.isnull().sum().sum()

0

标准化numerical数据,不包括One-Hot

检查一下numerical数据有哪些

numeric_cols = all_df.columns[all_df.dtypes != 'object']
numeric_cols

Index(['LotFrontage', 'LotArea', 'OverallQual', 'OverallCond', 'YearBuilt',
       'YearRemodAdd', 'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF',
       'TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF', 'GrLivArea',
       'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'BedroomAbvGr',
       'KitchenAbvGr', 'TotRmsAbvGrd', 'Fireplaces', 'GarageYrBlt',
       'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF',
       'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal',
       'MoSold', 'YrSold'],
      dtype='object')

计算标准分布：(X-X’)/s，使数据平滑

numeric_col_means = all_dummy_df.loc[:, numeric_cols].mean()
numeric_col_std = all_dummy_df.loc[:, numeric_cols].std()
all_dummy_df.loc[:, numeric_cols] = (all_dummy_df.loc[:, numeric_cols] - numeric_col_means) / numeric_col_std

前三步都是对数据的处理

4 建立模型

把数据集分回 训练/测试集

dummy_train_df = all_dummy_df.loc[train_df.index]
dummy_test_df = all_dummy_df.loc[test_df.index]

dummy_train_df.shape, dummy_test_df.shape

((1460, 303), (1459, 303))

Ridge Regression
用Ridge Regression模型看看。

（对于多因子的数据集，这种模型可以方便的把所有的var都无脑的放进去）

from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score

把数据由DF转化成Numpy Array,方便skylearn处理

X_train = dummy_train_df.values
X_test = dummy_test_df.values

用Sklearn自带的cross validation方法来测试模型

alphas = np.logspace(-3, 2, 50)
test_scores = []
for alpha in alphas:
    clf = Ridge(alpha)
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=10, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))

『调参数』，对不同CV值，看看哪个效果更好

import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(alphas, test_scores)
plt.title("Alpha vs CV Error");

alpha=10~20的时候，可以把score达到0.135左右

随机森林模型 Random Forest

from sklearn.ensemble import RandomForestRegressor

max_features = [.1, .3, .5, .7, .9, .99]
test_scores = []
for max_feat in max_features:
    clf = RandomForestRegressor(n_estimators=200, max_features=max_feat)
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=5, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))

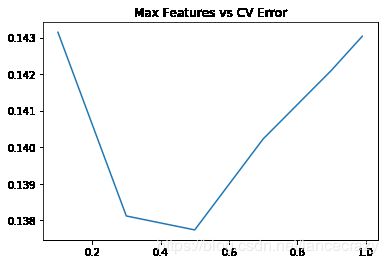
plt.plot(max_features, test_scores)
plt.title("Max Features vs CV Error");

用RF的最优值达到了0.137

5 Ensemble

用一个Stacking的思维来汲取两种或者多种模型的优点

首先，我们把最好的parameter拿出来，做成我们最终的model

ridge = Ridge(alpha=15)
rf = RandomForestRegressor(n_estimators=500, max_features=.3)

ridge.fit(X_train, y_train)
rf.fit(X_train, y_train)

RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
           max_features=0.3, max_leaf_nodes=None,
           min_impurity_decrease=0.0, min_impurity_split=None,
           min_samples_leaf=1, min_samples_split=2,
           min_weight_fraction_leaf=0.0, n_estimators=500, n_jobs=1,
           oob_score=False, random_state=None, verbose=0, warm_start=False)

用expm1()函数把predit的值给exp回去，并且减掉那个"1"

y_ridge = np.expm1(ridge.predict(X_test))
y_rf = np.expm1(rf.predict(X_test))

标准的Ensemble方法：把这群model的预测结果作为新的input，再做一次预测。

简单的方法:就是直接『平均化』。

y_final = (y_ridge + y_rf) / 2

6 提交结果

submission_df = pd.DataFrame(data= {'Id' : test_df.index, 'SalePrice': y_final})

submission_df.head(10)

	Id	SalePrice
0	1461	119477.338695
1	1462	150902.390445
2	1463	174911.212061
3	1464	189160.976998
4	1465	195117.393119
5	1466	175920.151299
6	1467	178552.903310
7	1468	169095.568538
8	1469	184401.158784
9	1470	123935.823190

以上