机器学习算法-09-深度学习、BP神经网络、Hopfield神经网络、基于数学原理的神经网络、径向基函数RBF(B站一条会说666的咸鱼)

Deep Learning 深度学习的概念源于人工神经网络的研究，含多隐层的多层感知器就是有一种深度学些的结构 ，深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征的表示。

概念于2006年由Hinton提出，基于深信度网DBN提出的非监督的贪心逐层训练算法，为解决深层结构相关的优化难题带来希望，随后提出多层自动编码器深层结构。此外Lecun等人提出的卷积神经网络 是第一个真正多层结构学习算法，他利用空间相对关系减少参数数目以提高训练性能。

深度学习的三大大佬
吴恩达 Cousera的创始人 参与Googel Brain 的项目，是百度的首席科学家，全面参与百度研究院的管理，包括百度大脑 计划。

Geoffery Hinton 多伦多大学计算机科学系教授 机器学习人工智能顶级专家，目前领导Googel Brain的项目。

Yann LeCun 人工智能尤其是深度学习领域最知名的学者之一，其在多伦多大学，是从Hinton,1988-2002年加盟贝尔实验室，期间研发了卷积神经网络(Convolutional Neural Networrk)与曾广泛使用的OCR的图像变换网络方法，当然图型压缩技术，DjVu可能更为大家所常见。

前馈神经网络，一般指前馈神经网络或者前馈型神经网络。它是一种最简单的神经网络，各神经元之间分层排列，每个神经元只与前一层的神经元相连，接收前一层的输入，并输出给下一层，数据正向流动，输出仅由当前的输入和网络的权值确定，各层间没有反馈 。包括单层感知器，线性神经网络，BP神经网络 ，RBF神经网络等 。

BP神经网络，所谓的BP神经网络，是在Hebb提出学习规则之后，提出来的误差反向传播法(error BackPropagration) ，是一种多层前馈的神经网络。目前应用最多的最广泛的算法，就是BP神经网络。

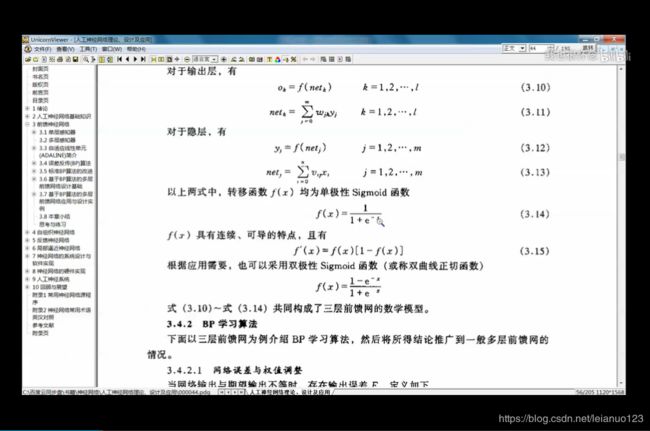
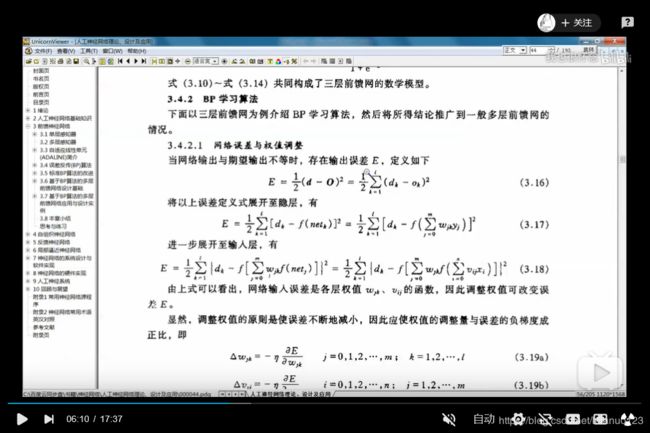
在神经网络中，对外部的环境提供的模式样本进行学习训练，并能储存这种模式，成为感知机，对外部的环境有适应能力，并且能自动的提取外环境的变化特征，则称为认知器。其中我们常见的神经网络，比如说BP神经网络 和hopfiled神经网络。并且这两种神经网络也是常见的有监督的神经网络，需要外接提供相应的学习样本才能进行后续的分析和学习，较常见的单层神经网络，称为三层神经前馈网络，主要包括输入层，隐层能和输出层。通常情况下，隐层的输入，输入的信号在权重系数的作用下，产生一个输出的结果u，再将期待输出的结果和实际输出的结果进行比较，得到误差信号，权值调整结构根据误差值进行调整，从而使误差值变小为0，使得输出信号和实际信号完全一致，则结束学习的过程。

递归神经网络(RNN）是两种神经网络的总称，一种是时间递归神经网络，又名循环神经网络，另一种是结构递归神经网络 。

反馈神经网络(Recurrent Network)又称自联想记忆网络，输出不仅与输入何网络权值有关，还和网络之前输入有关，其目的是设计一个网络，储存一组平衡点，使得当给网络一组初始值时，网络通过自行运行而最终收敛到这个平衡点上，这种神经网络主要包括Hopfiled, Elmman, CG,BSB,CHNN,DHNN,等 。

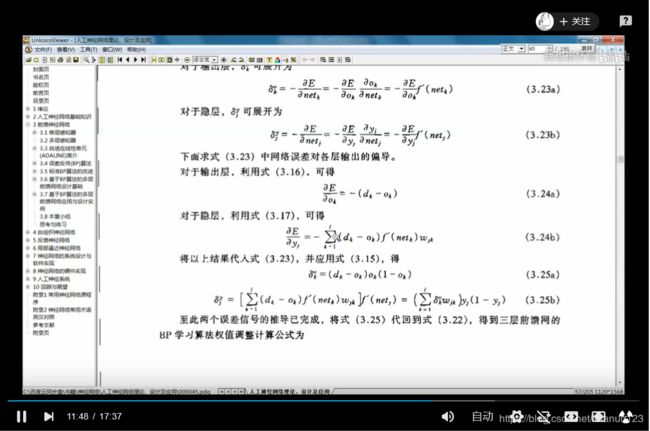
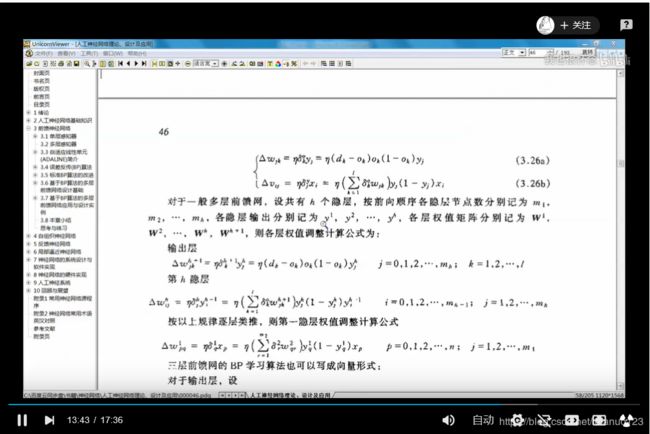
式中的符号代表的是梯度的下降，常数η在(0，1)之间，表示比例系数，在训练中反映了学习的速率，可以看出BP算法属于δ学习规则类，这类算法常被称为误差的梯度下降法(Gradient Descent )算法。

数据的下载

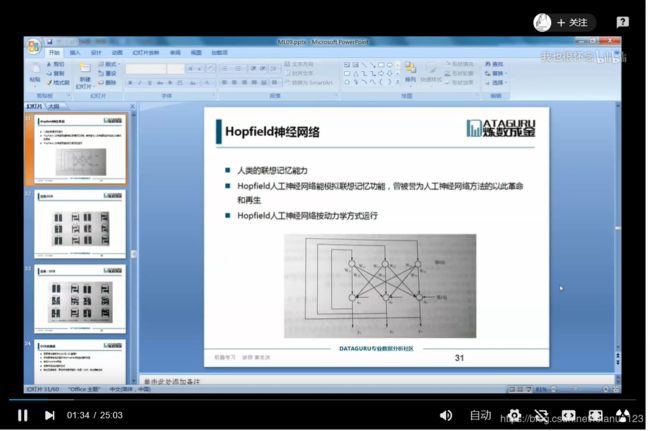
Hopfiled 神经网络
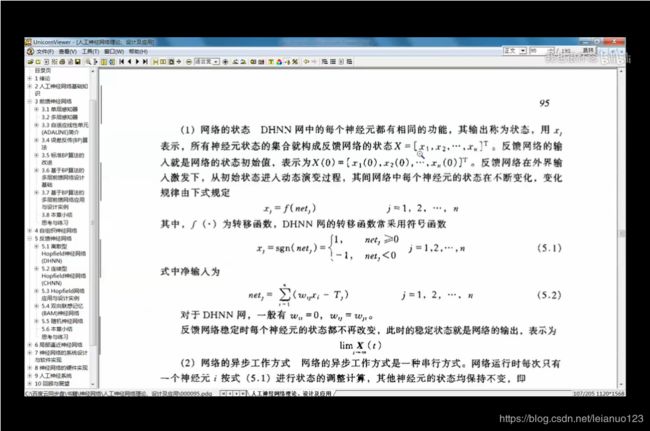
Hopfiled 神经网络是一种单层的反馈，循环的从输入到输出有反馈的联想记忆网络，离散型DHNN(Discrete Hopfiled Neural Network)和连续型CHNN（Countinues Hpfiled Neural Network)。
Hopfiled 最早提出的网络最早提出的时二值神经网络 ，各神经元的激励函数为阶跃函数或者为双极值函数，，神经元的输入和输出只取{0，1},{-1，1}所以也称离散型Hopfiled 神经网络(DHNN）。在DHNN中，所采取的神经元是二值神经元，因此，所输出的离散值0和1或者-1和1分别表示神经元的激活或者抑制状态。离散的Hopfiled神经网络，是一个单层的神经网络，有n神经元节点，每个神经元的输出均接到其他神经元的输入，各节点没有自反馈，每个节点都处于一个可能的状态(1或者-1).既当该神经元所受的刺激超过其他的阈值的时候，神经元就处于一种状态(比如1)，否则神经元就始终处于另一种状态(-1)。

Hopfiled 神经网络的稳定性，Hopfiled神经网络按照动力学的方式运行，对于给定的初始状态按照能量减少的方式演化，最终达到稳定的状态。
DHNN网络实际上是一个离散的非线性的动力学系统。网络从初始状态X(0)开始，若能经有限次递归后，其状态不再发生变化，即t(X+1)=t(X)，则称该网络为稳定的网络。

如果网络是稳定的，则它可以从任何一初态收敛到一个稳定的状态。

如果网络不是稳定的状态，由于DHNN网的每一个节点的状态只有-1和1两种状态，网络不可能出现无限发散的状态，而只能出现限幅的自持振荡，这种网络成为有限环网络。

在有限环网络中，系统在确定的几个状态之间循环往复，系统也可能不稳定收敛到一个稳定的状态，而是在无限多个状态之间变化，但是轨迹并不发散到无穷远。这种现象叫做混沌。

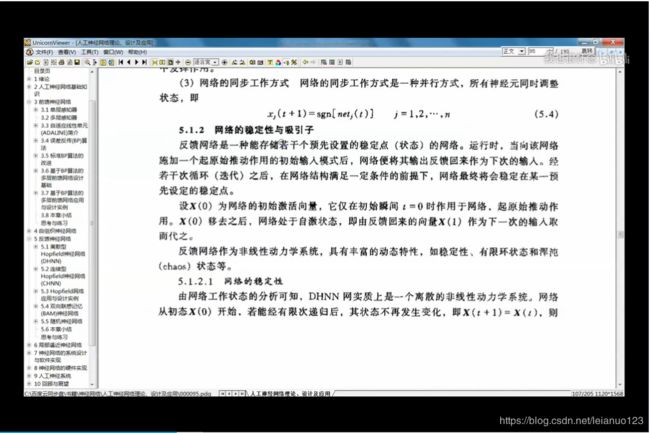
吸引子以及吸引域和能量函数
吸引子网络达到稳定时的状态X，成为网络的吸引子。
吸引域 能够最终演化为该吸引子的初始状态的集合称为该吸引子的吸引域。若按照网络异步方式调整网络，且连接权矩阵W为对称矩阵，则对于任意的初态，网络都最终收敛到一个吸引子。若按照同步的方式调整网络，且连接权矩阵为费负定对称矩阵，则对于任意状态，网络最终都收敛到一个吸引子。

由于网络中的各个节点的状态只能去1或者-1，能量函数E（t）作为网络状态的函数是有下界的。因此网络能量函数能够收敛于一个常数，此时ΔE(t)=0。
因此，当网络工作方式和权矩阵均满足条件时，网络最终将收敛到一个吸引子。

以上分析表明，在网络从初态向稳态装变得过程中，网络的能量始终向减小的方向演变，当能量最终稳定于一个常数时，该常数对应于网络能量的极小状态，称该极小状态为网络的能量井，能量井对应于网络的吸引子。

PCA分析的神经网络

支持向量机神经网络

径向基函数(Radial basis function) 简称RBF，是一个取值依赖于到原点距离的实值函数即t(X)=t(||X||)，此外，也可以按到某一中心点C的距离来定义，任意满足上式的的函数都可以称为径向基函数，其中，范数一般为欧几里得距离，不过亦可以使用其他函数。可以使用很多径向基函数的和来逼近某一给定的函数，这一逼近的过程，可以看成是一个简单的神经网络(RBF中的每一个隐单元看作一个径向基函数，然后再线性加权逼近)。此外机器学习中，径向基函数还被用作支持向量机的核函数。径向基函数可以逼近给定函数的原因。也就是径向基函数如何解决多变量插值问题?从几何意义上看，相当于根据稀疏的给定的样本数据点恢复一个连续的超曲面，在给定点处曲面的值要满足样本值。径向基函数的插值函数如下

可以看出插值函数就是有P个径向基函数和其权值所构成(P为给定的样本数)，那么也就意味着逼近这个超曲面上任何一点可以由对应的基函数值得出
如图(借用其他人的图)

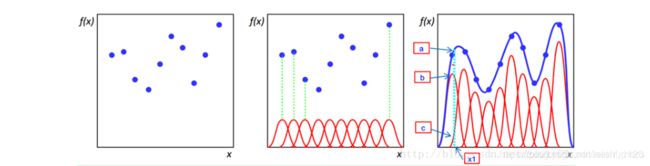
第一幅图即给出二维平面中的n个样本点，然后再构建n个自由基函数，如图二中的红色曲线，假设采用高斯径向基函数其对应的曲线即高斯分布曲线，图三中的蓝色曲线即真正的曲线即真正的曲线，多为情况下即为超曲面。而我们的高斯径向基函数要做的就是要尽可能地用这n个曲线去模拟这条蓝色的曲线。可以看出图三中的蓝色曲线和图二中的蓝色曲线不同，这是由图2曲线乘以一个权值得到的，这也就对应了上面所说的插值函数，就是由n个径向基函数和其权值所构成的。在图3中的X1点，其对应的实际值为f(X1)，而与高斯曲线分别交于b和c两点，径向基高斯函数拟合的结果就是b和c的纵坐标值和，f(X1)-b-c的值就是误差，我们主要通过优化权值参数和选取合适的径向基函数来尽可能地还原蓝色曲线。

RBF网络
BF网络能够逼近任意的非线性函数，可以处理系统内的难以解析的规律性，具有良好的泛化能力，并具有很快的学习收敛速度，业已成功用于 非线性函数逼近，时间序列分析，数据分类和模式识别，图像处理，系统建模控制和故障诊断等。
为什么BF网络具有快速收敛的特点呢?这是因为当网络的一个和多个可调参数(阈值和权值)对任何一个输出都有影响时，这样的网络成为全局逼近网络，由于对于每一次输入，网络上的每一个权值都要调整(如传统的多项式插值法)，从而能导致全局逼近网络的学习速度很慢，比如BF网络。
然鹅，如果对于输入空间的某一个局部之区域只有少数几个连接权值影响输出，则该网络成为局部逼近网络，常见的局部逼近网有RBF网络，小脑模型(CMAC）网络和B样条网络等。

径向基函数网络，通常由三层，主要包括输入层，隐藏层和一个非线性的激活函数和线性径向基径神经网络输出层。输入可以被建模为实属向量，输出时输入向量的一个标量函数。

RBF网络的基本思想是，用RBF作为隐单元的基构成隐含层空间，这样就可以将输入适量直接直接映射到隐空间，而不需要权连接，当RBF的中心点确定后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和，此处的权即为网络可调参数。其中隐函数的作用，就是将向量由低维度的p映射到高纬度的h，这样的话，低维度的线性不可分，到达高纬度就可以变得线性可分了，这里就像支持向量机中的核函数的作用。这也既是核函数的思想。这样网络从输入到输出的映射是非线性，而网络的输出对可调参数而言却又是线性的，网络的权就可以由线性方程组解出，从而大大加快学习的速度。并避免局部极小问题。

那么从RBF函数，如何过渡到RBF网络，如何搭建RBF网络呢?
由上述的内容我们知道，RBF有3层，而对于输入层，我们无法进行优化，只有隐藏层和输出层才可以进行优化，因此RBF就是对两组参数的学习。
1.隐层节点中心，RBF宽度，以及隐层节点数
2.隐层到输出层连接权值

1.方法一，通过非监督的方法得到径向基函数的中心和方差，通过监督的方法(最小均方差)得到隐含层到输出层的权值。具体如下

(1)在训练样本中随机选择h个样本作为h个径向基函数的中心。更好的方法是通过聚类，如K-means聚类得到h各聚类中心，将这些聚类中心当成径向基函数的h个中心。
(2)RBF 神经网络的基函数为高斯函数的时候，方差可由下式求解:

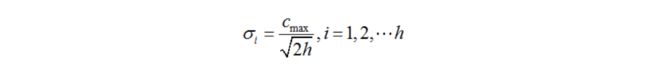
式中的Cmax为所选取中心之间的最大距离，h是隐层节点的个数。扩展函数这么计算是为了比避免径向基函数太尖或太平。

(3)隐含层至输出层之间神经元的连接权值可以用最小均方差LMS直接计算得到，计算公式如下:(计算违逆，d是我们期待的输出值)

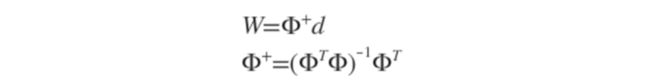
2.方法二
采用监督学习法对网络所有的参数(径向基函数的中心，方差和隐含层到输出层的权值）进行训练。主要是对代价函数(均方差)进行梯度下降，然后修正每个参数，具体如下：
1）随机初始化径向基函数的中心，方差，和隐含层到输出层的权值，当然也可以选择方法1中的方法来初始化径向基函数的中心 。

(2) 通过梯度下降来对网络中的三种参数都进行监督训练优化。代价函数是网络输出和期望输出的均方误差

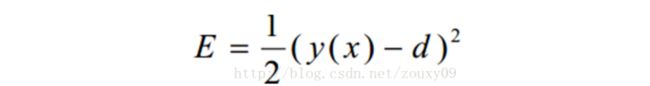
然后每次迭代，在误差梯度的负方向已一定的学习率调整参数。