机器学习之OneHotEncoder独热编码和 LabelEncoder标签编码及实战
学习sklearn和kagggle时遇到的问题,什么是独热编码?为什么要用独热编码?什么情况下可以用独热编码?以及和其他几种编码方式的区别。
首先了解机器学习中的特征类别:连续型特征和离散型特征
拿到获取的原始特征,必须对每一特征分别进行归一化,比如,特征A的取值范围是[-1000,1000],特征B的取值范围是[-1,1].如果使用logistic回归,w1*x1+w2*x2,因为x1的取值太大了,所以x2基本起不了作用。所以,必须进行特征的归一化,每个特征都单独进行归一化。
对于连续性特征:
- Rescale bounded continuous features: All continuous input that are bounded, rescale them to [-1, 1] through x = (2x - max - min)/(max - min). 线性放缩到[-1,1]
- Standardize all continuous features: All continuous input should be standardized and by this I mean, for every continuous feature, compute its mean (u) and standard deviation (s) and do x = (x - u)/s. 放缩到均值为0,方差为1
对于离散性特征:
- Binarize categorical/discrete features: 对于离散的特征基本就是按照one-hot(独热)编码,该离散特征有多少取值,就用多少维来表示该特征。
一. 什么是独热编码?
独热码,在英文文献中称做 one-hot code, 直观来说就是有多少个状态就有多少比特,而且只有一个比特为1,其他全为0的一种码制。举例如下:
假如有三种颜色特征:红、黄、蓝。 在利用机器学习的算法时一般需要进行向量化或者数字化。那么你可能想令 红=1,黄=2,蓝=3. 那么这样其实实现了标签编码,即给不同类别以标签。然而这意味着机器可能会学习到“红<黄<蓝”,但这并不是我们的让机器学习的本意,只是想让机器区分它们,并无大小比较之意。所以这时标签编码是不够的,需要进一步转换。因为有三种颜色状态,所以就有3个比特。即红色:1 0 0 ,黄色: 0 1 0,蓝色:0 0 1 。如此一来每两个向量之间的距离都是根号2,在向量空间距离都相等,所以这样不会出现偏序性,基本不会影响基于向量空间度量算法的效果。
自然状态码为:000,001,010,011,100,101
独热编码为:000001,000010,000100,001000,010000,100000
来一个sklearn的例子:
from sklearn import preprocessing
enc = preprocessing.OneHotEncoder()
enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) # fit来学习编码
enc.transform([[0, 1, 3]]).toarray() # 进行编码输出:array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])
数据矩阵是4*3,即4个数据,3个特征维度。
0 0 3 观察左边的数据矩阵,第一列为第一个特征维度,有两种取值0\1. 所以对应编码方式为10 、01
1 1 0 同理,第二列为第二个特征维度,有三种取值0\1\2,所以对应编码方式为100、010、001
0 2 1 同理,第三列为第三个特征维度,有四中取值0\1\2\3,所以对应编码方式为1000、0100、0010、0001
1 0 2
再来看要进行编码的参数[0 , 1, 3], 0作为第一个特征编码为10, 1作为第二个特征编码为010, 3作为第三个特征编码为0001. 故此编码结果为 1 0 0 1 0 0 0 0 1
二. 为什么要独热编码?
正如上文所言,独热编码(哑变量 dummy variable)是因为大部分算法是基于向量空间中的度量来进行计算的,为了使非偏序关系的变量取值不具有偏序性,并且到圆点是等距的。使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用one-hot编码,会让特征之间的距离计算更加合理。离散特征进行one-hot编码后,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。
为什么特征向量要映射到欧式空间?
将离散特征通过one-hot编码映射到欧式空间,是因为,在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,基于的就是欧式空间。
三 .独热编码优缺点
- 优点:独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间。
- 缺点:当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。
四. 什么情况下(不)用独热编码?
- 用:独热编码用来解决类别型数据的离散值问题,
- 不用:将离散型特征进行one-hot编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用one-hot编码就可以很合理的计算出距离,那么就没必要进行one-hot编码。 有些基于树的算法在处理变量时,并不是基于向量空间度量,数值只是个类别符号,即没有偏序关系,所以不用进行独热编码。 Tree Model不太需要one-hot编码: 对于决策树来说,one-hot的本质是增加树的深度。
总的来说,要是one hot encoding的类别数目不太多,建议优先考虑。
五. 什么情况下(不)需要归一化?
- 需要: 基于参数的模型或基于距离的模型,都是要进行特征的归一化。
- 不需要:基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。
六. 标签编码LabelEncoder
作用: 利用LabelEncoder() 将转换成连续的数值型变量。即是对不连续的数字或者文本进行编号例如:
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit([1,5,67,100])
le.transform([1,1,100,67,5])输出: array([0,0,3,2,1])
>>> le = preprocessing.LabelEncoder()
>>> le.fit(["paris", "paris", "tokyo", "amsterdam"])
LabelEncoder()
>>> list(le.classes_)
['amsterdam', 'paris', 'tokyo'] # 三个类别分别为0 1 2
>>> le.transform(["tokyo", "tokyo", "paris"])
array([2, 2, 1]...)
>>> list(le.inverse_transform([2, 2, 1])) # 逆过程
['tokyo', 'tokyo', 'paris']限制:上文颜色的例子已经提到标签编码了。Label encoding在某些情况下很有用,但是场景限制很多。再举一例:比如有[dog,cat,dog,mouse,cat],我们把其转换为[1,2,1,3,2]。这里就产生了一个奇怪的现象:dog和mouse的平均值是cat。所以目前还没有发现标签编码的广泛使用。
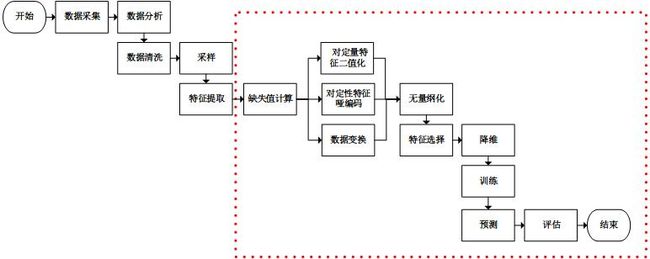
附:基本的机器学习过程
Label encoding在某些情况下很有用,但是场景限制很多。比如有一列 [dog,cat,dog,mouse,cat],我们把其转换为[1,2,1,3,2]。这里就产生了一个奇怪的现象:dog和mouse的平均值是cat。而且像decision tree,random forest和xgboost这种算法能处理好这种转换,而且相比转换前,所需要的内存空间小一点。
One-Hot 编码即独热编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。这样做的好处主要有:1. 解决了分类器不好处理属性数据的问题; 2. 在一定程度上也起到了扩充特征的作用。
将离散型特征进行one-hot编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用one-hot编码就可以很合理的计算出距离,那么就没必要进行one-hot编码。离散特征进行one-hot编码,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。
基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。基于参数的模型或基于距离的模型,都是要进行特征的归一化。Tree Model不太需要one-hot编码: 对于决策树来说,one-hot的本质是增加树的深度。
one hot encoding的优点就是它的值只有0和1,不同的类型存储在垂直的空间。缺点就是,当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。
总的来说,要是one hot encoding的类别数目不太多,建议优先考虑。
七、Sklearn的LabelEncoder和OneHotEncoder实战
LabelEncoder和OneHotEncoder
我们也可以通过sklearn的模块实现对离散变量的one-hot编码,其中LabelEncoder是将离散变量替换为数字,
OneHotEncoder则实现对替换为数字的离散变量进行one-hot编码。
注:get_dummies()可以直接对字符型变量进行one-hot编码,但OneHotEncoder不能直接对字符型变量编码,因此我们需要先将字符型变量转换为数值型变量。这就是为什么在OneHotEncoder之前需要LabelEncoder的原因。
如下代码为将一列数据进行one-hot编码后,然后拼接
all_weekday_cache={}
for e in allday:
all_weekday_cache[e]=pd.to_datetime(e).isoweekday()
traindata['weekday']=traindata['sampleday'].apply(lambda x:all_weekday_cache[x])
if flag=="train":
Enc_ohe.fit(traindata[['weekday']])
print(Enc_ohe.categories_)
print(list(Enc_ohe.categories_[0]))
DF_dummies2 = pd.DataFrame(Enc_ohe.transform(traindata[['weekday']]).todense(), columns = list(Enc_ohe.categories_[0]))
print(DF_dummies2.head(3))
#拼接
traindata = pd.concat((traindata,DF_dummies2),axis=1) # 1 水平方向拼接打印如下:
[array([1., 2., 3., 4., 5., 6., 7.])]
[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0]
1.0 2.0 3.0 4.0 5.0 6.0 7.0
0 0.0 1.0 0.0 0.0 0.0 0.0 0.0
1 0.0 0.0 1.0 0.0 0.0 0.0 0.0
2 0.0 0.0 0.0 0.0 1.0 0.0 0.0
例1
1
from sklearn.preprocessing import OneHotEncoder
2
ohe = OneHotEncoder()
3
ohe.fit([[1,1],[2,1],[3,2],[4,5]])
4
ohe.transform([[2,1],[3,1],[1,1],[4,5]]).toarray()
/home/bigdevelp_user/anaconda3/lib/python3.6/site-packages/sklearn/preprocessing/_encoders.py:368: FutureWarning: The handling of integer data will change in version 0.22. Currently, the categories are determined based on the range [0, max(values)], while in the future they will be determined based on the unique values.
If you want the future behaviour and silence this warning, you can specify "categories='auto'".
In case you used a LabelEncoder before this OneHotEncoder to convert the categories to integers, then you can now use the OneHotEncoder directly.
warnings.warn(msg, FutureWarning)
array([[0., 1., 0., 0., 1., 0., 0.],
[0., 0., 1., 0., 1., 0., 0.],
[1., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0., 0., 1.]])
ohe.categories_
1
ohe.categories_
[array([1., 2., 3., 4.]), array([1., 2., 5.])]
例2
r
1
from sklearn.preprocessing import OneHotEncoder
2
ohe = OneHotEncoder()
3
ohe.fit([[1],[2],[3],[4]])
4
ohe.transform([[2],[3],[1],[4]]).toarray()
/home/bigdevelp_user/anaconda3/lib/python3.6/site-packages/sklearn/preprocessing/_encoders.py:368: FutureWarning: The handling of integer data will change in version 0.22. Currently, the categories are determined based on the range [0, max(values)], while in the future they will be determined based on the unique values.
If you want the future behaviour and silence this warning, you can specify "categories='auto'".
In case you used a LabelEncoder before this OneHotEncoder to convert the categories to integers, then you can now use the OneHotEncoder directly.
warnings.warn(msg, FutureWarning)
array([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 0., 0., 1.]])
1
ohe.categories_
[array([1., 2., 3., 4.])]
例3
1
from sklearn.preprocessing import LabelEncoder
2
le = LabelEncoder()
3
le.fit([1,5,67,100])
4
le.transform([1,1,100,67,5])
array([0, 0, 3, 2, 1])
[
1
from sklearn.preprocessing import LabelEncoder
2
le = LabelEncoder()
3
le.fit([[1,5,67,100],[2,3,4,5]])
4
le.transform([[1,100,67,5],[2,3,4,5]])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
in ()
1 from sklearn.preprocessing import LabelEncoder
2 le = LabelEncoder()
----> 3 le.fit([[1,5,67,100],[2,3,4,5]])
4 le.transform([[1,100,67,5],[2,3,4,5]])
~/anaconda3/lib/python3.6/site-packages/sklearn/preprocessing/label.py in fit(self, y)
217 self : returns an instance of self.
218 """
--> 219 y = column_or_1d(y, warn=True)
220 self.classes_ = _encode(y)
221 return self
~/anaconda3/lib/python3.6/site-packages/sklearn/utils/validation.py in column_or_1d(y, warn)
795 return np.ravel(y)
796
--> 797 raise ValueError("bad input shape {0}".format(shape))
798
799
ValueError: bad input shape (2, 4)
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
sns.set()
%matplotlib inline
#Iris Plot
iris = load_iris()
n_samples, m_features = iris.data.shape
#Load Data
X, y = iris.data, iris.target
D_target_dummy = dict(zip(np.arange(iris.target_names.shape[0]), iris.target_names))
DF_data = pd.DataFrame(X,columns=iris.feature_names)
DF_data["target"] = pd.Series(y).map(D_target_dummy)
#sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
#0 5.1 3.5 1.4 0.2
#1 4.9 3.0 1.4 0.2
#2 4.7 3.2 1.3 0.2
#3 4.6 3.1 1.5 0.2
#4 5.0 3.6 1.4 0.2
#5 5.4 3.9 1.7 0.4
DF_dummies = pd.get_dummies(DF_data["target"])
#setosa versicolor virginica
#0 1 0 0
#1 1 0 0
#2 1 0 0
#3 1 0 0
#4 1 0 0
#5 1 0 0
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
def f1(DF_data):
Enc_ohe, Enc_label = OneHotEncoder(), LabelEncoder()
DF_data["Dummies"] = Enc_label.fit_transform(DF_data["target"])
DF_dummies2 = pd.DataFrame(Enc_ohe.fit_transform(DF_data[["Dummies"]]).todense(), columns = Enc_label.classes_)
return(DF_dummies2)
%timeit pd.get_dummies(DF_data["target"])
#1000 loops, best of 3: 777 µs per loop
%timeit f1(DF_data)
#100 loops, best of 3: 2.91 ms per loop
注:get_dummies返回的为数据框,OneHotEncoder返回的为数组。
>>> from sklearn.preprocessing import OneHotEncoder
>>> enc = OneHotEncoder()
>>> enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]])
>>> enc.n_values_
array([2, 3, 4])
>>> enc.feature_indices_
array([0, 2, 5, 9])
>>> enc.transform([[0, 1, 1]]).toarray()
array([[ 1., 0., 0., 1., 0., 0., 1., 0., 0.]])
One-Hot 编码即独热编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。这样做的好处主要有:1. 解决了分类器不好处理属性数据的问题; 2. 在一定程度上也起到了扩充特征的作用。
将离散型特征进行one-hot编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用one-hot编码就可以很合理的计算出距离,那么就没必要进行one-hot编码。离散特征进行one-hot编码,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。
基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。基于参数的模型或基于距离的模型,都是要进行特征的归一化。Tree Model不太需要one-hot编码: 对于决策树来说,one-hot的本质是增加树的深度。
one hot encoding的优点就是它的值只有0和1,不同的类型存储在垂直的空间。缺点就是,当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。总的来说,要是one hot encoding的类别数目不太多,建议优先考虑。
- one hot 编码及数据归一化
- 对于非负数类型编码 利用onehotEncode
- 对于字符以及混合类型编码 利用labelEncode
# 简单来说 LabelEncoder 是对不连续的数字或者文本进行编号
# sklearn.preprocessing.LabelEncoder():标准化标签,将标签值统一转换成range(标签值个数-1)范围内
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit([1,5,67,100])
le.transform([1,1,100,67,5])
out: array([0, 0, 3, 2, 1], dtype=int64)
#OneHotEncoder 用于将表示分类的数据扩维:
from sklearn.preprocessing import OneHotEncode
ohe = OneHotEncoder()
ohe.fit([[1],[2],[3],[4]])
ohe.transform([[2],[3],[1],[4]]).toarray()
out:array([[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]])
Examples
--------
Given a dataset with three features and four samples, we let the encoder
find the maximum value per feature and transform the data to a binary
one-hot encoding.
>>> from sklearn.preprocessing import OneHotEncoder
>>> enc = OneHotEncoder()
>>> enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], \
[1, 0, 2]]) # doctest: +ELLIPSIS
OneHotEncoder(categorical_features='all', dtype=<... 'numpy.float64'>,
handle_unknown='error', n_values='auto', sparse=True)
>>> enc.n_values_
array([2, 3, 4])
>>> enc.feature_indices_
array([0, 2, 5, 9])
>>> enc.transform([[0, 1, 1]]).toarray()
array([[ 1., 0., 0., 1., 0., 0., 1., 0., 0.]])
Examples
--------
`LabelEncoder` can be used to normalize labels.
>>> from sklearn import preprocessing
>>> le = preprocessing.LabelEncoder()
>>> le.fit([1, 2, 2, 6])
LabelEncoder()
>>> le.classes_
array([1, 2, 6])
>>> le.transform([1, 1, 2, 6]) #doctest: +ELLIPSIS
array([0, 0, 1, 2]...)
>>> le.inverse_transform([0, 0, 1, 2])
array([1, 1, 2, 6])
It can also be used to transform non-numerical labels (as long as they are
hashable and comparable) to numerical labels.
>>> le = preprocessing.LabelEncoder()
>>> le.fit(["paris", "paris", "tokyo", "amsterdam"])
LabelEncoder()
>>> list(le.classes_)
['amsterdam', 'paris', 'tokyo']
>>> le.transform(["tokyo", "tokyo", "paris"]) #doctest: +ELLIPSIS
array([2, 2, 1]...)
>>> list(le.inverse_transform([2, 2, 1]))
['tokyo', 'tokyo', 'paris']
-
LabelEncoder和OneHotEncoder 在特征工程中的应用
-
下面引入scikit learn中的OneHotEncoder的介绍。
http://scikit-learn.org/stable/modules/preprocessing.html#preprocessing
八、pandas的get_dummies
pd.get_dummies(prefix=)
pandas的get_dummies()可以直接对变量进行one-hot编码,其中prefix是为one-hot编码后的变量进行命名。
get_dummies()也可以对某一列数据进行。
DF_dummies = pd.get_dummies(DF_data["target"])
#setosa versicolor virginica
#0 1 0 0
#1 1 0 0
#2 1 0 0
#3 1 0 0
#4 1 0 0
#5 1 0 0相关参考:
https://www.cnblogs.com/king-lps/p/7846414.html
https://blog.csdn.net/Mr_HHH/article/details/80006971