数据结构基础温故-6.查找(上):基本查找与树表查找
只要你打开电脑,就会涉及到查找技术。如炒股软件中查股票信息、硬盘文件中找照片、在光盘中搜DVD,甚至玩游戏时在内存中查找攻击力、魅力值等数据修改用来作弊等,都要涉及到查找。当然,在互联网上查找信息就更加是家常便饭。查找是计算机应用中最常用的操作之一,也是许多程序中最耗时的一部分,查找方法的优劣对于系统的运行效率影响极大。因此,本篇讨论一些查找方法。
一、顺序查找
1.1 基本思想
顺序查找(Sequential Search)又叫线性查找,是最基本的查找技术,它的查找过程是:从表中第一个(或最后一个)记录开始,逐个进行记录的关键字和给定值比较,若某个记录的关键字和给定值相等,则查找成功,找到所查的记录;如果直到最后一个(或第一个)记录,其关键字和给定值比较都不等时,则表中没有所查的记录,查找不成功。
顺序查找所用时间与查找关键字Key在线性表中的位置有关,其时间复杂度为O(n)。顺序查找的优点在于:算法简单易行,且对表的结构无任何要求(无论是顺序表还是链表,也无论是按关键字有序还是无序存放)。当然,其缺点也比较明显:算法效率较低,在较大规模的数据集合中进行查找时,不宜采用顺序查找。
1.2 代码实现
static void SequenceSearchDemo()
{
int[] seqList = { 2, 8, 10, 13, 21, 36, 51, 57, 62, 69 };
Console.WriteLine("-------------基本顺序查找-------------");
Console.WriteLine("查找51:{0}", SequenceSearch(seqList, 51));
Console.WriteLine("查找8:{0}", SequenceSearch(seqList, 8));
Console.WriteLine("查找15:{0}", SequenceSearch(seqList, 15));
}
static int SequenceSearch(int[] seqList, int key)
{
int index = -1;
for (int i = 0; i < seqList.Length; i++)
{
if (seqList[i] == key)
{
index = i;
break;
}
}
return index;
}运行结果为:
二、二分查找
2.1 基本思想
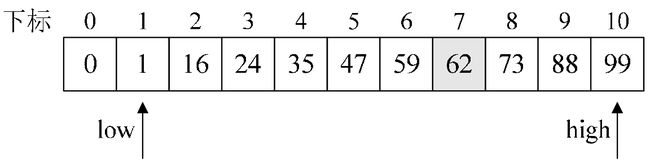
折半查找(Binary Search)技术,又称为二分查找。它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须采用顺序存储,其时间复杂度为O(logn)。
折半查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
2.2 代码实现
static void SeqSearchDemo()
{
int[] seqList = { 2, 8, 10, 13, 21, 36, 51, 57, 62, 69 };
Console.WriteLine("-------------基本二分查找-------------");
Console.WriteLine("查找51:{0}", SeqSearch(seqList, 51));
Console.WriteLine("查找8:{0}", SeqSearch(seqList, 8));
Console.WriteLine("查找15:{0}", SeqSearch(seqList, 15));
}
static int SeqSearch(int[] seqList, int key)
{
int low = 0;
int high = seqList.Length - 1;
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if (seqList[mid] == key)
{
return mid;
}
else if (seqList[mid] < key)
{
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return -1;
}运行结果为:
2.3 Array.BinarySearch方法
在.NET中的数组类Array中,内置了一个二分查找的方法—Array.BinarySearch,它是一个静态方法。需要注意的是:在调用这个方法前,需要确保作为参数的查找表内的关键字已经有序,否则就需要手动调用Array.Sort()方法进行排序。
int[] seqList = { 32, 25, 8, 10, 13, 21, 36, 51, 57, 62, 69 };
Console.WriteLine("-------------Array.BinarySearch-------------");
Array.Sort(seqList);
Console.WriteLine("查找51:{0}", Array.BinarySearch(seqList, 51));
Console.WriteLine("查找69:{0}", Array.BinarySearch(seqList, 69));
Console.WriteLine("查找15:{0}", Array.BinarySearch(seqList, 15));在Array.BinarySearch()方法内部的求mid值的公式为:mid=low+((high-low)>>1),这是因为整数右移一位相当于整数除2操作,但位移运算的速度快于除法运算。
2.4 System.Collections.SortedList类
在.NET中的System.Collections命名空间下,SortedList和SortedList
SortedList studentList = new SortedList();
studentList.Add("005", "张三");
studentList.Add("004", "李四");
studentList.Add("006", "王五");
studentList.Add("012", "马六");
studentList.Add("002", "钱七");
studentList.Add("009", "刘八");
foreach (var item in studentList)
{
Console.WriteLine("{0}:{1}", item.Key, item.Value);
} 运行结果为:
回过头来,我们看看SortedList类的Add方法,从中可以发现,它借助了Array.BinarySearch方法获取存储位置,也就是说它也使用了二分查找方法。
三、查找树方法
前面讨论的几种查找方法中,二分查找效率最高,但其要求表中记录按照关键字有序,且只能在顺序表上实现,从而需要在插入和删除操作时移动很多的元素。如果不希望表中记录按关键字有序,而又希望得到较高的插入和删除效率,可以考虑使用几种特殊的二叉树或树作为表的组织形式。
3.1 二叉查找树
(1)基本概念
二叉查找树(Binary Search Tree,BST)又称二叉排序树,它是满足如下性质的二叉树:
- 若它的左子树非空,则左子树上所有记录的值均小于根记录的值;
- 若它的右子树非空,则右子树上所有记录的值均大于根记录的值;
- 左、右子树又各是一棵二叉查找树。
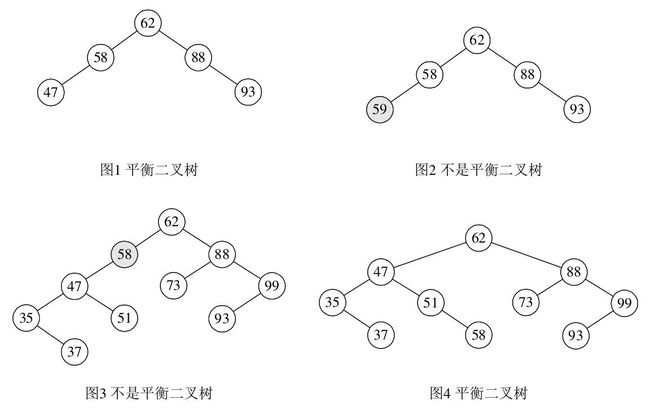
假如有一个序列{62,88,58,47,35,73,51,99,37,93},那么构造出来的二叉查找树如下图所示:
二叉查找树是递归定义的,其一般理解是:二叉查找树中任一节点,其值为k,只要该节点有左孩子,则左孩子的值必小于k,只要有右孩子,则右孩子的值必大于k。二叉查找树的一个重要的性质是:中序遍历该树得到的序列是一个递增有序的序列。
(2)二叉查找树的新增操作
(3)二叉查找树的删除操作
(4)二叉查找树的代码实现
有关二叉查找树的新增和删除节点如何实现,可以阅读《数据结构基础温故—4.树(中)》一文,该文使用C#实现了二叉查找树。
注意:对于二叉查找树最糟糕的情况是插入一个有序序列,使得具有N个元素的集合生成了高度为N的单枝二叉树,从而使其退化了一个单链表,其查找效率也会会由O(logn)变为O(n)。
3.2 平衡二叉树
刚刚提到在二叉查找树中,如果插入元素的顺序接近有序,那么二叉查找树将退化为链表,从而导致二叉查找树的查找效率大大降低。前苏联两位科学家G.M. Adelson-Velskii和E.M. Landis在1962年的一篇论文中提出了一种自平衡二叉查找树。这种二叉查找树在插入和删除操作中,可以通过一系列的旋转操作来保持平衡,从而保证了二叉查找树的查找效率。最终这种二叉查找树被命名为AVL-Tree,也被称为平衡二叉树。
(1)基本概念
平衡二叉树定义(AVL):它或者是一颗空树,或者具有以下性质的二叉树:它的左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
平衡因子(BF):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1;
PS:平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的
(2)平衡二叉树的操作
假设我们已经有棵平衡二叉树,现在让我们来看看插入节点后,原来节点失去平衡后,平衡二叉树会进行不同类型(RR、LL、LR以及RL)的旋转来保持平衡。
3.3 System.Collections.Generic.SortedDictionary类
另一种与平衡二叉树类似的是红黑树,红黑树和AVL树的区别在于它使用颜色来标识节点的高度,它所追求的是局部平衡而不是AVL树中的非常严格的平衡。在.NET中的System.Collections.Generic命名空间下,SortedDictionary类就是使用红黑树实现的。红黑树和AVL树的原理非常接近,但是复杂度却远胜于AVL树,这里也就不做讨论。园子里也已经有了不少关于红黑树的比较好的介绍的文章,有兴趣的可以去阅读阅读。
在代码中,我们可以模拟100000个数字进行添加:
Random random = new Random();
int array_count = 100000;
List intList = new List();
for (int i = 0; i <= array_count; i++)
{
int ran = random.Next();
intList.Add(ran);
}
SortedDictionary dic_int = new SortedDictionary();
foreach (var item in intList)
{
if (dic_int.ContainsKey(item) == false)
{
dic_int.Add(item, item);
}
} 当然,还可以与SortedList(SortedList内部是Array,而SortedDictionary内部是红黑树)进行一下对比,这里使用了老赵的CodeTimer类:
(1)新增操作对比
由于SortedList用Array数组保存,每次进行插入操作时,首先用二分查找法找到相应的位置,得到位置以后,SortedList会把该位置以后的值依次往后移一个位置,空出当前位,再把值插入,这个过程中用到了Array.Copy方法,而调用该方法是比较损耗性能的,该代码如下:
private void Insert(int index, TKey key, TValue value)
{
......
if (index < this._size)
{
Array.Copy(this.keys, index, this.keys, index + 1, this._size - index);
Array.Copy(this.values, index, this.values, index + 1, this._size - index);
}
......
}SortedDictionary在添加操作时,只会根据红黑树的特性,旋转节点,保持平衡,并没有对Array.Copy的调用。下面我们就用数据测试一下:循环一个int型、容量为10w的随机数组,分别用SortedList和SortedDictionary添加,看看效率如何:
static void SortedAddInTest()
{
Random random = new Random();
int array_count = 100000;
List intList = new List();
for (int i = 0; i <= array_count; i++)
{
int ran = random.Next();
intList.Add(ran);
}
SortedList sortedlist_int = new SortedList();
SortedDictionary dic_int = new SortedDictionary();
CodeTimer.Time("sortedList_Add_int", 1, () =>
{
foreach (var item in intList)
{
if (sortedlist_int.ContainsKey(item) == false)
sortedlist_int.Add(item, "test" + item.ToString());
}
});
CodeTimer.Time("sortedDictionary_Add_int", 1, () =>
{
foreach (var item in intList)
{
if (dic_int.ContainsKey(item) == false)
dic_int.Add(item, "test" + item.ToString());
}
});
} 运行结果如下图所示:
从上图可以看出:在大量添加操作的情况下,SortedDictionary性能(无论是从时间消耗、CPU计算、还是GC垃圾回收次数)优于SortedList。
(2)查询操作对比
两者的查询操作中,时间复杂度都为O(logn),且源码中也没有额外的操作造成性能损失,那么他们在查询操作中性能如何?继续上面一个例子进行测试。
static void SortedQueryInTest()
{
Random random = new Random();
int array_count = 100000;
List intList = new List();
for (int i = 0; i <= array_count; i++)
{
int ran = random.Next();
intList.Add(ran);
}
SortedList sortedlist_int = new SortedList();
SortedDictionary dic_int = new SortedDictionary();
foreach (var item in intList)
{
if (sortedlist_int.ContainsKey(item) == false)
sortedlist_int.Add(item, "test" + item.ToString());
}
foreach (var item in intList)
{
if (dic_int.ContainsKey(item) == false)
dic_int.Add(item, "test" + item.ToString());
}
CodeTimer.Time("sortedList_Search_int", 1, () =>
{
foreach (var item in intList)
{
sortedlist_int.ContainsKey(item);
}
});
CodeTimer.Time("sortedDictionary_Search_int", 1, () =>
{
foreach (var item in intList)
{
dic_int.ContainsKey(item);
}
});
} 运行结果如下图所示:
从上图可以看出:两者在循环10w次的情况下,查询操作SortedList大概为SortedDictionary的一半,这是由于SortedList已经在插入操作时已经将其转化为了一个有序的数组,从而在查询时可以直接使用二分查找提高效率。SortedDictionary则是一个二叉排序树,查询效率理论上也是O(logn),但其较有序数组的二分查找效率还是差了一点点。
(3)删除操作对比
从添加操作例子可以看出,由于SortedList内部使用Array数组进行存储数据,而数组本身的局限性使得SortedList大部分的添加操作都要调用Array.Copy方法,从而导致了性能的损失,这种情况同样存在于删除操作中。
SortedList每次删除操作都会将删除位置后的值往前挪动一位,以填补删除位置的空白,这个过程刚好跟添加操作反过来,同样也需要调用Array.Copy方法,相关代码如下:
public void RemoveAt(int index)
{
......
if (index < this._size)
{
Array.Copy(this.keys, index + 1, this.keys, index, this._size - index);
Array.Copy(this.values, index + 1, this.values, index, this._size - index);
}
......
}而SortedDictionary使用红黑树结构存储元素,红黑树本身是一棵二叉查找树,它的删除和二叉查找树的删除类似。首先要找到真正的删除点,当被删除结点n存在左右孩子时,真正的删除点应该是n的中序遍历的前驱,关于这一点请参考二叉查找树的删除。如下图所示,当删除结点20时,实际被删除的结点应该为18,结点20的数据变为18。
这里,我们仍然选择上面的例子来进行一个简单的对比测试,仍然是10w个元素的数据量:
static void SortedDeleteInTest()
{
Random random = new Random();
int array_count = 100000;
List intList = new List();
for (int i = 0; i <= array_count; i++)
{
int ran = random.Next();
intList.Add(ran);
}
SortedList sortedlist_int = new SortedList();
SortedDictionary dic_int = new SortedDictionary();
foreach (var item in intList)
{
if (sortedlist_int.ContainsKey(item) == false)
sortedlist_int.Add(item, "test" + item.ToString());
}
foreach (var item in intList)
{
if (dic_int.ContainsKey(item) == false)
dic_int.Add(item, "test" + item.ToString());
}
CodeTimer.Time("sortedList_Delete_String", 1, () =>
{
foreach (var item in intList)
{
sortedlist_int.Remove(item);
}
});
CodeTimer.Time("sortedDictionary_Delete_String", 1, () =>
{
foreach (var item in intList)
{
dic_int.Remove(item);
}
});
} 运行结果如下图所示:
从上图也可以看出:在10w次的删除操作中,SortedDictionary的处理速度和性能消耗较SortedList好的不是一丁半点。
总结:
①SortedList用数组存储数据,所以对GC比较友好一点,而且对于相对比较有序的输入源而言,操作较少(eg:List
intList = Enumerable.Range(0, array_count).ToList())。
②SortedDictionary用节点链存储数据,所以对GC而言,相对比较复杂。所以当可以预见到集合中的元素比较少的时候或者数据本身相对比较有序时,应该倾向于使用SortedList。
参考资料
(1)程杰,《大话数据结构》
(2)陈广,《数据结构(C#语言描述)》
(3)段恩泽,《数据结构(C#语言版)》
(4)许两会,《.NET集合类的研究—有序集合(SortedDictionary)》
特别感谢
太原理工大学,数据结构算法演示网站
作者:周旭龙
出处:http://edisonchou.cnblogs.com