ICP算法的推导和实现

1 ICP算法的推导

• Reference Paper： LiDAR-Camera Calibration using 3D-3D Point correspondences

目标函数， $Q$为target cloud， $P$为source cloud

$$F(t)=\sum _{i=1}^n{\Vert \left(R{P}_i+t\right)-Q_i\Vert }^2$$
首先对$t$进行求导，
$$\begin{array}{c}\frac{\partial F(t)}{\partial t}=2{\sum }_{i=1}^n\left(R{P}_i+t\right)-Q_i=0\\ \frac{\partial F(t)}{\partial t}=2R{\sum }_{i=1}^n{P}_i+2t{\sum }_{i=1}^{n}1-2{\sum }_{i=1}^n{Q}_i\end{array}$$
发现求出$R$之后再去求解$t$会非常简单，
$$t=\frac{1}{n}\sum _{i=1}^n{Q}_i-R\frac{1}{n}\sum _{i=1}^n{P}_i$$
$$t=\bar{Q}-R\bar{P}$$
将优化问题转化为只和$R$有关
$$R=\underset{R\in SO(3)}{\mathrm{argmin}}\Vert (R\left(P_i-\bar{P}\right)-\left(Q_i-\bar{Q}\right){\Vert }^2$$

$$X_i=\left(P_i-\bar{P}\right),Y_i=\left(Q_i-\bar{Q}\right)$$
对式子进行展开，发现
$$\begin{gathered} R=\underset{R\in SO(3)}{\mathrm{argmin}}\sum \Vert R{X}_i-Y_i{\Vert }^2 \\ =Tr(\sum \Vert R{X}_i-Y_i{\Vert }^2) \\ =\sum Tr(\Vert R{X}_i-Y_i{\Vert }^2) \\ =\sum (Tr(X_i^T{R}^{T}R{X}_i)+Tr(Y_i^T{Y}_i)-2Tr(Y_i^{T}R{X}_i)) \end{gathered}$$
发现前两项和$R$没有关系
优化问题转化为
$$\begin{gathered} R=\underset{R\in SO(3)}{\mathrm{argmax}}\sum Tr(Y_i^{T}R{X}_i)) \\ =\sum Tr(R{X}_i{Y}_i^T)) \\ =Tr(R\sum X_i{Y}_i^T) \\ =Tr(R{X}_{3\times n}{Y}_{3\times n}^T) \end{gathered}$$
做svd分解
$$X{Y}^T=UD{V}^T$$
$$\begin{gathered} R=\underset{R\in SO(3)}{\mathrm{argmax}}Tr(RX{Y}^T) \\ =Tr(RUD{V}^T) \\ =Tr(V^{T}RUD) \end{gathered}$$
let
$$M=V^{T}RU$$
有
$$Tr(MD)=\sum M_{ii}{d}_i<=\sum d_i$$
此时$$M=I=V^{T}RU$$
得到$$R=V{U}^T$$
$R$应该满足正交矩阵的条件，并且$det(R)=1$
如果$det(R)<0$的时候选择第二大的值进行计算
$$Tr(MD)=d_1{M}_{11}+d_2{M}_{22}+d_3{M}_{33}$$
中$M_{11}=M_{22}=1，M_{33}=-1$
此时$$R=UC{V}^T$$
$$C=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& \mathrm{sign}\left(\det \left(U{V}^T\right)\right)\cdot 1\end{array}\right]$$

2 PCL中ICP算法的实现

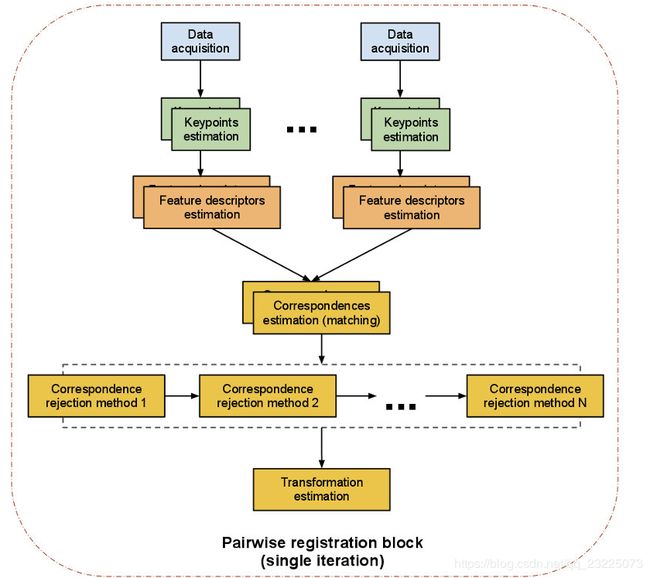
PCL中配准算法的标准流程，对于ICP来讲，输入是两团xyz点云，输出是source变换到target的刚体变换。其实核心求解过程都是上述公式，没啥可说的。在icp的实现里面默认是没有Reject bad correspondences这一步的

Iterative Closest Point Pipeline

• Search for correspondences（使用KdTree进行搜索最近点作为correspondent point）
• Reject bad correspondences（默认icp设置没有这一个）
• Estimate a transformation using the good correspondences（使用上述推导过程进行迭代式求解）
• Iterate（多次循环直到满足收敛条件）

关于上述推导公式的核心求解代码在pcl/registration/include/pcl/registration/impl/transformation_estimation_svd.hpp文件下的estimateRigidTransformation函数中，具体实现为

template <typename PointSource, typename PointTarget, typename Scalar> inline void
pcl::registration::TransformationEstimationSVD<PointSource, PointTarget, Scalar>::estimateRigidTransformation (
    ConstCloudIterator<PointSource>& source_it,
    ConstCloudIterator<PointTarget>& target_it,
    Matrix4 &transformation_matrix) const
{
  // Convert to Eigen format
  const int npts = static_cast <int> (source_it.size ());



  if (use_umeyama_)
  {
    Eigen::Matrix<Scalar, 3, Eigen::Dynamic> cloud_src (3, npts);
    Eigen::Matrix<Scalar, 3, Eigen::Dynamic> cloud_tgt (3, npts);

    for (int i = 0; i < npts; ++i)
    {
      cloud_src (0, i) = source_it->x;
      cloud_src (1, i) = source_it->y;
      cloud_src (2, i) = source_it->z;
      ++source_it;

      cloud_tgt (0, i) = target_it->x;
      cloud_tgt (1, i) = target_it->y;
      cloud_tgt (2, i) = target_it->z;
      ++target_it;
    }
    
    // Call Umeyama directly from Eigen (PCL patched version until Eigen is released)
    transformation_matrix = pcl::umeyama (cloud_src, cloud_tgt, false);
  }
  else
  {
    source_it.reset (); target_it.reset ();
    //  is the source dataset
    transformation_matrix.setIdentity ();

    Eigen::Matrix<Scalar, 4, 1> centroid_src, centroid_tgt;
    // Estimate the centroids of source, target
    compute3DCentroid (source_it, centroid_src);
    compute3DCentroid (target_it, centroid_tgt);
    source_it.reset (); target_it.reset ();

    // Subtract the centroids from source, target
    Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic> cloud_src_demean, cloud_tgt_demean;
    demeanPointCloud (source_it, centroid_src, cloud_src_demean);
    demeanPointCloud (target_it, centroid_tgt, cloud_tgt_demean);

    getTransformationFromCorrelation (cloud_src_demean, centroid_src, cloud_tgt_demean, centroid_tgt, transformation_matrix);
  }
}
// 求解方式1:（默认求解方式)
//////////////////////////////////////////////////////////////////////////////////////////
template <typename Derived, typename OtherDerived> 
typename Eigen::internal::umeyama_transform_matrix_type<Derived, OtherDerived>::type
pcl::umeyama (const Eigen::MatrixBase<Derived>& src, const Eigen::MatrixBase<OtherDerived>& dst, bool with_scaling)
{
  typedef typename Eigen::internal::umeyama_transform_matrix_type<Derived, OtherDerived>::type TransformationMatrixType;
  typedef typename Eigen::internal::traits<TransformationMatrixType>::Scalar Scalar;
  typedef typename Eigen::NumTraits<Scalar>::Real RealScalar;
  typedef typename Derived::Index Index;

  EIGEN_STATIC_ASSERT (!Eigen::NumTraits<Scalar>::IsComplex, NUMERIC_TYPE_MUST_BE_REAL)
  EIGEN_STATIC_ASSERT ((Eigen::internal::is_same<Scalar, typename Eigen::internal::traits<OtherDerived>::Scalar>::value),
    YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY)

  enum { Dimension = PCL_EIGEN_SIZE_MIN_PREFER_DYNAMIC (Derived::RowsAtCompileTime, OtherDerived::RowsAtCompileTime) };

  typedef Eigen::Matrix<Scalar, Dimension, 1> VectorType;
  typedef Eigen::Matrix<Scalar, Dimension, Dimension> MatrixType;
  typedef typename Eigen::internal::plain_matrix_type_row_major<Derived>::type RowMajorMatrixType;

  const Index m = src.rows (); // dimension
  const Index n = src.cols (); // number of measurements

  // required for demeaning ...
  const RealScalar one_over_n = 1 / static_cast<RealScalar> (n);

  // computation of mean
  const VectorType src_mean = src.rowwise ().sum () * one_over_n;
  const VectorType dst_mean = dst.rowwise ().sum () * one_over_n;

  // demeaning of src and dst points
  const RowMajorMatrixType src_demean = src.colwise () - src_mean;
  const RowMajorMatrixType dst_demean = dst.colwise () - dst_mean;

  // Eq. (36)-(37)
  const Scalar src_var = src_demean.rowwise ().squaredNorm ().sum () * one_over_n;

  // Eq. (38)
  const MatrixType sigma (one_over_n * dst_demean * src_demean.transpose ());

  Eigen::JacobiSVD<MatrixType> svd (sigma, Eigen::ComputeFullU | Eigen::ComputeFullV);

  // Initialize the resulting transformation with an identity matrix...
  TransformationMatrixType Rt = TransformationMatrixType::Identity (m + 1, m + 1);

  // Eq. (39)
  VectorType S = VectorType::Ones (m);
  if (sigma.determinant () < 0) 
    S (m - 1) = -1;

  // Eq. (40) and (43)
  const VectorType& d = svd.singularValues ();
  Index rank = 0; 
  for (Index i = 0; i < m; ++i) 
    if (!Eigen::internal::isMuchSmallerThan (d.coeff (i), d.coeff (0))) 
      ++rank;
  if (rank == m - 1) 
  {
    //如果三个值相差很大，判断UV行列式是否为+
    if (svd.matrixU ().determinant () * svd.matrixV ().determinant () > 0) 
      Rt.block (0, 0, m, m).noalias () = svd.matrixU () * svd.matrixV ().transpose ();
    else 
    {
      const Scalar s = S (m - 1); 
      S (m - 1) = -1;
      Rt.block (0, 0, m, m).noalias () = svd.matrixU () * S.asDiagonal () * svd.matrixV ().transpose ();
      S (m - 1) = s;
    }
  } 
  else 
  {
    Rt.block (0, 0, m, m).noalias () = svd.matrixU () * S.asDiagonal () * svd.matrixV ().transpose ();
  }

  // Eq. (42)
  if (with_scaling)
  {
    // Eq. (42)
    const Scalar c = 1 / src_var * svd.singularValues ().dot (S);

    // Eq. (41)
    Rt.col (m).head (m) = dst_mean;
    Rt.col (m).head (m).noalias () -= c * Rt.topLeftCorner (m, m) * src_mean;
    Rt.block (0, 0, m, m) *= c;
  }
  else
  {
    Rt.col (m).head (m) = dst_mean;
    Rt.col (m).head (m).noalias () -= Rt.topLeftCorner (m, m) * src_mean;
  }

  return (Rt);
}

// 求解方式2
///////////////////////////////////////////////////////////////////////////////////////////
template <typename PointSource, typename PointTarget, typename Scalar> void
pcl::registration::TransformationEstimationSVD<PointSource, PointTarget, Scalar>::getTransformationFromCorrelation (
    const Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic> &cloud_src_demean,
    const Eigen::Matrix<Scalar, 4, 1> &centroid_src,
    const Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic> &cloud_tgt_demean,
    const Eigen::Matrix<Scalar, 4, 1> &centroid_tgt,
    Matrix4 &transformation_matrix) const
{
  transformation_matrix.setIdentity ();

  // Assemble the correlation matrix H = source * target'
  Eigen::Matrix<Scalar, 3, 3> H = (cloud_src_demean * cloud_tgt_demean.transpose ()).topLeftCorner (3, 3);

  // Compute the Singular Value Decomposition
  Eigen::JacobiSVD<Eigen::Matrix<Scalar, 3, 3> > svd (H, Eigen::ComputeFullU | Eigen::ComputeFullV);
  Eigen::Matrix<Scalar, 3, 3> u = svd.matrixU ();
  Eigen::Matrix<Scalar, 3, 3> v = svd.matrixV ();

  // Compute R = V * U'
  if (u.determinant () * v.determinant () < 0)
  {
    for (int x = 0; x < 3; ++x)
      v (x, 2) *= -1;
  }

  Eigen::Matrix<Scalar, 3, 3> R = v * u.transpose ();

  // Return the correct transformation
  transformation_matrix.topLeftCorner (3, 3) = R;
  const Eigen::Matrix<Scalar, 3, 1> Rc (R * centroid_src.head (3));
  transformation_matrix.block (0, 3, 3, 1) = centroid_tgt.head (3) - Rc;
}