MATLAB不同时频信号处理方法介绍及效果对比
本文欢迎非商业目的的学习分享转载，转载请附上原文链接及作者ID
本文为作者自身的一个学习总结，大部分内容在相关教材上也可以找到，有空的也会不定期更新。本身也在学习的过程中，出现错误在所难免，欢迎大家在留言区指正。看到的话我都会及时回复的。
文章中使用的数据有需要的话可以从此处进行下载
目录
- MATLAB不同时频信号处理方法介绍及效果对比
- 1. 信号的频域分析
- 1.1 Fourier（FFT）变换基本原理
- MATLAB 中信号FFT的基本处理方法
- MATLAB 中不同参数设置对FFT结果的影响
- 1. 采样点数的影响
- 2. fft变换点数nfft对频率分辨率的影响
- 3. 窗函数对FFT变换效果的影响
- 4. 频谱细化技术（Zoom-FFT）
- 信号的功率谱分析的基本原理
- MATLAB中信号功率谱分析的基本方法
- 经典非参数法功率谱估计
- 1. 周期图法
- 2. 基于维纳辛钦定律（Wiener-Khintchine theorem）的相关法
- 3. 平滑周期法（Blackman-Tukey法）
- 4. 平均周期法 （Welch-Bartlett法）
- 5. 重叠平均周期法 （Welch法）
- 参数法功率图估计
- 2. 信号的时频分析
- 2.1 短时Fourier变换(Short Time Fourier Transform-STFT)
- 2.2 Gabor变换
- 2.3 Wigner-Ville变换
- 2.4 小波分析
- 2.5 Hilbert-Huang变换
- 模态分解的方法
- Hilbert谱和Hilbert边际谱
- EMD在MATLAB中的应用
- HHT变换
- 分数阶Fourier变换
- 其他一些问题说明
- 是否转换为dB显示？
- 主要参考文献
- 未完待续，持续更新中，欢迎大家指出相关问题，写到后面感觉前面突然一堆逻辑错误2333~
MATLAB不同时频信号处理方法介绍及效果对比
从大二到现在接触傅里叶变换已经好几年了，对傅里叶变换的基本概念与方法和使用的注意事项也都有所了解，但动手方面一直较为欠缺，最近刚好又重新在做相关方面的可以，顺手通过Matlab把整个信号的FFT和相关的时频概念都串起来复习一下，方便以后查找。
不同于一般教程中使用生成的函数进行分析，本文直接使用一段实际采集的电机径向的振动信号进行分析处理，更真实地符合现实情况
1. 信号的频域分析
1.1 Fourier（FFT）变换基本原理
傅里叶变换的基本公式基本上可以在任何一本有关信号处理的大学教材或者相关的培训PPT上找到，在这里不再赘述。而关于傅里叶变换究竟是什么，网上有很多通俗化的解释，看到的比较好的文章有知乎的一篇专栏:如果看了这篇文章你还不懂傅里叶变换，那就过来掐死我吧，另外b站上也有一个国外大神3Blue1Brown制作的一个可视化效果非常出众的短片:形象展示傅里叶变换。
傅里叶变换的可视化表示:
简单来说就是任何一个时域信号都可以用一系列正弦函数sin(nx)的和来表示，并且使用的正弦函数项越多，所得到的“模拟信号”也就更接近真实信号。信号的傅里叶变换实际上就是求这一系列正弦函数系数的过程。
至于为什么可以对一个信号进行傅里叶变换和为什么能这么对信号进行变换这个问题我一直到研一上完“矩阵分析”，和“数字信号处理”这么课之后才有了比较清楚的认识。无论是傅里叶变换，短时傅里叶变换，还是后面会谈到的小波变换，经验模态分解。其本质都是时域信号在线性空间正交基上的分解与重构，而信号分析的重点则在于如何针对不同的信号来选择相应合适的线性空间正交基，或者说各类变换的“核函数”
至于为什么学的时候教的都是傅里叶变换，而实际用的函数都是FFT（快速傅里叶变换），这是
MATLAB 中信号FFT的基本处理方法
在MATLAB中进行FFT的函数为fft（）
y=fft(x,n)
其中x为时域信号，参数n表示执行n点fft变换
下面举一个最简单的例子
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
nfft=2^12;%fft变换点数4096
x=fft_data(1:2^12);%取1秒不到的时域数据
fy=abs(fft(x,nfft));
fx=(1:nfft/2)*fs/nfft;
t=0:1/fs:nfft/fs-1/fs;
figure()
subplot(121)
plot(t,x);
xlabel('t/s');ylabel('幅值');title('原始时域信号')axis([0 nfft/fs -1 1])
subplot(122)
plot(fx,fy(1:nfft/2)*2/nfft);
xlabel('频率/Hz');ylabel('幅值');title('FFT频域信号');axis([0 fs/2 0 0.1])
toc
%时间已过 0.098931 秒
MATLAB 中不同参数设置对FFT结果的影响
1. 采样点数的影响
根据香农采样定律，若已知信号的最高频率为fc，为防止混叠，则选定抽样频率fs应该满足fs≥2fc，同时根据选定的频率分辨率f0，则确定进行FFT变换所需要的点数N=fs/f0=Tfs。
在采集信号的过程中，为了防止混叠，首先应选定抽样频率fc，但同时该频率不建议选得太高，否则为了实现理想的频域分辨率，N会变得很大。极大地增加FFT过程中的计算量。
现在对上述FFT程序做适当更改，比较当数据点数分别等于2048，4096和8192时FFT的变换结果。
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
nfft=[2^11 2^12 2^13];%fft变换点数2048,4096,8192
ndata=[2^11 2^12 2^13];%数据量，取1秒,2秒，3秒左右的数据
x1=fft_data(2^12:ndata(1)+4095);fy1=abs(fft(x1,nfft(1)));fx1=[(1:nfft(1)/2)*fs/nfft(1)];
x2=fft_data(2^12:ndata(2)+4095);fy2=abs(fft(x2,nfft(2)));fx2=[(1:nfft(2)/2)*fs/nfft(2)];
x3=fft_data(2^12:ndata(3)+4095);fy3=abs(fft(x3,nfft(3)));fx3=[(1:nfft(3)/2)*fs/nfft(3)];
figure()
plot(fx1,fy1(1:nfft(1)/2)*2/nfft(1),'-r',...
fx2,fy2(1:nfft(2)/2)*2/nfft(2),'-b',...
fx3,fy3(1:nfft(3)/2)*2/nfft(3),'-g');
xlabel('频率/Hz');ylabel('幅值');title('FFT频域信号');axis([0 fs/2 0 0.1])
legend('2048','4096','8192');
toc
从结果中切实可以比较清楚的看出频率分辨率随着处理点数的增加而增加了，原始信号为30Hz的振动信号，当采样频率增加之后，原本被淹没掉的谐波分量也显示了出来。
但是需要注意的是，当采样时间较长时，系统状态可能发生改变，虽然频谱“分辨率”提高了，但是又重新引入了不少杂质分量，因此不一定能够提高频率的分辨率
2. fft变换点数nfft对频率分辨率的影响
在MATLAB中fft函数的基本形式是y=fft(x,n)，其中n为fft变换的点数，一般来说为了提高fft计算的效率，n都会选择一个2的整数次幂的数值，这里假定该数值为nfft，信号x时域数据中点点数为N。一般来说为了不浪费时域在MATLAB中fft函数的基本形式是y=fft(x,n)，其中n为fft变换的点数，一般来说为了提高fft计算的效率，n都会选择一个2的整数次幂的数值，这里假定该数值为nfft，信号x时域数据中点点数为N。一般来说为了不浪费时域中的信息，nfft≥N，多出来的点数用0补足，这个操作我们称之为补零（zero padding）。
在前面有说过频谱的分辨率f0=fs/nfft，nfft为进行fft变换的点数，当我们进行补零操作后，参与fft变换的点数有N变为nfft，变大了，看起来频谱的分辨率f0增加了，我们在没有增加数据量的情况下提高了频谱的分辨率，上述说法是不准确的。
这里有两个概念需要说明，一个是物理分辨率，一个是计算分辨率。
物理分辨率：f0=1/T Hz，只和采样时间有关
计算分辨率：f0=fs/nfft Hz，和fft变换点数有关
这里借用一篇文章中的几幅图片对这个概念进行一下说明。下面第一幅图是原始数据图像，第二幅图是补零后的数据图像。
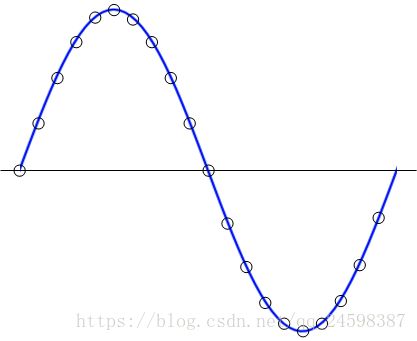
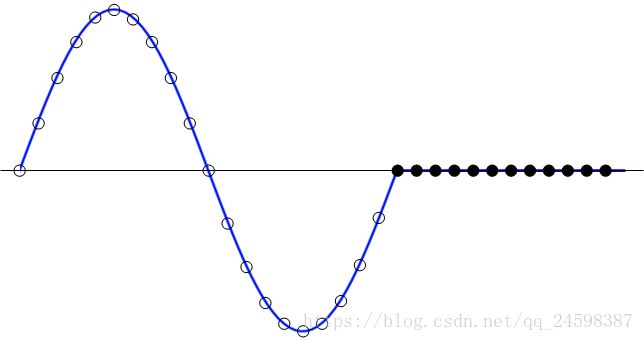对比两幅图片，其实可以发现补零后的fft的分析对象发生了改变。我们知道实际信号一般是无限长序列，而FFT针对的序列总是有限长度的，因此，DFT假设实际信号为对输入的有限长序列信号的周期延拓。将上面两幅图分别进行周期延拓之后，可以得到下面的周期序列。
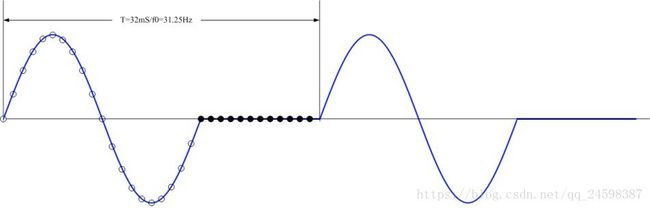
对比上面两幅图，其实可以看到对于同样长度的分析数据，通过补零得到的数据可以看做对原始数据加窗后得到的数据。而对数据加窗就会在频域上产生频谱泄露，这也就解释了为什么补零能提高频域的分辨率，但却无法提供更多的信息
下面在举一个例子来说明这个问题，以256Hz的采样率对70Hz的正弦波采集1s的数据，并对该段数据做FFT变换，可以得到下列图像，可以看到FFT准确地描述了原始信号的频谱分量。
当我们队原始信号进行补零操作后，观察得到的FFT图像如下。可以非常明显的看到频谱泄露的现象。当我们把70Hz附近的图像放大之后，可以看到原本的谱线变成了类似于sinc（f）的形式。这也就印证了前面印证前面加窗的说法。因为时域上的加窗等于频域上的卷积，而矩形窗FFT的结果就是一个sinc（）函数。
对于上述问题有一种解决方案是用本身的数据代替零点来补足缺少的问题，这种方法也存在一些问题，这里不做讨论，而是介绍另外一种加窗的操作方法。通过对补零后的数据添加类似hann（hanning窗）等窗函数，来减小频率泄露的问题。这样做的原因是时域加窗等于频域上的卷积，而合适的窗函数在频域上的能量较为集中，频谱泄露的情况也能有所减轻。但加窗又会出现一些其他的问题，可以参考我的另外一边文章《
FFT快速傅里叶变换中的误差来源》
最后我们来看一下不同补零形式所体现的效果。从上到下分别是未补零，直接补零和加窗补零。
最后还是通过MATLAB来实践一下不同nfft点数的FFT处理效果。
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
nfft=[2^11 2^12];%fft变换点数2048,4096,8192
ndata=[2^11 2^12];%数据量，取1秒,2秒，3秒左右的数据，4秒左右的数据
x1=fft_data(1:ndata(1));fy1=abs(fft(x1,nfft(1)));fx1=[(1:nfft(1)/2)*fs/nfft(1)];
x2=fft_data(1:ndata(1));fy2=abs(fft(x2,nfft(2)));fx2=[(1:nfft(2)/2)*fs/nfft(2)];
x3=fft_data(1:ndata(1)).*hann(2^11);fy3=abs(fft(x3,nfft(2)));fx3=[(1:nfft(2)/2)*fs/nfft(2)];
x4=fft_data(1:ndata(2));fy4=abs(fft(x4,nfft(2)));fx4=[(1:nfft(2)/2)*fs/nfft(2)];
figure(1)
plot(fx1,fy1(1:nfft(1)/2)*2/nfft(1),'-r',...
fx2,fy2(1:nfft(2)/2)*2/nfft(2),'-b',...
fx3,fy3(1:nfft(2)/2)*2/nfft(2),'-g',...
fx4,fy4(1:nfft(2)/2)*2/nfft(2),'-c');
xlabel('频率/Hz');ylabel('幅值');title('FFT频域信号');axis([0 fs/2 0 0.1])
legend('未补零','直接补零','加窗补零','增加采样点');
figure(2)
t2=0:1/fs:4095/fs;
plot(t2,x4,':b',t2,[x3;zeros(2048,1)],'-r',t2,[hann(2048);zeros(2048,1)],'-g');
xlabel('时间/s');ylabel('幅值');title('时域信号');
%axis([0 fs/2 0 0.1])
legend('原始两倍信号','加窗后的补零信号','hanning窗');
toc
通过观察上述fft处理后的图像可以发现，与原始信号相比，直接补零虽然看似提高了频域的分辨率，但也造成了较明显的频谱泄露现象。而如果以增加FFT点数后的FFT变换效果为参考，加窗补零这种方法不仅在一定程度上提高了频谱的分辨率，而且与直接补零相比还叫好地抑制了频谱泄露的现象。
说了这么久补零的局限性，最后简单说一下补零的优点：除了上述提到的（1）使得数据长为2的整数次幂以提高FFT的算法外（2）克服栅栏效应，是谱的外观得到平滑，提高谱的分析进度。
这里盗一张我们老师的课程PPT来进行说明，虽然补零并不能真正地提高频率分辨率，但是在非正周期采样的过程中，但是通过合理的补零可以对连续谱的谱峰值进行有效地逼近。
3. 窗函数对FFT变换效果的影响
这一小节主要对窗函数对作用进行分析，在进行数字信号处理时，不可能对无限长（完整）信号进行测量和运算，只能取有限的时间片段进行分析，这个过程称为信号截断，时域上的截断等于给原始信号乘上一个窗函数。而时域上两个函数相乘，在频域就是其频谱的卷积。由于窗函数不可能无限宽，其频谱不可能为冲激励函数，信号的频谱与窗函数的卷积必然产生拖尾现象，造成频谱泄露。原始谱线的能量因为与窗函数的卷积被分散到了两个较宽的频带当中，造成了能量泄露
频谱泄漏是由FFT算法中的一个假设导致的，即持续精确地重复时间记录，且时间记录中包含的信号在对应时间记录长度的间隔内呈周期性。若时间记录的周期数为非整数， 便违反该假设，导致频谱泄漏。另一种看法是，信号的非整数周期频率分量未与频谱频率线之一精确吻合。
您仅可在两种情况下保证获得整数周期。第一种情况是，您对测量的信号进行同步采样，因此可按需获取整数周期。
另一种情况是，您捕获的瞬时信号可完全融入时间记录。但是，多数情况下，您测量的未知信号是平稳的，即该信号在采集前、中、后都存在。这时，您就无法保证采样的是整数周期。频谱泄漏对测量造成干扰，来自给定频率分量的能量将分散至相邻的频率线或仓。您可使用窗口，将在非整数周期内进行FFT产生的效果最小化。
以矩形窗为例，有限宽度的矩形窗在频谱中的图像为sinc()函数。主瓣的宽度会随着N采样点数的增加而减小，从而降低频域卷积过程中造成的能量泄露。
N = 8; xn = ones(1,N);
Nfft = 8192 %较密的谱线近似连续谱
w = [-pi:2*pi/Nfft:(pi-2*pi/Nfft)];
Xk = fft(xn,Nfft);
figure
plot(w,abs(fftshift(Xk)))
因为在进行FFT的过程中，时域的截断是必然的，因此频域泄露也是必然的。因此只能想办法来减少截断过程中造成的频域泄露现象。主要有以下两种方法:（1）加大窗口宽度，既增加采样点数N；（2）采用适当的窗函数进行截断；
那什么是适当的窗函数呢?，一般认为窗函数的主瓣宽度应该尽可能的小，以提高频率分辨率，同时主瓣和第一旁瓣的幅值差值应该尽可能的大，并且旁瓣的衰减越快越好，从而减小频谱泄露提高频谱幅值精度。
但“鱼和熊掌不可兼得”的朴素真理在这里同样适用，主瓣宽度与旁瓣的幅度的衰减速度相互制约。主瓣宽度越小，频率分辨率越高，但旁瓣幅值较大，频谱泄露增加导致频谱精度降低，反之亦然。
如果仅仅需要求精确获得信号频率，而不考虑幅值精度，例如在进行固有频率测量的时候，就可以选择主瓣较窄的矩形窗。而如果在分析带有较强的干扰噪声的窄带信号的过程中，则应该选择旁瓣幅度较小的汉宁窗，三角窗等。在实际选择窗函数的过程中，需要对各个因素进行权衡处理。下图为各个窗函数的时域和频域波形，主瓣越大的窗，旁瓣衰减越快。
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
nfft=[2^12 2^13];%fft变换点数4096,8192
ndata=[2^12 2^13];%数据量，取1秒,2秒，3秒左右的数据，4秒左右的数据
x1=fft_data(1:ndata(1));fy1=abs(fft(x1,nfft(1)));fx1=[(1:nfft(1)/2)*fs/nfft(1)];
x2=fft_data(1:ndata(1)).*hann(ndata(1));fy2=abs(fft(x2,nfft(1)));fx2=[(1:nfft(1)/2)*fs/nfft(1)];
x3=fft_data(1:ndata(1)).*blackman(ndata(1));fy3=abs(fft(x3,nfft(1)));fx3=[(1:nfft(1)/2)*fs/nfft(1)];
x4=fft_data(1:ndata(1)).*gausswin(ndata(1));fy4=abs(fft(x4,nfft(1)));fx4=[(1:nfft(1)/2)*fs/nfft(1)];
x5=fft_data(1:ndata(2));fy5=abs(fft(x5,nfft(2)));fx5=[(1:nfft(2)/2)*fs/nfft(2)];
figure(1)
plot(fx1,fy1(1:nfft(1)/2)*2/nfft(1),'-r',...
fx2,fy2(1:nfft(1)/2)*2/nfft(1),'-b',...
fx3,fy3(1:nfft(1)/2)*2/nfft(1),'-g',...
fx4,fy4(1:nfft(1)/2)*2/nfft(1),'-m',...
fx5,fy5(1:nfft(2)/2)*2/nfft(2),'-c');
xlabel('频率/Hz');ylabel('幅值');title('FFT频域信号');axis([0 fs/2 0 0.1])
legend('矩形窗','Hanning Window','Blackman Window','Gassian Window','两倍矩形窗');
toc
通过对实际信号进行分析可以发现对于实际信号来说，与不加窗（也可以说是加矩形窗）的频谱相比，加了窗的频谱相对而言较为接近，由于主板较宽，频谱泄露因此频谱较为平缓，部分谐波分量被淹没。
4. 频谱细化技术（Zoom-FFT）
频谱细化指的是在频谱分析的过程中增加频谱中某个频率分辨率的方法，如果我们希望将频段[f1 ~ f2]内的频率分辨率提高K倍，最简单的方法就是在采样频率不变的情况下，将采样点数从N点增加到KN点，但这么做的过程中也同时将许多不感兴趣的频率分辨率也提高了，造成了算力的浪费。
重采样的基本原理如上，在进行细化分析的过程中，必须保证原始信号有足够的长度，如果想把频段的分辨率提高K倍，就得保证原信号的采样长度为KN，这样在每隔K点重采样的过程后，得到新长度为N的复序列，频谱细化技术实际上一种降低计算量的方法，而不是直接使用原始数据来提高频率分辨率的方法。
下面通过代码具体分析频谱细化的具体作用：
此部分暂时无法实现，后续进行内容补充
信号的功率谱分析的基本原理
有很长的一段时间内我都混淆了信号的FFT谱与功率谱之间的概念，关于信号的FFT和功率谱可以参考我博客中的两篇文章：《功率谱和频谱的区别、联系》和《功率谱估计》。对功率谱与FFT的基本概念有了比较准地说明。
从个人的角度理解，从名字就能看出这两者的主要区别：“FFT-快速傅里叶变换”，“功率谱估计”。FFT本质上是一个对信号分解的过程，以一种工具。而“功率谱估计”则更侧重估计二字，功率谱估计的出发点就是将分析的对象看做是随机信号，希望通过各种方法来准确地通过采样信号准确地估计出真实信号在频谱上的功率分布，而FFT则是假定分析的对象是一个“确定性的周期信号”来直接对其分解，求解相关的系数。
而在FFT分析的过程中，为了准确描述信号频谱而采取的类似加窗的操作，个人也有几分估计的味道在里面，并且这种“估计”的操作在功率谱估计的过程中也经常能够看到。同时功率谱估计过程中使用的类似平均等手段个人感觉也可以用在FFT上，但目前这些手段主要还是运用在功率谱估计上，暂时不清楚为何，姑且追寻主流使用这种方法吧。
对于随机信号x(n)来说，实际工作中我们只能得到有限长度N的数据，要由这N个数据来估计信号的均值，方差，自相关函数，功率谱等其他感兴趣的参数。作为一个估计量，我们就需要评价这个估计量的质量，一般的评价手段有偏差，方差，均方差等几个角度。
经典的非参数功率谱估计方法无法同时在偏差，方差等几个角度达到非常理想的估计效果，这也是现代的功率谱估计方法引入参数法功率估计的原因。从这个角度也可以看出功率谱估计和FFT之间的一个显著的区别，我们对信号进行FFT后一般情况下并不会非常在意FFT是否非常准确地还原了原始信号，而是主要关注了FFT频谱中的主要分量，而在使用功率谱估计的过程中，则会较多地关注相关方法的“准确程度”
关于功率谱估计的质量的具体数学推导过程可以参考比较早的一篇博文《功率谱估计》，在这里不详细描述，只是简单提一下相关的结果。
MATLAB中信号功率谱分析的基本方法
经典非参数法功率谱估计
1. 周期图法
定义：计算随机信号x(n)的N点观察数据的DFT，然后取其幅值的平方并除以N作为对x(n)真实功率谱的估计
对于这种方法来说，周期图法估计的方差不随采样点数N的增加而减小。不是功率谱的一致估计，而当N趋向无穷时，变差逐渐趋近于零，是真实值的渐进无偏估计。
%直接编程
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
Nfft=8192;
x1=fft_data(1:Nfft);
fy1=abs(fft(x1))/length(x1);
Pxx=2*fy1.^2;
index=0:round(Nfft/2-1);
w=index*fs/Nfft;
figure
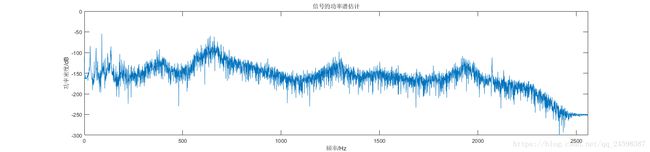
plot(w,10*log(Pxx(index+1)))
xlabel('频率/Hz');ylabel('功率密度/dB');title('信号的功率谱估计');axis([0 2560 -300 0]);
toc
%使用MATLAB官方函数
clear;clc;
tic
load('vibdata.mat')
fs=5120;%实际采样频率
Nfft=4096;
x1=fft_data(1:4096);
[Pww,F,pxxc]=periodogram(x1,[],[],fs,'ConfidenceLevel',0.95);
figure
plot(F,10*log(Pww),F,10*log(pxxc),'-.')
xlabel('频率/Hz');ylabel('功率密度dB/Hz');title('95%置信区间的信号的功率谱估计');axis([0 fs/2 -300 0]);
toc
这里有一部分问题就是，在计算的过程中，仔细对比两幅图像，可以发现虽然整体形状一致，但手动编程与直接使用MATLAB函数相比，产生PSD整体偏大，该问题暂时自己没法解释，进行搁置
2. 基于维纳辛钦定律（Wiener-Khintchine theorem）的相关法
定义：信号的功率谱估计等于该信号自相关函数的离散DTFT（离散时间傅里叶变换） 同时对于平稳随机过程来说，信号的自相关函数就是功率谱密度函数的逆傅里叶变换，而对于非平稳随机过程来说，功率谱密度的逆变换的结果是自想换函数在时域上的平均。
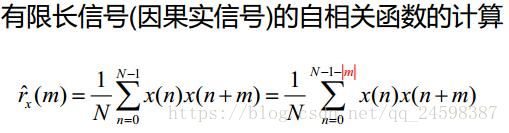
对于相关法来说，当时延m取值的最大值为N-1时，相关法和周期法等效。随着m取值的增大，相关法功率谱估计质量的方差特性和周期图法功率谱估计会具有一样的缺点。
3. 平滑周期法（Blackman-Tukey法）
为了降低估计的方差，可以对自相关函数的估计值进行加窗后再进行FFT变换，可以证明这种方法的方差要小于原始的相关法，但这种方法同时也降低了频率的分辨率。
4. 平均周期法 （Welch-Bartlett法）
这种方法是将随机序列分为L段，分别求每一段的周期图，最后再进行平均。可以证明当L趋于无穷时，方差趋向于0，是一致估计。但平均图方差减小的代价就是偏差增大。这种方法减小方差的同时也降低了谱的分辨率。主要原因是分段即加窗，窗越短，主瓣宽度越大。
5. 重叠平均周期法 （Welch法）
与平均周期法相比，这种方法将各段数据进行了一定的重叠
在MATLAB中，Bartlett法和Welch法都可以用pwelch函数进行操作。关于pwelch函数的使用方法既可以直接参考MATLAB官方文档，也可以参考我博客中的文章《MATLAB中应用pwelch（）函数实现功率谱估计》
对于几种方法，如果采用一个已知信号进行对比，可以发现：
- 周期图法谱估计曲线的波动很大，即估计的方差较大
- Welch 法谱估计曲线较为光滑，方差减小，但分辨率降低
- 对于Welch 法，当数据分段增加时，各段数据较短时，谱的分辨率明显下降，而谱估计曲线较为光滑，方差较小；反之当数据分段数减小，各段数据较长时，谱分辨率明显提高，而谱估计曲线波动较大，方差较大
下面采用以一段已知信号来演示各种功率谱估计方法和FFT变换之间的区别：
clear;clc;
tic
fs=1024;
T=4;
t=(0:T*fs-1)/fs;
x=0.1*cos(2*pi*4*t)+0.1*cos(2*pi*4.5*t)+rand(1,size(t,2));
Nfft=2^nextpow2(size(x,2));
%FFT变换
ffy1=abs(fft(x))/Nfft;
fy1=ffy1(1:Nfft/2+1);
fy1(2:end-1)=2*fy1(2:end-1);
fx1=(0:Nfft/2)/Nfft*fs;
figure
subplot(3,1,1)
plot(fx1,20*log(fy1));
xlabel('频率/Hz');ylabel('FFT变换幅值/dB');title('信号的FFT变换');axis([0 80 -200 50]);
%Welch法功率谱估计
[pxx1,w1]=pwelch(x,[],[],[],fs);
subplot(3,1,2)
plot(w1,10*log(pxx1))
xlabel('频率/Hz');ylabel('功率密度/dB');title('信号的Welch法功率谱估计');axis([0 80 -200 50]);
%周期图法
[pxx2,w2] = periodogram(x,[],[],fs);
subplot(3,1,3)
plot(w2,10*log(pxx2))
xlabel(
前边谈到Welch法和周期图法的特点在上图中都有比较明显的体现，同时可以发现如果通过对比可以发现如果将FFT变换的频谱用指数形式表示，则最后的结果和周期图法得到的变换结果相一致，关于这一点相信大家也并不会意外。
参数法功率图估计
2. 信号的时频分析
对于普通的FFT变换来说，其能够
- 准确地反映信号所包含的频率分量，不能反映频率分量存在的时间段
- 能反映调频信号的频率范围，不能反映频率随时间的变化规律
- 能准确反映信号中某频率分量的总能量，缺不能显示频率分量强度强度随时间的变化功率
简单地来说FFT是一种全局变换，在变换的过程中把整个信号的能量给平均了。我们知道FFT(x1+X2)=FFT(X1)+FFT(X2)，傅里叶变换是满足线性性质的。如下图所示，对于信号1,2来说，这两个信号的FFT频谱一致，但信号而的余弦分量和信号1相比，以两倍的幅值出现了1半的时间。该谐波分量的总能量及平均幅值一样，故在FFT频谱上显示的幅值一致。
对于平稳信号来说，FFT这么分析没有什么问题，但对于非平稳信号来说，如果想分辨1、2两种情况，仅仅用FFT变换就无法解决问题了，这时就需要借助这一节中需要将到的各类视频分析方法。
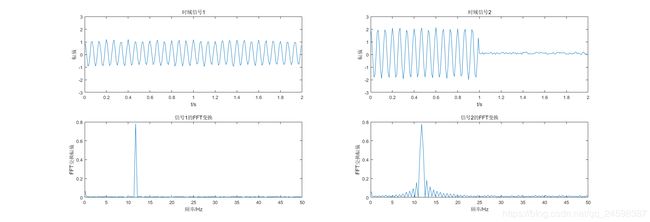
clear;clc;
tic
fs=100;
T1=2;
t1=(0:T1*fs-1)/fs;
x1=cos(2*pi*15*t1)+0.2*rand(1,size(t1,2));
T2=1;
t2=(0:T2*fs-1)/fs;
x2=2*cos(2*pi*15*t2)+0.2*rand(1,size(t2,2));
x2=[x2,0.2*rand(1,size(t2,2))];
Nfft=2^nextpow2(size(x1,2));
%FFT变换
ffy1=abs(fft(x1))/Nfft;
fy1=ffy1(1:Nfft/2+1);
fy1(2:end-1)=2*fy1(2:end-1);
fx1=(0:Nfft/2)/Nfft*fs;
ffy2=abs(fft(x2))/Nfft;
fy2=ffy2(1:Nfft/2+1);
fy2(2:end-1)=2*fy2(2:end-1);
fx2=(0:Nfft/2)/Nfft*fs;
%画图
figure
subplot(2,2,1)
plot(t1,x1);
xlabel('t/s');ylabel('幅值');title('时域信号1');axis([0,2,-3,3]);
subplot(2,2,2)
plot(t1,x2);
xlabel('t/s');ylabel('幅值');title('时域信号2');axis([0,2,-3,3]);
%FFT变换结果
subplot(2,2,3)
plot(fx1,fy1);
xlabel('频率/Hz');ylabel('FFT变换幅值');title('信号1的FFT变换');
subplot(2,2,4)
plot(fx2,fy2);
xlabel('频率/Hz');ylabel('FFT变换幅值');title('信号2的FFT变换');
toc
2.1 短时Fourier变换(Short Time Fourier Transform-STFT)
STFT个人认为是其与传统的傅里叶变换之间并没有非常显著的区别。其本质上就是一个加窗的傅里叶变换，通过窗函数的移动来获取不同时间内的频率分量。傅里叶变换中拥有的性质基本上都可以直接移植到STFT上来。对于STFT来说，如果将窗口选得非常小，虽然时域上的分辨率非常高，但是由于时间太短，频域上的分辨率非常低。而如果窗口选得非常大的话，又变成了最原始的加窗傅里叶变换，时间上的分辨率非常低。时域和频域上的分辨率不可兼得。时域分辨率和频域分辨率的乘积是一个定值。
在MATLAB中，官方给出的短时傅里叶变化你的函数为spectrogram,这里参考一篇博客和mathworks的官方文档，对该函数进行学习说明，该函数的用法为：
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
在不给出左侧返回值的情况下，该函数直接生成使用短时傅里叶变换得到的频谱图。现对默认参数进行说明：
- x-输入信号向量，默认被平分为8段，不能平分的话进行截断
- window-若window为整数，则使用改长度的Hamming窗，若为向量，使用每段指定长度的窗函数
- noverlap-各段之间重叠的采样点数，需要为小于window的整数
- Nfft-进行离散傅里叶变换的点数
- fs-采样频率，不指定的话默认为1hz
- S-输入信号x的短时傅里叶变换，每一列包含一个短时局部时间的频率成分估计，时间沿列增加，频率沿行增加
- F-??
- T-频谱图计算的时刻点
- P-能量谱密度？？？
对于输入参数来说，nfft越大，频域的分辨率就越高，但时间的分辨率就越差，而noverlap影响时间轴分辨率，越大的话，时间分辨率越高
下面使用一个具体的实例
%计算并显示二次扫频信号的PSD图，扫频信号的频率开始于100Hz，在1s时经过200Hz
T = 0:0.001:2;
X = chirp(T,100,1,200,'q');
figure()
subplot(2,2,1);
spectrogram(X,512,480,1024,1E3,'yaxis');
title('512-Window-480-Overlap');
subplot(2,2,2);
spectrogram(X,512,120,1024,1E3,'yaxis');
title('512-Window-120-Overlap');
subplot(2,2,3);
spectrogram(X,128,120,1024,1E3,'yaxis');
title('128-Window-120-Overlap');
subplot(2,2,4);
spectrogram(X,128,10,1024,1E3,'yaxis');
title('128-Window-10-Overlap');
从上面的对比中可以很明显的看出，当重叠较小的频谱在时域上看起来比较连续，但值得注意的是，由于这里频率变换比较快，且在指定时间频率成分较为单一，当窗函数较大时，指定窗函数内的频率成分较为多样，频率分辨率反而较低，需要根据具体的情况进行分辨。
现使用实际数据来进行分析，取半个周期的数据
clear;clc;
%电机数据均为15Hz，内部负载为80load，采样率为5120Hz，取1个周期的数据
%由于频率过高，进行降采样，频率为1280Hz，采样点为1280
load('normal.mat');
normal=data(1:4:5120*4,5);
load('bowed.mat');
bowed=data(1:4:5120*4,5);
load('bearing.mat');
bearing=data(1:4:5120*4,5);
load('broken.mat');
broken=data(1:4:5120*4,5);
window=256;
noverlap=200;
nfft=2048;
figure()
subplot(2,2,1);
spectrogram(normal,window,noverlap,nfft,5120,'yaxis');
title('normal');
subplot(2,2,2);
spectrogram(broken,window,noverlap,nfft,5120,'yaxis');
title('broken bar');
subplot(2,2,3);
spectrogram(bowed,window,noverlap,nfft,5120,'yaxis');
title('bent rotor');
subplot(2,2,4);
spectrogram(bearing,window,noverlap,nfft,5120,'yaxis');
title('bearing');
2.2 Gabor变换
2.3 Wigner-Ville变换
2.4 小波分析
《连续小波变换、离散小波变换、二进小波变换、离散序列的小波变换、小波包》《有关小波的几个术语及常见的小波基介绍》
简单总结：
- 连续小波变换
就是，小波变换最常见到的公式和形式就是连续小波变换，公式如下：
W f ( a , b ) = 1 ∣ α ∣ ∫ − ∞ ∞ f ( t ) Ψ ( t − b a ) d t W _ { f } ( a , b ) = \frac { 1 } { \sqrt { | \alpha | } } \int _ { - \infty } ^ { \infty } f ( t ) \Psi \left( \frac { t - b } { a } \right) \mathrm { d } t Wf(a,b)=∣α∣1∫−∞∞f(t)Ψ(at−b)dt
式子中a代表尺度（在某种意义上就是频率的概念），b是时间参数或者平移参数。不严谨的说 W f ( a , b ) W _ { f } ( a , b ) Wf(a,b)值得是对信号进行小波变换后当频率为a时间为b时的值，可以看出一维信号进过变换后成为了二维信号。- 离散小波变换
离散小波变换DWT指的是将CWT中的尺度参数a和平移参数b离散化，而没有将信号和小波中的时间变量t离散化。
在对尺度参数a和平移参数b离散的过程汇总，一般对尺度进行幂级数离散化，令 a = a 0 m a = a _ { 0 } ^ { m } a=a0m，对b进行均匀离散化，考虑到不同尺度下频率不同，因此不同尺度下参数b的离散间隔不同- 二进小波变换（Dyadic Wavelet Transform）
在二进小波变换汇总，取特殊化，令 a 0 = 2 a_{0}=2 a0=2，然后保持平移参数b仍是连续的，则这类小波被称为二进小波变换。- 离散序列的小波变换
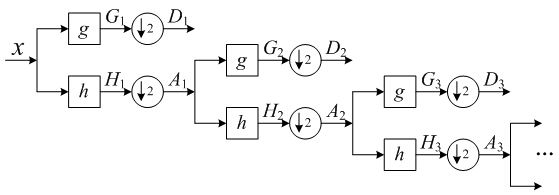
上面说的三种小波变换的小波基都不是正交基，会带来一些麻烦，通过他们对信号进行变换后的信息是有冗余的，Mallat给出了一种在正交小波基上的信号分解算法，就是著名的Mallat算法。
离散序列的小波变换就是基于Mallat算法，在分解的过程汇总，初始系数x（暂且这么称呼）与其第一层分解后的高频系数D1（细节部分Detail）的关系是x经过高通滤波器g滤波后再下采样，与低频系数A1（近似部分Approximate）的关系是x经过低通滤波器h滤波后再下采样；然后继续对低频系数A1进行第二层分解，低频系数A1与其第二层分解后的高频系数D2（细节部分Detail）的关系是A1经过高通滤波器g滤波后再下采样，与低频系数A1（近似部分Approximate）的关系是A1经过低通滤波器h滤波后再下采样；后面依次类推即可。由于一直在下采样，所以虽然滤波器系数g和h不变，但其滤波带宽一直在减半。初始系数是怎么来的呢？肯定是根据信号得到的，最简单最粗糙的办法就是对信号直接抽样。这是对连续信号进行正交小波分解，有了这些系数，再利用正交小波基，就可以表示出信号了，这类似于连续周期信号的傅里叶级数分解吧。
- 小波包
无论是低频系数还是高频系统都进行同样的分解，然后选取一个最合适的分解路径。怎么评价分解是否是最优的呢？最自然的想法就是利益最大化或者是代价最小化，构建一个代价函数求一下看看如分解代价最小。代价函数有很多种，具体不说了。
接下来使用MATLAB中的具体函数来对信号进行小波分解。
这部分的内容较多，另外单独写了一篇文章MATLAB小波变换工具箱 Wavelet Toolbox 实际操作与训练，可以进行相关的查阅。
不过小波变换虽然有诸多优点，但是小波变换始终受到小波基函数的影响，且一直没有非常合适的小波及选取理论，导致小波变换在信号处理的过程中无法实现对信号的自适应变换。
2.5 Hilbert-Huang变换
关于这部分内容可以参考一篇文章HHT变换讲义，个人觉得说的非常清楚，通俗易懂
Hilbert-Huang变换，即HHT是一种用于处理不平衡，无规律数据的存在滋生调整型的数据处理方式。
HHT主要内容包含两部分，第一部分为经验模态分解（Empirical Mode Decomposition，简称EMD），它是由Huang提出的；第二部分为Hilbert谱分析（Hilbert Spectrum Analysis，简称HSA）。简单说来，HHT处理非平稳信号的基本过程是：首先利用EMD方法将给定的信号分解为若干固有模态函数（以Intrinsic Mode Function或IMF表示，也称作本征模态函数），这些IMF是满足一定条件的分量；然后，对每一个IMF进行Hilbert变换，得到相应的Hilbert谱，即将每个IMF表示在联合的时频域中；最后，汇总所有IMF的Hilbert谱就会得到原始信号的Hilbert谱。
在HHT中，IMF应该具有以下两条性质：
- 极值总数与过零总数最多相差1
- 上包络线和下包络线的均值必须是零
模态分解的方法
1.采用样条差值方法将x（t）的所有极大值点连线E1和极小值点连线E2，及平均包络线p（t）
2.y(t)=x(t)-p(t)，检查y是否满足IMF的性质，如果不满足的话反复操作，直到获得满足IMF性质的c（t）=y（t）作为x（t）的第1个IMF分量IMF1
3.x-c得到全新的x，再重复1,2得到下一个IMF，直到满足规定要求后停止，x就能表示成为IMF和残差量q(t)的和
x ( t ) = ∑ i = 1 m c i ( t ) + q ( t ) x ( t ) = \sum _ { i = 1 } ^ { m } c _ { i } ( t ) + q ( t ) x(t)=∑i=1mci(t)+q(t)
Hilbert谱和Hilbert边际谱
设序列x的Hilbert变换y为：
y ( t ) = 1 π ∫ − ∞ ∞ x ( τ ) t − τ d τ = x ( t ) ∗ 1 π t y ( t ) = \frac { 1 } { \pi } \int _ { - \infty } ^ { \infty } \frac { x ( \tau ) } { t - \tau } d \tau = x ( t ) * \frac { 1 } { \pi t } y(t)=π1∫−∞∞t−τx(τ)dτ=x(t)∗πt1
Hilbert变换的频率响应为
H ( j ω ) = − sign ( ω ) = { − j , ω ≥ 0 j , ω < 0 H ( j \omega ) = - \operatorname { sign } ( \omega ) = \left\{ \begin{array} { c } { - j , \omega \geq 0 } \\ { j , \omega < 0 } \end{array} \right. H(jω)=−sign(ω)={−j,ω≥0j,ω<0，
信号幅值没有变化，主要是改变了信号相位
EMD在MATLAB中的应用
早期的Matlab并没有HHT，EMD等内置函数，需要下载第三方的工具箱，或者自信编写相关的函数，而在R2018b的版本以后，MATLAB中已经有了相关的原生函数
MATLAB中进行EMD分解的方法是：
- [imf,residual,info] = emd(X,‘Interpolation’,‘pchip’);
这种方法对信号进行EMD分解，并返回得到的固有模态函数IMF，残差量residual和分解过程中保存的信息info
- emd(X,‘Interpolation’,‘pchip’);
如果没有左边参数，函数会直接返回直接画出原始信号，前三个IMF和残差量
- 参数说明：
emd函数中可以对EMD分解过程的中的一些参数进行设置，如停止方式，可以选择最大迭代次数，误差收敛方式，最大IMF数量，等，具体可以参考Mathworks的官方文档。但Interpolation这个参数比较常用，需要注意， 如果信号x是光滑信号，应该选择spline,样条曲线，而如果信号x是非光滑的信号，则应该选择pchip，使用分段三次Hermite插值多项式方法进行连接。
HHT变换
对随机序列x(t)j进行希尔伯特变换之后得到y(t)，由x,y可以得到一个解析信号z(t)
Z ( t ) = X ( t ) + i Y ( t ) = a ( t ) e i θ ( τ ) Z ( t ) = X ( t ) + i Y ( t ) = a ( t ) e ^ { i \theta ( \tau ) } Z(t)=X(t)+iY(t)=a(t)eiθ(τ)
其中 { a ( t ) = [ X 2 ( t ) + P 2 ( t ) ] 1 / 2 θ ( t ) = arctan ( Y ( t ) X ( t ) ) \left\{ \begin{array} { l } { a ( t ) = \left[ X ^ { 2 } ( t ) + P ^ { 2 } ( t ) \right] ^ { 1 / 2 } } \\ { \theta ( t ) = \arctan \left( \frac { Y ( t ) } { X ( t ) } \right) } \end{array} \right. {a(t)=[X2(t)+P2(t)]1/2θ(t)=arctan(X(t)Y(t))
在完成EMD后就提取了所有的IMF，对IMF进行Hilbert变换之后，就可以用下面的方式表示信号： X ( t ) = ∑ j = 1 n a j ( t ) exp ( i ∫ ω j ( t ) d t ) X ( t ) = \sum _ { j = 1 } ^ { n } a _ { j } ( t ) \exp \left( i \int \omega _ { j } ( t ) d t \right) X(t)=∑j=1naj(t)exp(i∫ωj(t)dt)
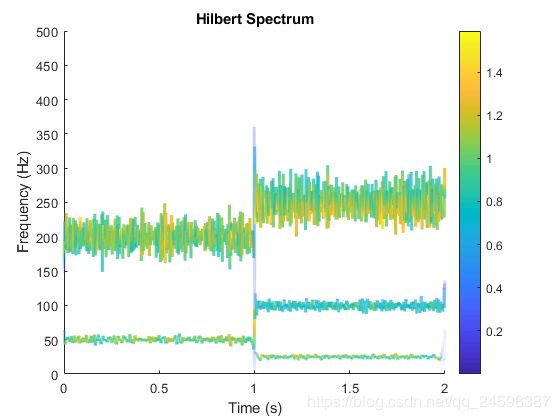
上式中忽略了余项，因为余项的能量很小，一般可以忽略不计，由Hilbert变换得到的幅值和频率都是时间的函数，如果将幅值表示在频率时间的平面上，就可以得到Hilbert谱H(w,t)，如果对H进行时间积分，就能够得到希尔伯特边际谱h（w）
h ( w ) = ∫ 0 T H ( w , t ) d t h ( w ) = \int _ { 0 } ^ { T } H ( w , t ) d t h(w)=∫0TH(w,t)dt
编辑普提供了对每个频率的总振幅的量测，表示了整个时间长度内累计的振幅，另外，作为Hilbert编辑普的附加结构，可以得到希尔伯特瞬时能量：
I E ( t ) = ∫ w H 2 ( w , t ) d w I E ( t ) = \int _ { w } H ^ { 2 } ( w , t ) d w IE(t)=∫wH2(w,t)dw
如果幅值的平方对时间积分，就可以得到Hilbe能量谱：
E S ( w ) = ∫ 0 T H 2 ( w , t ) d t E S ( w ) = \int _ { 0 } ^ { T } H ^ { 2 } ( w , t ) d t ES(w)=∫0TH2(w,t)dt
同emd函数一样，matlab也是在R2018b之后的版本中才有内置的hht函数，
- hht(imf,fs);直接根据第一步获得的IMF画出Hilbert谱
- [hs,f,t] = hht(imf,fs)
这里的返回值官方文档没有明确解释，对文献返回变量记性观察可以得到，t就是最简单的时间向量，f是将fs/2等分成100份后的一个101维的向量，而hs则是每个101*t维的矩阵，t是时间的变量的维度，同样也是IMF分量的函数
这里如果不采用hht函数， 直接画图，而根据hht变换的原理，自行进行Hiltbert变换，会发现整体，过程较为繁琐下面列出部分代码
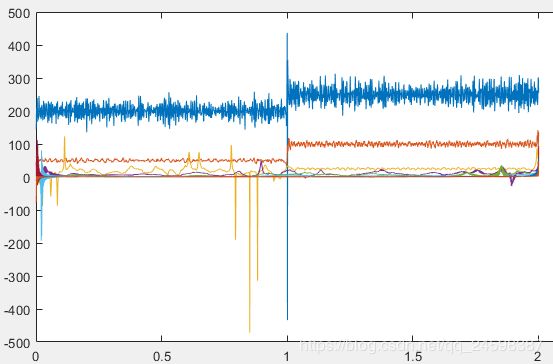
z=hilbert(imf); instfreq = fs/(2*pi)*diff(unwrap(angle(z))); figure plot(t(2:end),instfreq)
上面只是画出了每个IMF在不同时间的频率分量，并没有表示强度，可以简单地尝试使用scatter来表示强度，代码及效果如下，但依然不是非常理想，还需要后续处理，这里暂时不做过多处理tm=repmat(t,1,9); for i=1:9 scatter(t(2:end,i),instfreq(:,i),3,am(2:end,i),'filled') hold on end
分数阶Fourier变换
其他一些问题说明
是否转换为dB显示？
这里转一小段文字来说明转换为分贝的作用。
通常，振幅或功率谱以对数单位分贝(dB)的形式显示。该测量单位有助于查看宽动态范围，即可在存在较大信号分量时方便地查看小信号分量。分贝是比例单位，其计算方式如下。
其中P是测量功率，Pr是参考功率。
使用下列公式从振幅值计算分贝值。
其中A是测量振幅，Ar是参考振幅。
使用振幅或功率作为同一信号的振幅平方时，结果分贝水平是完全一致的。将分贝比乘以2，等同于将比例平方。因此，无论使用振幅或功率谱，都将得到相同的分贝水平和显示
主要参考文献
- 《基于MATLAB的机械故障诊断技术案例教程》-张玲玲，肖静 高等教育出版社2016
我们对Markdown编辑器进行了一些功能拓展与语法支持，除了标准的Markdown编辑器功能，我们增加了如下几点新功能，帮助你用它写博客： - http://blog.sina.com.cn/s/blog_15183f5750102w13a.html
- https://www.penwatch.net/cms/fft_sampling/
未完待续，持续更新中，欢迎大家指出相关问题，写到后面感觉前面突然一堆逻辑错误2333~
留言回复不及时，大佬们烦劳发一下邮箱 [email protected] 哈，谢谢大家了!