SM2算法第三篇：实现SM2秘钥交换协议的算法流程

参考文献：SM2椭圆曲线公钥密码算法-第三部分（秘钥协商协议）

一、概述

本部分规定了SM2椭圆曲线公钥密码算法的密钥交换协议，并给出了密钥交换与验证示例及相应的流程。本部分适用于商用密码 应用中的密钥交换，可满足通信双方经过两次或可选三次信息传递过程，计算获取一个由双方共同决定的共享秘密密钥（会话密钥）。同时，本部分还可为安全产品生产商提供产品和技术的标准定位以及标准化的参考，提高安全产品的可信性和互操作性。

二、术语和定义

1、密钥  key

确定密码参数运算的一个参数，它用于：

（a）加密和解密变换；

（b）同步产生共享秘钥；

（c）数字签名的生成和验证。

2、密钥交换  key exchange

在通信实体之间安全地建立一个共享秘钥的协商过程。

3、密钥协商：key agreement

多个用户之间建立一个共享秘密秘钥的过程，并且其中任何一个用户都不能预先确定该秘钥的值。

4、从A到B的密钥确认 key comfirmation from A to B

使用户B确信用户A拥有特定秘密秘钥的保证。

5、密钥派生函数  key derivation function

通过作用于共享秘密和双方都知道的其他参数，产生一个或多个共享秘密秘钥的函数。

6、杂凑函数  hash function

将一个比特串映射为一个固定长度比特串的函数，该函数满足如下性质：

（a）对于任意给定的输出，要找其对应的输入，在计算上是不可行的；

（b）对于任意给定的输入，要找到输出相同的另一个输入，在计算上是不可行的。

7、杂凑值  hash value

杂凑函数作用于一条消息时输出的比特串。

8、对称密码算法  symmetric cryptographic algrorithm

一种执行加密/解密的算法，其中加密/解密使用的秘钥容易从计算上相互求得。

9、发起方  initiator

在一个协议的操作过程中发送首轮交换信息的用户。

10、响应方  responder

在一个协议的操作过程中不是发送首轮交换信息的用户。

11、可辨别标识  disdinguishing identifier

可以无歧义辨别某一实体身份的信息。

三、符号

• A,B：使用公钥密码系统的两个用户。
• a,b：Fq中的元素，它们定义Fq上的一条椭圆曲线E。
• dA：用户A的私钥。
• dB：用户B的私钥。
• E(Fq)：Fq上椭圆曲线E的所有有理点（包括无穷远点O）组成的集合。
• Fq：包含q个元素的有限域。
• G：椭圆曲线的上一个基点，其阶为素数。
• Hash()：密码杂凑函数。
• Hv()：消息摘要长度为v比特的密码杂凑函数。

消息摘要百度百科：

• HASH函数的抗冲突性使得如果一段明文稍有变化，哪怕只更改该段落的一个字母，通过哈希算法作用后都将产生不同的值。而HASH算法的单向性使得要找到哈希值相同的两个不同的输入消息，在计算上是不可能的。所以数据的哈希值，即消息摘要，可以检验数据的完整性。
• 哈希函数的这种对不同的输入能够生成不同的值的特性使得无法找到两个具有相同哈希值的输入。因此，如果两个文档经哈希转换后成为相同的值，就可以肯定它们是同一文档。所以，当希望有效地比较两个数据块时，就可以比较它们的哈希值。例如，可以通过比较邮件发送前和发送后的哈希值来验证该邮件在传递时是否修改。

• h：余因子，h=#E(Fq)/n，其中n是Fq的阶。
• IDA，IDB：用户A和用户B的可辨别标识。
• K，KA，KB：秘钥交换协议商定的共享秘密秘钥。
• KDF()：秘钥派生函数。
• modn：模n运算。
• n：基点G的阶（n是#E(Fq）的素因子）。
• O：椭圆曲线上的一个特殊点，称为无穷远点或零点，是椭圆曲线加法群的单位元。

------------------------------------------分割线在此，不要看我（2016.04.20更新）---------------------------------------------------

• PA：用户A的公钥。
• PB：用户B的公钥。
• q：有限域Fq中元素的数目。
• rA：秘钥交换中用户A产生的临时秘钥值。
• rB：秘钥交换中用户B产生的临时秘钥值。
• x||y：x与y的拼接，其中x与y可以是比特串或字符串。
• ZA：关于用户A的可辨别标识、部分椭圆曲线系统参数和用户A公钥的杂凑值。
• ZB：关于用户B的可辨别标识、部分椭圆曲线系统参数和用户B公钥的杂凑值。
• #E(Fq)：E(Fq)上点的数目，称为椭圆曲线E(Fq)的阶。
• |k|P：椭圆曲线上点P的k倍点，k是正整数。
• x.y]：大于或等于x且小于或等于y的整数的集合。
• 顶函数：大于或等于x的最小整数。
• 底函数：小于或等于x的最小整数。
• &：两个整数按比特与运算。

四、算法参数与辅助函数

1、总则：

密钥交换协议是两个用户A和B通过交互的信息传递，用各自的私钥和对方的公钥来商定一个只有他们自己知道的秘密密钥。这个共享的秘密密钥通常用在某个对称密码算法中。该密钥交换协议能够用于密钥管理和协商。

2、椭圆曲线系统参数：

（1）有限域Fq的规模q；

（2）定义椭圆曲线E(Fq)的两个参数啊，a、b∈Fq；

（3）E(Fq)上的基点G=（xG，yG）（G≠O），其中xG、yG是Fq中的两个元素；

（4）G的阶n及其可选项（如n的余因子h等）。

3、用户密钥对

用户A的密钥对应包括其私钥dA和公钥PA=[dA]G=(xA，yA)，用户B的密钥对应包括其私钥dB和公钥PB=[dB]G=(xB，yB)。

用户密钥对的生成算法与公钥验证算法应符合第一部分第六章的规定。

4、辅助函数

（1）密码杂凑函数：如SM3；

（2）密钥派生函数：从一个共享的秘密比特串中派生出密钥数据。在密钥协商过程中，密钥派生函数作用在密钥交换所获共享的秘密比特串上，从中产生所需要的会话密钥或进一步加密所需要的秘钥数据。

密钥派生函数需要调用秘钥杂凑函数。

（3）随机数发生器：使用国密局规定的随机数发生器。

5、用户其他信息

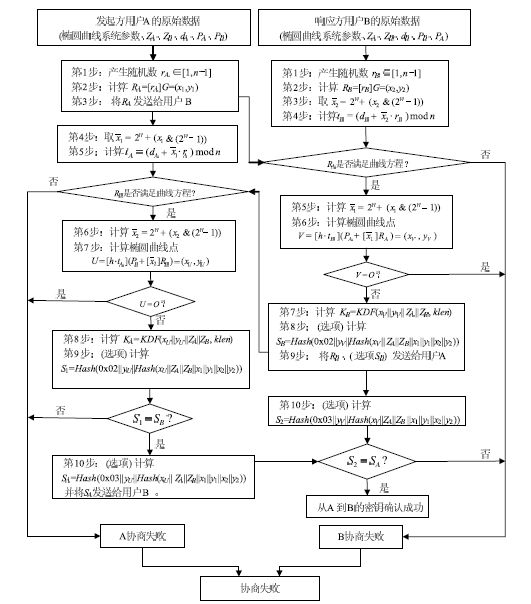
五、密钥交换协议及流程

1、密钥交换协议

设用户A和B协商获取密钥数据的长度为klen比特，用户A是发起方，用户B是响应方。用户A和B双方为了获取相同的密钥，应实现如下运算步骤：

w=[[log2(n)]/2]-1。（注：此处的[]指的是顶函数）

用户A：

A1：用随机数发生器产生随机数rA∈[1,n-1]；

A2：计算椭圆曲线点RA=[rA]G=（x1，y1）；

A3：将RA发送给用户B。

用户B：

B1：用随机数发生器产生随机数rB∈[1,n-1]；

B2：计算椭圆曲线点RB=[rB]G=（x2，y2）；

B3：从RB中取出域元素x2，按本文第一部分的4.2.7给出的方法将x2的数据类型转换为整数，计算x2`=2^w+(x2&(2^w-1))；

B4：计算tB=（dB+x2`*rB）mod n；

B5：验证RA是否满足椭圆曲线的方程，若不满足则协商失败；否则从从RB中取出域元素x1，按本文第一部分的4.2.7给出的方法将x2的数据类型转换为整数，

计算x1`=2^w+(x1&(2^w-1))；

B6：计算椭圆曲线点V=[h*tB](PA+[x1`]RA)=(xv,yv)，若V是无穷远点，则B协商失败；否则按本文第一部分4.2.5和4.2.4给出的方法将xv，yv的数据类型转换为比特串；

B7：计算KB=KDF（xv||yv||ZA||ZB，klen）；

B8：（选项）按本文第一部分4.2.5和4.2.4给出的方法将RA的坐标x1、y1和RB的坐标x2、y2的数据类型转换为比特串，计算SB==Hash.......；

B9：将RB、（选项SB）发送给用户A；

用户A：

A4：从RA中提取出域元素x1，按本文第一本分4.2.7给出的方法将x1的数据类型转换为整数，计算x1`=2^w+(x1&(2^w-1))；

A5：tA=（dA+x2`*rA）mod n；

A6：验证RB是否满足椭圆曲线的方程，若不满足则协商失败；否则从从RB中取出域元素x2，按本文第一部分的4.2.7给出的方法将x2的数据类型转换为整数，

计算x2`=2^w+(x2&(2^w-1))；

A7：计算椭圆曲线点U=[h*tA](PB+[x2`]RB)=(xu,yu)，若U是无穷远点，则A协商失败；否则按本文第一部分4.2.5和4.2.4给出的方法将xu，yu的数据类型转换为比特串；

A8：计算KA=KDF（xu||yu||ZA||ZB，klen）；

A9：（选项）计算S1，并检验S1=SB是否成立，若不成立则从B到A的秘钥确认失败；

A10：（选项）计算SA，并将SA发送给用户B。

用户B;

B10：计算S2，并检验S2=SA是否成立，若不成立则从A到B的秘钥确认失败。

（二）秘钥交换协议流程

、