C++(数据结构与算法):54---优先级队列的实现（大根堆、小根堆）

前言

• 本文代码下载：
  • CSDN下载链接：https://download.csdn.net/download/qq_41453285/12045501
  • Github下载链接(为其中的maxHeap.zip文件)：https://github.com/dongyusheng/algorithm

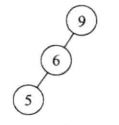
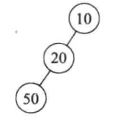
一、大根树、小根树

• 大根树：其中每个节点的值都大于或等于其子节点的值
• 小根树：其中每个节点的值都小于或等于其子节点的值

图例

二、大根堆、小根堆

• 大根堆：属于大根树的一种，但是必须是完全二叉树
• 小根堆：属于小根树的一种，但是必须是完全二叉树

图例

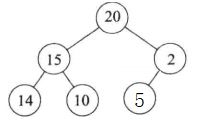
• 下面是两个大根堆，因为每个节点的值都大于其子节点的值，并且是完全二叉树

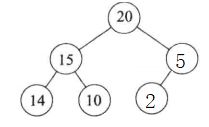
• 下面不是大根堆，因为其不是完全二叉树

• 下面是两个小根堆，因为每个节点的值都小于其子节点的值，并且是完全二叉树

• 下面不是小根堆，因为其不是完全二叉树

堆的数组表示

• 因为堆是完全二叉树，所以用一维数组表示最为有效（详情可以见文章：https://blog.csdn.net/qq_41453285/article/details/103561197）
• 如果数组的第一个位置不保存元素。且一个元素的索引为i（1<=i<=n），则有如下的规则：
  • 1.如果i=0，则该节点为根节点，无父节点。否则其父节点下标为i/2
  • 2.如果2*i>n，则该节点没有左子树；否则其左子树的下标为2*i
  • 3.如果(2*i)+1>n，则该节点没有右子树；否则其右子树的下标为2*i+1
  • 4.左子树的下标为奇数，右子树的下标为偶数
• 特征：
  • 堆是完全二叉树，具有n个元素的堆高度(height)为
  • 据上，插入和删除操作的时间为O(height)，复杂度为O()

三、大根堆的插入、删除、初始化

大根堆的插入

插入步骤如下：

• 1.将新节点插入到尾部
• 2.如果其有父节点，检查其值是否比父节点值大，如果比父节点值小，则结束本次插入操作；如果比父节点的值大，那么就将自己与父节点进行互换
• 3.如果互换之后还有父节点，那么重复步骤2直到插入操作结束

演示案例：

• 如果一个大根堆的初始化如下：

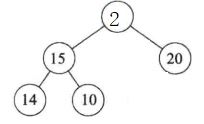
• 此时插入一个新节点5，步骤如下：
  • 1.先插入到2的节点的左子树处（如果左图所示）
  • 2.检查到新节点比2节点值大，于是就将新节点5和父节点2进行互换（如果右图所示）
  • 3.互换之后，节点5继续与父节点20比较，发现比父节点20值小，于是就结束本次插入操作，最终的大根堆如下右图所示

复杂度：

• 每一层需耗时Θ(1)，因此，实现这种插入策略的时间复杂度为

大根堆的删除

插入步骤如下：

• 1.删除根节点
• 2.将最后一个节点设置为根节点作为新根节点
• 3.如果有子节点，将新根节点与左右子树比较，如果比左右子树的值都大，则停止本次删除操作；如果比左（或右）子树的值小，那么就将自己与左（或右）子树互换；如果比左右子树都小，那么就与左右子树中较大的那个节点互换
• 4.互换之后如果还有左右子树，那么就继续执行步骤3，直到删除操作结束

演示案例：

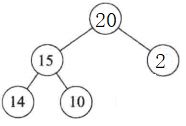
• 如果一个大根堆的初始化如下：

• 此时删除大根堆（删除根节点），步骤如下：
  • 1.删除根节点21
  • 2.将最后一个节点2设置为新根节点（如下做图所示）
  • 3.新根结点2与左右子树进行比较，发现比左子树15、右子树20都小，因此需要进行交换操作
  • 4.但是右子树20比左子树15大，因此其与右子树20交换（如下右图所示）
  • 5.交换完成之后，其没有子树了，所以就结束删除操作了（如下右图所示）

复杂度：

• 每一层需耗时Θ(1)，因此，实现这种删除策略的时间复杂度为

大根堆的初始化

规则如下：

• 1.从最后一个具有孩子的节点开始检查（这个节点位于i=[n/2]，也就是最后一个节点的父节点索引），检查其与子节点之间是否满足大根堆的条件，如果不满足就进行交换
• 2.然后继续检查i-1、i-2、等节点为根与子节点之间是否满足大根堆的条件，直至检查到以1为根的树位置
• 3.备注：如果某个根节点与子节点之间不满足大根堆的条件开始进行交换，交换之后如果这个节点还作为根节点，那么需要继续与子节点之间进行比较

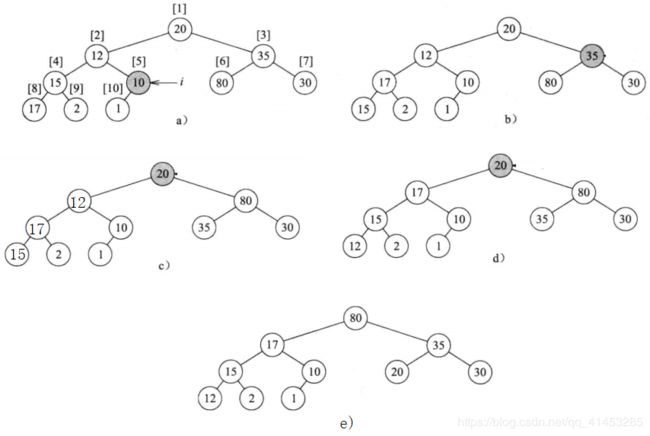
演示案例：

• 1.从最后一个具有孩子的节点开始检查（i=10/2=5），于是先检查[5]这个节点，其子节点都比其小，所以保持不变（图a所示）
• 2.接着检查i=5-1=4这个节点，检查到其值15比17小，于是进行交换，结果如图b所示
• 3.接着检查i=4-1=3这个节点，检查其值35比左子节点80值小，于是进行互换，结果如图c所示
• 4.接着检查i=3-1=2这个节点，检查其值比左子节点17小，于是与17进行互换。互换之后其还有两个子节点，于是又进行比较发现比左子节点15还小，于是就与15进行互换，结果如图d所示
• 5.接着检查i=3-1=1这个节点，检查其值比右子节点80小，于是与80进行互换。互换之后其还有两个子节点，于是又进行比较发现比左子节点35和30都小，但是左子节35点比右子节点30大，于是就与,35进行互换，结果如图e所示

四、编码实现

头文件定义

#include 
#include 
#include 
#include

using std::cout;
using std::cin;
using std::endl;
using std::string;
using std::min;
using std::copy;
using std::ostream_iterator;

异常类定义

class illegalParameterValue
{
	std::string message;
public:
	illegalParameterValue(const char *theMessage = "Illegal Parameter Value") :message(theMessage) {}
	const char *what() {
		return message.c_str();
	}
};

class queueEmpty
{
	std::string message;
public:
	queueEmpty(string theMessage ="Invalid operation on empty queue") :message(theMessage){}
	const char *what() {
		return message.c_str();
	}
};

抽象类定义

template
class maxPriorityQueue
{
public:
	virtual ~maxPriorityQueue() {}
	virtual bool empty()const = 0;//当队列为空返回true;否则返回false
	virtual int size()const = 0;//返回队列的元素个数
	virtual const T& top() = 0;//返回优先级最大的元素的引用
	virtual void pop() = 0; //删除队首元素
	virtual void push(const T& theElement) = 0;//插入元素theElement
};

全局函数定义

• 当数组空间不足时，扩充数组

template
void changeLength(T*& theElement, int oldSize, int newSize)
{
	if (newSize < 0)
		throw illegalParameterValue("newSize must be >=0");

	T *tempElement = new T[newSize];

	int min = std::min(oldSize, newSize);

	std::copy(theElement, theElement+min, tempElement);
	
	delete[] theElement;
	theElement = tempElement;
}

maxHeap类定义

template
class maxHeap :public maxPriorityQueue
{
public:
	maxHeap(int initialCapacity = 10);
	~maxHeap();

	bool empty()const override {//当队列为空返回true;否则返回false
		return this->heapSize == 0;
	}
	int size()const override{   //返回队列的元素个数
		return this->heapSize;
	}

	const T& top()override;   //返回优先级最大的元素的引用
	void pop()override;       //删除队首元素
	void push(const T& theElement)override;//插入元素theElement

	void initialize(T* theHeap, int theSize); //初始化一个大根堆

	void output(std::ostream & out)const;
private:
	T *heap;        //存放节点的数组
	int heapSize;   //队列中的元素个数
	int arrayLength;//数组长度
};

构造函数、析构函数

template
maxHeap::maxHeap(int initialCapacity = 10)
{
	if (initialCapacity <= 0)
		throw illegalParameterValue("initialCapacity must be >0");

	this->heap = new T[initialCapacity];
	this->arrayLength = initialCapacity + 1;
	this->heapSize = 0;
}

template
maxHeap::~maxHeap()
{
	if (this->heap)
		delete[] this->heap;
	this->heap = nullptr;
}

top()函数定义

• 得到队列头元素

template
const T& maxHeap::top()
{
	if (this->heapSize == 0)
		throw queueEmpty();

	return this->heap[1];
}

push()函数定义

• 向队列中（最大堆中）加入一个元素

template
void maxHeap::push(const T& theElement)
{
	//如果数组已满，扩充数组
	if (this->heapSize == this->arrayLength-1) {
		changeLength(this->heap, this->arrayLength, this->arrayLength * 2);
		this->arrayLength *= 2;
	}

	//指向最后一个节点
	int currentNode = ++this->heapSize;

	//如果当前节点比父节点值大就进行互换
	while ((currentNode > 1) && (this->heap[currentNode / 2] < theElement)) {
		this->heap[currentNode] = this->heap[currentNode / 2];
		currentNode /= 2;
	}
	
	this->heap[currentNode] = theElement;
}

pop()函数

• 从队列头取出一个元素（取出最大堆的根节点）

template
void maxHeap::pop()
{
	if (this->heapSize == 0)
		throw queueEmpty();

	//释放根节点
	this->heap[1].~T();

	//获取最后一个节点的值
	T lastElement = this->heap[this->heapSize--];
	
	//child:先与子节点比较
	int currentIndex = 1, child = 2;
	
	while (child <= this->heapSize)
	{
		//找出子节点中值大的那个节点
		if ((child < this->heapSize) && (this->heap[child] < this->heap[child + 1])) {
			child++;
		}

		//如果节点比子节点都大，结束插入操作
		if (lastElement >= this->heap[child])
			break;

		//如果比子节点小，就与子节点交换
		this->heap[currentIndex] = this->heap[child];
		//将索引移至子节点
		currentIndex = child;
		//更新子节点索引，继续与子节点比较
		child *= 2;
	}

	this->heap[currentIndex] = lastElement;
}

initialize()函数

• 删除当前堆，重新初始化一个堆

template
void maxHeap::initialize(T* theHeap, int theSize)
{
	if (this->heap)
		delete[] this->heap;
	this->heap = theHeap;
	this->arrayLength = theSize + 1;
	this->heapSize = theSize;

	//从最后一个拥有子节点的父节点开始
	for (int root = this->heapSize / 2; root >= 1; root--) {
		//获取父节点值
		T rootElement = this->heap[root];
		
		//获取左子节点的值
		int child = root * 2;

		//如果有子节点
		while (child <= this->heapSize)
		{
			//找出子节点中较大的子节点坐标
			if ((child < this->heapSize) && (this->heap[child] < this->heap[child + 1])) {
				child++;
			}

			//如果父节点比子节点都大，就结束本次循环
			if (rootElement >= this->heap[child])
				break;

			//如果父节点比子节点小，就交换值
			this->heap[child / 2] = this->heap[child];

			//交换值之后将child*2，判断是否还有子节点可以比较，如果有子节点就再执行while进行比较
			child *= 2;
		}

		this->heap[child / 2] = rootElement;
	}
}

output()函数

• 将当前队列中（最大堆）的所有元素输出到out流中

template
void maxHeap::output(std::ostream & out)const
{
	std::copy(this->heap+1, this->heap + this->heapSize + 1, ostream_iterator(std::cout, " "));
}

全局重载<<运算符

• 用来输出maxHeap对象

template
std::ostream& operator<<(std::ostream& out,maxHeap& x)
{
	x.output(out);
	return out;
}

主函数

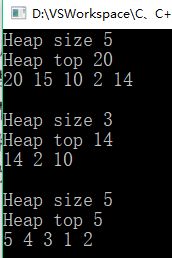
int main()
{
	maxHeap *myHeap = new maxHeap(10);

	myHeap->push(2);
	myHeap->push(10);
	myHeap->push(15);
	myHeap->push(14);
	myHeap->push(20);

	std::cout << "Heap size " << myHeap->size() << std::endl;//5
	std::cout << "Heap top " << myHeap->top() << std::endl;  //20
	std::cout << *myHeap << std::endl << std::endl; //20 15 10 2 14

	myHeap->pop();
	myHeap->pop();
	std::cout << "Heap size " << myHeap->size() << std::endl;//3
	std::cout << "Heap top " << myHeap->top() << std::endl;  //14
	std::cout << *myHeap << std::endl << std::endl;; //14 2 10

	int arr[6];
	for (int i = 1; i < 6; ++i)
		arr[i] = i;
	myHeap->initialize(arr, 5);

	std::cout << "Heap size " << myHeap->size() << std::endl;//5
	std::cout << "Heap top " << myHeap->top() << std::endl;  //5
	std::cout << *myHeap << std::endl;  //5 4 3 1 2
	return 0;
}