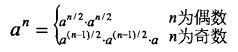《剑指offer》学习笔记

 扎实的基础知识：

1.编程语言（C++）：概念理解

                            分析代码运行结果

                            写代码定义一个类或类的成员函数（构造函数，析构函数，运算符重载）

                            《Effective C++》，《C++ primer》

---

2.数据结构（二叉树和链表）

---

（1）数组：内存连续，根据下标O(1)读写，时间效率高，可实现简单的哈希表（下标做key，数字做值），预先分配内存，总有空闲区域，空间效率低（动态数组vector）。数组名为指向数组第一个元素的指针，可通过指针访问数组元素（对数组名直接取sizeof求得的是数组大小，若用数组名当参数传递或定义指针指向数组，则sizeof结果为4个字节，因为32位系统，任意指针均为4个字节）

面试题3 二维数组的查找：从具体例子中找出其中的规律，从左下角或右上角开始，注意移动方向

时间复杂度：O(M+N)，空间复杂度O(1)

---

（2）字符串：内存连续的若干字符，以‘\0’结尾故需要一个额外字符开销，注意不要越界，需要遍历找到字符串长度，当几个指针赋值给相同的常量字符串时，实际指向相同的内存地址。

面试题4 替换空格：统计空格个数，计算newlength，length为可用长度，若newlength>length，则错误；i,j分别从newlength和length开始（‘\0’也需要判断），且若i==j则无需继续插入了；

时间复杂度：O(n)，空间复杂度O(1)

Tips:合并两个数组（字符串），若从前往后复制需要重复移动多次，可以考虑从后往前复制，能减少移动次数，从而提高效率。

---

（3）链表：动态数据结构，创建时无需知道长度，插入时为结点分配内存。然后调整指针连接，每添加一个结点分配一次内存，无闲置内存，空间效率比数组高。插入结点：

void AddToTail(ListNode ** pHead, int value)
{
	ListNode *pNew = new ListNode(-1);
	pNew -> val = value;
	pNew -> next = NULL;
	if (*pHead == NULL)
		pHead = pNew;
	else
	{
		ListNode *pNode = *pHead;
		while (pNode -> next != NULL)
			pNode = pNode -> next;
		pNode -> next = pNew;
	}
}

注意：pHead为指向指针的指针，当往空链表中插入时，插入的结点即为头指针，由于会改变头指针，故设为指向指针的指针，否则出了这个函数仍为空指针

面试题5 从尾到头打印链表：利用栈实现逆序，基本操作push，pop，或利用vector来reverse；

时间复杂度：O(n)，空间复杂度O(n)

Tips：递归本身就是一个栈结构，用栈来实现的函数可以考虑用递归实现，但递归可能导致调用栈溢出，故显式用栈基于循环实现的代码鲁棒性更高一些。

---

（4）树：除根结点外每个结点只有一个父结点；除叶结点外所有结点有一个或多个子结点，父结点与子结点间用指针链接。常见的为二叉树，每个结点最多两个子结点，最重要的操作为遍历（前序遍历，中序遍历，后序遍历各有递归和循环两种实现方法需了如指掌），另外还有层次遍历。参见：https://blog.csdn.net/qy724728631/article/details/81835654

二叉搜索树，左子树结点总是小于等于根结点而右子结点总是大于等于根结点，可在O(logn)的时间内找到一个结点。

堆分为最大堆和最小堆指的是根结点最大或最小，快速找到最值可用堆解决。

红黑树，根为红和黑两种，通过规则确保从根结点到叶结点的最长路径不超过最短路径的二倍，set，multiset，map，multimap等数据结构均基于红黑树实现。

面试题6 重建二叉树：根据先序遍历序列第一个数字确定根节点，在中序遍历序列中找到根节点，划分出左子树和右子树的前序遍历和中序遍历序列，递归求解, 停止条件：pl > pr；

时间复杂度：每次在中序遍历中找根节点的位置需要O(n)的查找时间，推导复杂度： 
　　　　T(n) = 2 * T(n / 2) + O(1) + O(n)    T(n) = O(nlog(n)) 

空间复杂度：递归求解，因为每个节点都会被递归到，所以空间复杂度为O(n)。

---

（5）栈和队列：栈先入后出，最后push的最先pop，栈是一个不考虑排序的数据结构，需要O(n)才能找到最大值或最小值；队列先入先出，注意二者的相互联系。

面试题7 用两个栈实现队列：用第一个栈输入，输出则输出第二个栈，若其为空则将第一个栈输出至第二个栈再输出；

时间复杂度：O(n)   空间复杂度：O(n)

---

3.算法

（1）查找

查找：顺序查找，二分查找，哈希表查找，二叉排序树查找

Tips: 在排序的数组（或部分排序的数组）中查找---二分查找；

int binarySerach(int[] array, int key) 
{
    int left = 0，right = array.length - 1;
    while (left <= right) 
    {
        int mid = left + (right - left) / 2;
        if (array[mid] == key) 
            return mid;
        else if (array[mid] < key)
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;
}

哈希表查找：O(1)的时间效率，但需要额外的空间来实现哈希表

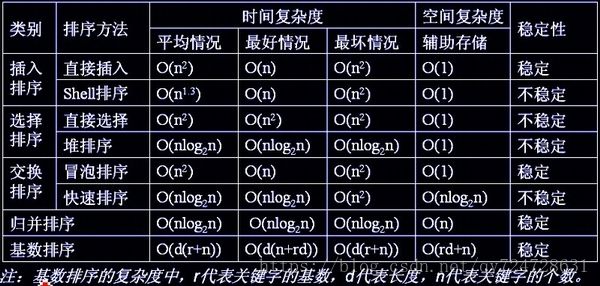
（2）排序

比较各种排序算法空间消耗，平均和最坏时间复杂度

快排的代码：

int Partition(int data[], int length, int start, int end)
{
     if (data == NULL || length <= 0 || start< 0 || end >= length)
            throw new exception(“ InvalidParameters”);
     int index = RandomInRange(start, end);
     Swap(&data[index], &data[end]);
     int small = start – 1;
     for(index = start; index < end; ++ index)
     {
         if(data[index]< data[end])
         {
               ++ small;
               if (small != index)
                  Swap (&data[index],&data[small])
         }
     }
    ++ small;
    Swap(&data[small],&data[end]);
    return small;
}
      
Void QuickSort(int data[], int length, int start, int end)
{
     if (start == end)
           return;
     int index = Partition(data, length, start,end);
     if (index > start)
           QuickSort (data, length, start, index – 1);
     if (index < end)
           QuickSort (data, length, index + 1, end);
}

Tips: 当数据位于一定数据范围内可以采用计数排序，对待排序序列中的每种元素的个数进行计数，然后获得每个元素在排序后的位置的信息的排序算法。时间复杂度为O(n)，稳定，空间复杂度O(k), k为数字取值种类。

面试题8 旋转数组的最小数字：二分法，一指针start指向头，一指针end指向尾，若两指针相邻则返回end；若mid大于等于第一个指针，则start = mid + 1；否则若mid小于等于第二个指针，则end = mid - 1；注意考虑本身即为排序数组（故mid初始值为start，循环条件为a[start] >= a[end]）和有重复元素的情况(a[start] == a[end] == a[mid] 则start++)。

时间复杂度：O(logn)   空间复杂度：O(1)

---

（3）递归和循环

若无特殊要求，优先使用递归算法。

递归简洁，但时间和空间消耗大（调用栈溢出），且很多计算是重复的，性能不好

面试题9 斐波那契数列：f(n) = f(n-1)+ f(n-2)  ： n<=1 return n; 通过更新记录first和second，取代递归。

时间复杂度：O(n)   空间复杂度：O(1)

题目二 跳台阶：同上

题目三 变态跳台阶：f(n) = f(n - 1) + ... + f(1) --->  f(n) = 2f(n-1)  ----> f(n) = 2^(n-1)

题目四 矩形覆盖：f(n) = f(n-1)+ f(n-2)  ： n<=1 return n;

---

（4）位运算：与，或，异或，左移（右侧补零），右移（有符号数左移补符号位，无符号数则补零）。

***  负整数右移与直接除以2是不等价的，因为右移后前面会补位1

***  判断整数某位是不是1：将整数与1做位与运算，

      对于正整数，从右侧逐次与1做位与运算后依次右移，判断各位是否为1

      对于负整数，可以采用将1逐次左移后与负数做位与运算，判断各位是否为1

***  一个整数减一后再与原来做位与运算，相当于把二进制最右边一个1变为0

***  位移运算要比乘除运算效率高得多,此外用&1来判断奇数比用%效率高

面试题10 二进制中1的个数：巧用n & (n - 1)

时间复杂度：O(logn)   空间复杂度：O(1)

题目二：判断整数是不是2的整数次方：n & (n - 1) == 0？

题目三：输入两个整数m和n，计算需要改变m二进制中多少位才能得到n：a = m ^ n; a = a & (a - 1);

---

高质量的代码

完整性，完成基本功能，边界条件，内存覆盖，特殊输入（空指针，0，空字符串），错误处理（输入不合法）

面试题11 数值的整数次方：注意负指数及零指数的特殊情况以及求幂次方的简化计算

                                            

 

时间复杂度：O(logn)   空间复杂度：O(1)

Tips：不能直接用等号判断两个小数相等，用两个小数的差的绝对值很小表示，比如小于10^(-7)

---

面试题12 打印1到最大的n位数 ：大数问题要用字符串或数组表示

Tips: 若关于n位整数并且没有限定n的取值范围，或者输入任意大小的整数，则可能需要考虑大数问题，字符串是一个简单，有效的表示大数的方法。

---

面试题13 在O(1)时间删除链表结点：对于n-1个非尾结点，在O（1）把下一个结点的内存复制到要删除的结点，并删除下一个结点；对于尾结点，由于需要顺序查找前一个结点，时间复杂度为O(n),对于只有一个结点的情况，删除后还要把头结点置为NULL。平均后为[（n-1）*O(1) + 1 * O（n）]/n = O(1)

时间复杂度：O(1)   空间复杂度：O(1)

---

面试题14 调整数组顺序使奇数位于偶数前面：

若不需保持相对位置不变：前后两个指针，对应交换，类似快排，时间复杂度为O(n)，空间复杂度为O(1)

若需要保持相对位置不变：类似插入排序，若插入为奇数，则尝试向前移动，时间复杂度为O(n^2)，空间复杂度为O(1)

---

面试题15 链表中倒数第k个结点：定义两个指针，第一个先走k-1步，第二个再开始，直至第一个指针到最后一个结点

注意pListHead和k值的判断，若k-1步未结束就走到最后一个结点，即k大于全长，返回NULL

题目二：求链表的中间结点，快慢指针，快指针走到末尾时，慢指针指向中间。

题目三：判断链表中有环，快慢指针，若相遇则为环，若均走到结尾（NULL）则无环

Tips：当一个指针遍历不能解决时，尝试使用两个指针遍历，一快一慢或让一个指针在链表上先走若干步。

时间复杂度：O(n)   空间复杂度：O(1)

---

 

 

***面试题16 反转链表： 注意对输入只有一个结点和输入为空的判断，定义三个指针，分别指向当前遍历到的结点，它的前一个结点及后一个结点，注意防止链表断开。

时间复杂度：O(n)   空间复杂度：O(1)

---

***面试题17 合并两个排序的链表： 注意对空链表的判断，合并需要修改头结点，故设立新的虚拟头结点。

时间复杂度：O(n)   空间复杂度：O(1)

---

面试题18 树的子结构： 第一步在树中找到与根节点值一样的结点，实际上就是树的遍历，然后递归地在左子树和右子树中寻找。（先序遍历将输出变成对结构的判断）

---

分析思路清晰

画图形象化（二叉树，链表等）

面试题19 二叉树的镜像： 先序遍历将输出变成交换非叶结点的左右子节点

***面试题20 顺时针打印矩阵： 将矩阵分成若干个圈，注意左上角行标列标总相同，且cols > start * 2并且rows > start * 2，

每次循环共分四步：1是必须的，2前提是有两行，3前提是有两行两列，4是有三行两列，不然会重复输出

---

举例具体化

面试题21 包含min函数的栈： 使用另一个栈存储当前的最小值，入栈时当前值小于等于最小栈的栈顶时入栈，出栈时若等于最小栈的栈顶元素，则将最小栈栈顶也出栈。

面试题22 栈的压入、弹出序列： 使用另一个栈做试验，若栈顶元素不是该出栈的元素，则持续按照入栈顺序入栈；若所有该出栈均出栈则为true，若直至最后仍找不到该出栈元素则为false

面试题23 从上往下打印二叉树： 二叉树的层次遍历

Tips：从上到下按层遍历二叉树本质上就是广度优先遍历二叉树

面试题24 二叉搜索树的后序遍历序列：前半部分小于最后一个值，后半部分大于最后一个值，若不满足直接返回false，满足则递归判断前后子序列是否为二叉搜索序列。

Tips：处理二叉树的遍历序列，先找到根节点，再基于根节点分为左右两个子序列，递归处理。

面试题25 二叉树中和为某一值的路径：定义全局变量vector > res存多次结果， vector path存一次结果;

深度优先遍历（dfs），注意停止条件为叶子结点且值与要求相等，不可等到NULL，会重复记录。

 

---

分解简单化（递归—分治法和动态规划）

面试26 复杂链表的复制：若直接复制，random的位置每次都需要重头查找，复杂度为O(n^2)，分三步：生成复制结点分别插在原结点后面连起来；为复制结点的random赋值为原结点的random的next（注意random可能为NULL）；取出长链中的偶数结点，注意不可更改原链表，故奇数结点的指针也需要修改。

时间复杂度：O(n)   空间复杂度：O(1)

***面试27 二叉搜索树与双向链表：中序遍历（记录链表中最后一个结点的地址（因为需要修改最后一个地址）），先递归的处理左子树，处理当前节点（当前节点左指针指向last，last右指针指向当前节点），递归右子树，一直寻找左孩子，直至左孩子为空则为链表头结点。

时间复杂度：O(n)   空间复杂度：O(1)

***面试28 字符串的排列：dfs 每次选择一个字符就将其从str中去掉后继续搜索，不选择就将其补回来继续搜索

题目二：字符串的所有组合：dfs同时传入一个start，不选则继续循环，选择入path后，更新start继续dfs

Tips：若要求按照一定要求摆放若干个数字，可以先求出数字的所有排列，然后一一判断是否满足要求。

---

优化时间和空间效率

编程习惯：比如用引用或指针传递代替值传递

算法实现：用动态规划代替递归

数据结构：巧用排序，哈希表等

***面试29 数组中出现次数超过一半的数字：

（1）若允许改变数组，则使用partition

（2）若不允许改变数组，则采用统计次数的方法，相同则累加，不同则统计新的数字，最后判断一下最后一个被统计的数字是否出现超过半数以上。

时间复杂度：O(n)   空间复杂度：O(1)

***面试30 最小的k个数：

（1）若允许改变数组，则使用partition，时间复杂度：O(n)   空间复杂度：O(1)

（2）若不允许改变数组，则采用其他结构构建数据容器，如二叉树构建最大堆，先组成大小为k的容器，然后逐个元素插入调整，时间复杂度：O(n*logk)   空间复杂度：O(1)，适合n很大而k较小的海量数据处理问题。

***面试31 连续子数组的最大和：用temp存前i-1个值得和，若temp<0 直接舍弃，从当前i加起，否则temp+当前值，若temp大于sum，更新sum

面试32 从1到n整数中1出现的次数：

将n的各个位分为两类：个位与其它位。 对个位来说：

• 若个位大于0，1出现的次数为round*1+1
• 若个位等于0，1出现的次数为round*1

对其它位来说，记每一位的权值为base，位值为weight，该位之前的数是former

• 若weight为0，则1出现次数为round*base
• 若weight为1，则1出现次数为round*base+former+1
• 若weight大于1，则1出现次数为rount*base+base

时间复杂度：O(logn)   空间复杂度：O(1)

面试33 把数组排成最小的数： to_string()将int转为string更好比较（解决大数问题），按照直接选择排序进行比较ab和ba哪个大，按最终排序后输入到str

时间复杂度：O(n^2 )   空间复杂度：O(1)

---

空间换时间：分配少量辅助空间保存计算中间结果以提高时间效率

面试34 丑数：生成ugly[index]，记录从小到大排序的丑数，ugly[i] = min(min(ugly[num_2]*2,ugly[num_3]*3),ugly[num_5]*5); 竞争排序，竞争上后更新num_i，直至num_i ++ ，直至ugly[num_i]能够大于排序后的最后一个丑数

时间复杂度：O(n )   空间复杂度：O(n)

面试题35 第一个只出现一次的字符：map（char,int）

时间复杂度：O(n )   空间复杂度：O(n)

面试题36 数组中的逆序对： 先将数组分割成子数组，先统计子数组内部的逆序对数目，然后再统计两个相邻子数组之间的逆序对数目，统计的同时，对数组排序，防止重复计算，实质上为归并排序。

时间复杂度：O(nlogn )   空间复杂度：O(n)

面试题37 两个链表的第一个公共结点：注意若有公共结点一定呈Y字型

       while(p != q)
        {
            p = p != NULL ? p -> next : pHead2;
            q = q != NULL ? q -> next : pHead1;
        }

时间复杂度：O(m+n )   空间复杂度：O(1)

---

学习沟通能力

观点明确，逻辑清晰，团队合作意识

最近看的书和学到的技术，对新概念的理解能力

知识迁移能力（举一反三）

面试题38 数字在排序数组中出现的次数：利用二分法分别查找第一个k的位置和最后一个k的位置，然后计算次数

时间复杂度：O(logn )   空间复杂度：O(1)

面试题39 二叉树的深度：左右子树中深度较大的加1

题2 平衡二叉树：左右子树中深度较大的加1

 

抽象建模能力，发散思维能力