数据结构（C/C++）课程阶段总结（八）

写在前面

课程采用教材《数据结构(C语言版)》严蔚敏，吴伟民，清华大学出版社。
本系列博文用于自我学习总结和期末复习使用，同时也希望能够帮助到有需要的同学。如果有知识性的错误，麻烦评论指出。
本次实验实现稀疏矩阵的转置和快速转置。

稀疏矩阵抽象数据类型定义

本次实验中抽象数据类型定义如下：
ADT SparseMatrix {
数据对象：D={aij|i=1,2,…,m;j=1,2,…,n; aij∈ElemSet，m和n分别称为矩阵的行数和列数}
数据关系：R={Row,Col}
Row={|1≤i≤m,1≤j≤n-1}
Col={|1≤i≤m-1,1≤j≤n}
基本操作：
TransposeSMatrix(M, &T)
初始条件：采用三元组表存储表示，T为M的转置矩阵。
操作结果：求M的转置矩阵，并用T传出。
FastTransposeSMatrix(M, &T)
初始条件：采用三元组表存储表示，T为M的转置矩阵。
操作结果：求M的转置矩阵，并用T传出。
}ADT SparseMatrix

基本操作的实现方法

在总结（七）中，实现了稀疏矩阵的一些基本操作，将其封装成头文件TSMatrixH.h。具体的封装办法是，保留三元组结构体，构造TSMatrix类，属性与原来的结构体一样，成员函数直接移植过来即可。与之前操作相同的是，所有的属性和操作均为公共成员，便于访问。

转置

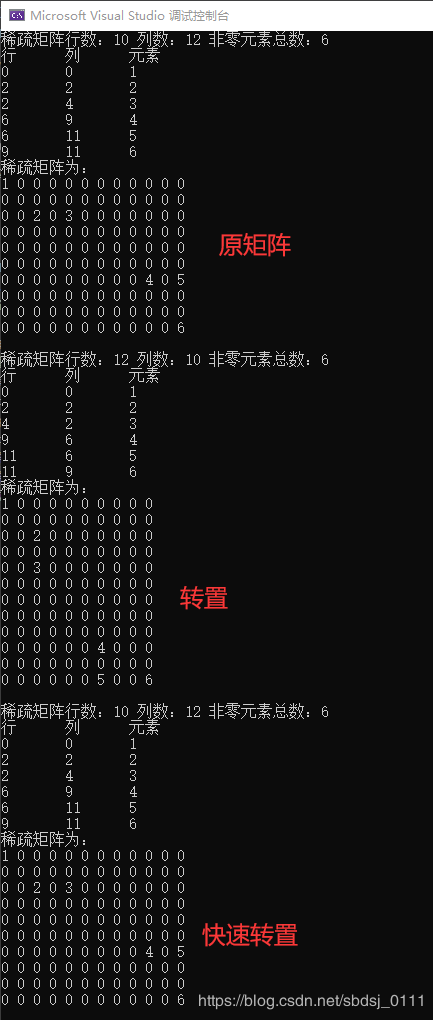
目标：获取稀疏矩阵M的转置矩阵T。
具体过程：
先将稀疏矩阵的行列数交换，再遍历原矩阵每一列，只要原矩阵的三元表在当前列上有元素，也即当前列上有非零元素，就将该位置的三元组交换行列，元素赋值，放入新的三元表中，新三元表的插入位置后移。

快速转置

目标：快速获取稀疏矩阵M的转置矩阵T。
具体过程：
快速转置的思想是，预先获取每个三元组在新三元表中的位置，再对号入座。这样就需要附设num和cpot两个向量。num[col]表示矩阵M中第col列中非零元素的个数，cpot[col]指示M中第col列的第一个非零元素在新三元表中的恰当位置。
具体的算法是，先将矩阵M的行数，列数，以及非零元个数传给矩阵T，然后初始化数组num全为0，并求出M中每一列含非零元的个数，放入num对应位置。具体的语句是，当原三元表M中有多个三元组的列数相同时，M.data[t].j是相同的，循环结束后，对应列数的非零元素个数即可获得。
获取每一列中非零元素个数后，再用关系式cpot[col]=cpot[col-1]+num[col-1]计算出每一列中第一个非零元素的位置，cpot的初始位置为1，即第一个非零元素在新三元表中的位置。
最后遍历三元表M。取M当前位置三元组的列，然后从cpot中获取当前列第一个未插入新三元表T的非零元素在新三元表T中的位置。在T的合适位置交换行列和元素赋值后，当前列中非零元素的插入位置要加1，等到下一次遇到相同列时，插入位置即为此插入位置的下一个。

具体实现

TSMatrixH.h头文件放在文末。

//1、用到的头文件、命名空间和函数执行结果状态代码
#include 
#include "TSMatrixH.h"
using namespace std;

//2、基本操作侧函数原型说明及实现
//-----基本操作的函数原型说明-----
Status TransposeSMatrix(TSMatrix M, TSMatrix& T);
// 初始条件：采用三元组表存储表示，T为M的转置矩阵。
// 操作结果：求M的转置矩阵，并用T传出。
Status FastTransposeSMatrix(TSMatrix M, TSMatrix& T);
// 初始条件：采用三元组表存储表示，T为M的转置矩阵。
// 操作结果：求M的转置矩阵，并用T传出。

//-----基本操作的算法描述-----
Status TransposeSMatrix(TSMatrix M, TSMatrix& T) {
	// 求M的转置矩阵，并用T传出。
	T.col = M.row; T.row = M.col; T.num = M.num;// 交换行列数
	if (!T.num)return ERROR;// 稀疏矩阵为0矩阵
	int locT = 0;// 转置矩阵三元组表的遍历位置
	for (int col = 0; col < M.col; col++)// 以列主序遍历原稀疏矩阵
		for (int locM = 0; locM < T.num; locM++)// 遍历原三元组表
			if (M.data[locM].j == col)// 如果原三元组的列等于当前遍历的列
			{// 则用新三元组存储当前三元组
				T.data[locT].i = M.data[locM].j; T.data[locT].j = M.data[locM].i;
				T.data[locT].e = M.data[locM].e; locT++;// 交换行列，元素赋值，新三元组表后移
			}
	return OK;
}// TransposeSMatrix

Status FastTransposeSMatrix(TSMatrix M, TSMatrix& T) {
	// 求M的转置矩阵，并用T传出。
	T.col = M.row; T.row = M.col; T.num = M.num;// 交换行列数
	if (!T.num)return ERROR;// 稀疏矩阵为0矩阵
	int* num = new int[M.col], * cpot = new int[M.col];// 定义两个向量num，cpot
	for (int col = 0; col < M.col; col++)*(num + col) = 0;// 初始化num为0
	for (int t = 0; t < M.num; t++)num[M.data[t].j]++;// 求原矩阵每一列中非零元素个数
	*(cpot) = 1;// M第一列如果有非零元素，则为新三元组表T的第一个三元组，否则自然后移列数
	for (int col = 1; col < M.col; col++)// 从M矩阵的第2列开始遍历
		*(cpot + col) = *(cpot + col - 1) + *(num + col - 1);// 求取M第1列外，M每一列第一个非零元素的位置
	for (int locM = 0; locM < M.num; locM++)// 遍历M
	{
		int col = M.data[locM].j, locT = *(cpot + col) - 1;// 确定M三元组表当前位置非零元素在T中的位置
		T.data[locT].i = M.data[locM].j; T.data[locT].j = M.data[locM].i; T.data[locT].e = M.data[locM].e;// 交换行列，获取元素值
		 cpot[col]++;// 如果M一列中有多个非零元素，则再次遇到同一列的非零元素时，插在上一个非零元素之后
	}
	return OK;
}// FastTransposeSMatrix

int main()
{
	ElemType* S[10], e;
	for (int i = 0; i < 10; i++)// 创建10*12的矩阵，由4个一维数组组成
		S[i] = new ElemType[12];// 申请空间
	for (int i = 0; i < 10; i++)
		for (int j = 0; j < 12; j++)
			*(S[i] + j) = 0;// 全部赋0
	S[0][0] = 1;// 在(0,0)位置赋1
	S[2][2] = 2;// 在(2,4)位置赋2
	S[2][4] = 3;// 在(2,2)位置赋3
	S[6][9] = 4;// 在(6,9)位置赋4
	S[6][11] = 5;// 在(9,11)位置赋5
	S[9][11] = 6;// 在(6,11)位置赋6
	TSMatrix M, T, N;// 创建三元组顺序表
	M.CreateTSMatrix(M, S, 10, 12);// 用三元组表存储稀疏矩阵
	M.DispTSMat(M);// 输出三元组表
	M.DispSMat(M);// 输出稀疏矩阵

	TransposeSMatrix(M, T);
	T.DispTSMat(T);// 输出三元组表
	T.DispSMat(T);// 输出稀疏矩阵

	FastTransposeSMatrix(T, N);
	N.DispTSMat(N);// 输出三元组表
	N.DispSMat(N);// 输出稀疏矩阵
	return 0;
}

运行结果

总结

对比两种转置方法，经典转置方法的时间复杂度为O(row×col)，虽然节省了存储空间，但时间复杂度提高了，仅适用于num≪row×col的情况；快速转置方法的时间复杂度为O(col+num)，在M的非零元素个数num和row×col同量级时，和经典转置方法的时间复杂度相同，但需要多用两个辅助向量，多占用一些存储空间。
关于两个辅助向量的实现，采用的是指针数组，目的同上一实验一样，尽量减少预定义常数的使用，使程序更加灵活，通用。当然这也带来了一些问题，比如容易造成内存泄漏，数组访问越界等，编程时需要多加注意。
三元组顺序表又称有序的双下标法，它的特点是，非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算。然而，若需按行号存取某一行的非零元，则需要从头开始查找。这就引出了其他的表示方式。

TSMatrixH.h

//#pragma once
#ifndef TSMATRIXH_H
#define TSMATRIXH_H
//1、用到的头文件、命名空间和函数执行结果状态代码
#include 
using namespace std;
//函数结果状态代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型，其值是函数结果状况代码
typedef int Status;
typedef int ElemType;//将ElemType定义为int类型
//2、采用的存储结构
//-----稀疏矩阵的三元组顺序表存储表示-----
#define MAXSIZE 125 // 假设非零元个数的最大值为125
struct Triple {
	int  i, j;// 该非零元素的行下标和列下标
	ElemType e;// 该非零元素的值
};
class TSMatrix {
public:
	Triple data[MAXSIZE + 1];// 非零元三元组表，data[0]未用
	int row, col, num;// 矩阵的行数、列数和非零元个数
public:
	//-----基本操作的算法描述-----
	Status CreateTSMatrix(TSMatrix& TSMat, ElemType* S[], int row, int col) {
		// 用三元组表TSMat存储S，并返回OK。
		TSMat.num = 0; TSMat.row = row; TSMat.col = col;// 非零元素数置零，获取稀疏矩阵的行列数
		for (int i = 0; i < row; i++)// 遍历稀疏矩阵行
			for (int j = 0; j < col; j++)// 遍历稀疏矩阵列
				if (*(S[i] + j))// 如果当前元素非零
				{// 取出当前元素的信息
					TSMat.data[TSMat.num].e = *(S[i] + j);// 元素值放入三元组
					TSMat.data[TSMat.num].i = i;// 元素行位置
					TSMat.data[TSMat.num].j = j;// 元素列位置
					TSMat.num++;// 非零元素个数加1
				}
		return OK;
	}// CreateTSMatrix
	Status ChangeValue(TSMatrix& TSMat, ElemType e, int i, int j) {
		// 修改稀疏矩阵的i，j位置的元素为e。
		int loc = 0;// 三元组顺序表位置置零
		if (i >= TSMat.row || j >= TSMat.col)return ERROR;// 判断修改位置的合法性
		while (TSMat.data[loc].i < i && loc < TSMat.num)loc++;// 遍历三元组中的行，直到修改位置的行数或表尾
		while (TSMat.data[loc].j < j && TSMat.data[loc].i == i && loc < TSMat.num)loc++;// 遍历三元组中的列，直到修改位置的列数或表尾
		if (TSMat.data[loc].i == i && TSMat.data[loc].j == j && e)// 如果修改位置元素且e不为0
			TSMat.data[loc].e = e;// 则修改此位置元素为e
		else if (e)// 如果修改位置元素为0但e不为0
		{// 则在三元组表的loc位置插入e
			for (int k = TSMat.num - 1; k >= loc; k--)// loc位置之后的元素整体后移一位
				TSMat.data[k + 1] = TSMat.data[k];// 结构体整体赋值
			TSMat.data[loc].i = i; TSMat.data[loc].j = j; TSMat.data[loc].e = e;// 插入e，及e在稀疏矩阵中的位置
			TSMat.num++;// 非零元素个数加1
		}
		else if (TSMat.data[loc].i == i && TSMat.data[loc].j == j)// 如果修改位置元素不为0但e为零
		{// 则删除三元组表的loc位置元素
			for (int k = loc; k < TSMat.num; k++)// loc位置之后的元素整体前移一位
				TSMat.data[k] = TSMat.data[k + 1];// 结构体整体赋值
			TSMat.num--;// 非零元素个数减1
		}
		return OK;
	}// ChangeValue
	Status GetValue(TSMatrix& TSMat, ElemType& e, int i, int j) {
		// 获取稀疏矩阵的i，j位置的元素并用e传出。
		int loc = 0;// 三元组表位置初始为0
		if (i >= TSMat.row || j >= TSMat.col)return ERROR;// 判断查找位置的合法性
		while (loc < TSMat.num && TSMat.data[loc].i < i)loc++;// 遍历三元组中的行，直到查找位置的行数或表尾
		while (TSMat.data[loc].i == i && loc < TSMat.num && TSMat.data[loc].j < j)loc++;// 遍历三元组中的列，直到查找位置的列数或表尾
		if (TSMat.data[loc].i == i && TSMat.data[loc].j == j)// 如果查找位置元素不为零
			e = TSMat.data[loc].e;// 则传出查找位置元素的值
		else// 如果查找位置元素为0
			e = 0;// 则传出0
		return OK;
	}// GetValue
	void DispTSMat(TSMatrix TSMat) {
		// 输出三元组表。
		if (TSMat.num <= 0)return;
		cout << "稀疏矩阵行数：" << TSMat.row << " 列数：" << TSMat.col << " 非零元素总数：" << TSMat.num << "\n";
		cout << "行\t" << "列\t" << "元素\n";
		for (int i = 0; i < TSMat.num; i++)// 按顺序遍历三元组表
			cout << TSMat.data[i].i << "\t" << TSMat.data[i].j << "\t" << TSMat.data[i].e << "\n";
	}// DispTSMat

	void DispSMat(TSMatrix TSMat) {
		// 输出稀疏矩阵。
		if (TSMat.num <= 0)return;
		int loc = 0;
		cout << "稀疏矩阵为：\n";
		for (int i = 0; i < TSMat.row; i++)// 遍历行
		{
			for (int j = 0; j < TSMat.col; j++)// 遍历列
			{
				if (TSMat.data[loc].i == i && TSMat.data[loc].j == j)// 如果当前位置元素不为0
				{// 则输出当前位置元素
					cout << TSMat.data[loc].e << " ";
					loc++;
				}// 否则输出0
				else cout << 0 << " ";
			}cout << endl;// 一行遍历结束
		}cout << endl;
	}// DispSMat
};
#endif