MATLAB编程（4）——MATLAB绘制二维高斯函数的三维图

本篇博文记录使用MATLAB绘制二维高斯函数的三维图。

用到的MATLAB函数——mesh()（绘制三维线框图）和surf()（绘制三维表面图）。

MATLAB命令窗口输入>> doc 函数名，可以查看相关函数的帮助文档。

---

一维高斯函数：

        （μ为均值，σ为标准差）

二维高斯函数：

        （这里，均值均为零，标准差均为σ）

---

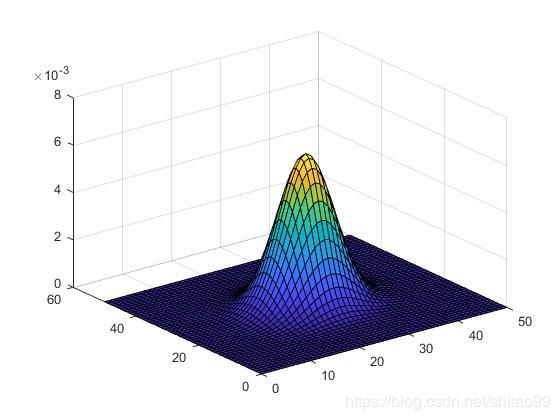
下面给出代码（两种实现结果），绘制一个均值为25，标准差为5的二维高斯函数的三维图：

代码实现一：

% 先限定三维图中的x,y轴坐标范围
X = 0 : 1 : 50;
Y = 0 : 1 : 50;

% 标准差
sigma = 5;


Z = zeros( 51, 51 );
for row = 1 : 1 : 51
    for col = 1 : 1 : 51
        Z( row, col ) = ( X(row) - 25 ).^2 + ( Y(col) - 25 ).^2; % 均值(25, 25)
    end
end
Z = -Z / ( 2 * sigma^2 );

Z = exp(Z) / ( 2 * pi * sigma^2 );

% 显示高斯函数的三维曲面
figure, surf(X, Y, Z);

结果图：

代码实现二：（更推荐）

% 先限定三维图中的 x,y 轴坐标范围
X = 0 : 1 : 50;
Y = 0 : 1 : 50;

% 标准差
sigma = 5;

[ XX, YY ] = meshgrid( X, Y );
Z = ( XX - 25 ).^2 + ( YY - 25 ).^2;

Z = -Z / ( 2 * sigma^2 );
Z = exp(Z) / ( 2 * pi * sigma^2 );

% 显示高斯函数的三维图
figure, mesh(X, Y, Z); % 线框图

结果图：

以上两种代码实现中，差别在于Z的计算。代码实现一中，使用了双层for循环，时间会比代码二长。而代码实现二中，利用向量化运算取代for循环（即向量化循环），代码的效率会更高，更值得推荐。（这也是MATLAB编程上的一个技巧）。

并且，使用meshgrid，不会受到坐标（索引）为零的影响。例如：

% 先限定三维图中的 x,y 轴坐标范围
X = -25 : 1 : 25;
Y = -25 : 1 : 25;

% 标准差
sigma = 5;

[ XX, YY ] = meshgrid( X, Y );
Z = ( XX ).^2 + ( YY ).^2; % 均值为（0,0）

Z = -Z / ( 2 * sigma^2 );
Z = exp(Z) / ( 2 * pi * sigma^2 );

% 显示高斯函数的三维图
figure, mesh(X, Y, Z); % 线框图

结果图：

以上三维图中，MATLAB默认绘制彩色图。

colormap( [0 0 0] ); % 或者 colormap( gray ) —— 可以将以上彩色三维图转换为灰色。

另外，还可控制三维图中的网格显示和坐标轴显示。

grid off; % 关闭网格 （grid on —— 开启网格）

axis off; % 关闭坐标轴显示 （axis on —— 开启坐标轴显示）

 

以上内容可用于二维滤波器的三维可视化。相关内容在书籍《数字图像处理（MATLAB版）》“4.5 在频域中直接生成滤波器”章节也有讲述。

 

---

下面的这段文字是对上述向量化循环的扩展，文字引自《数字图像处理（MATLAB版）》/（美）冈萨雷斯等著；阮秋琦等译.北京：电子工业出版社，2005,9.

MATLAB使用函数meshgrid来实现二维函数的评估，该函数的语法为：

[ C, R ] = meshgrid( c, r );

该函数将由行向量c和r指定的域变换为数组C和R，这两个数组能用来评估有两个变量的函数和三维表面图（注意，在meshgrid的输入输出中，列总是首先列出）。

输出数组C的行是向量c的副本，输出数组R的列是向量r的副本。

例如，假设我们想形成一个二维函数，该函数的元素是坐标变量x和y的值的平方和，其中，x=0,1,2  y=0,1。向量r由坐标的行分量构成：r=[0,1,2]；类似地，向量c由坐标的列分量构成：c=[0,1]，这里r和c均为行向量。

将这两个向量代入meshgrid，可得如下数组：

>>[ C, R ] = meshgrid( c, r )

C = 

       0     1

       0     1

       0     1

R =

       0      0

       1      1

       2      2

>>h = R .^2 +C .^2

h =

       0      1

       1      2

       4      5

h的维度为length(r) * length(c)

 

参考：

[1] Matlab绘制三维曲面（以二维高斯函数为例）（https://www.cnblogs.com/pzxbc/archive/2012/02/14/2351708.html）

 

---

在进行以上内容的学习时，也检索到下面的写得不错的博客：

（1）高斯函数以及在图像处理中的应用总结（https://www.cnblogs.com/herenzhiming/articles/5276106.html）

（2）高斯函数的详细分析（https://blog.csdn.net/jorg_zhao/article/details/52687448）