卷积神经网络(CNN)

1. CNN的起源

• 1962年，Hubel和Wiesel等通过对猫的大脑视觉皮层系统的研究，提出了感受野的概念，并进一步发现了视觉皮层通路中对于信息的分层处理机制，由此获得了诺贝尔生理学或医学奖。

  • Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. Journal of Physiology. 1962;160(1):106-154.

• 80年代中期，Fukushima等基于感受野概念提出的神经感知机（Neocognitron），可以看作是卷积神经网络的第一次实现，也是第一个基于神经元之间的局部连接性和层次结构组织的人工神经网络。神经认知机是将一个视觉模式分解成许多子模式，通过逐层阶梯式相连的特征平面对这些子模式特征进行处理，使得即使在目标对象产生微小畸变的情况下，模型也具有很好的识别能力。

  • Fukushima K, Miyake S. Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position. Pattern Recognition. 1982;15(6):455-69.

• 此后，研究人员开始尝试采用多层感知器（实际上是只含一层隐含层节点的浅层神经网络模型）来代替手工提取特征，并使用简单的随机梯度下降方法来训练该模型，1986年，Rumelhart，Hinton 和Williams 发表了著名的反向传播算法，这一算法随后被证明十分有效。

  • Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1986;323(6088):533-6.
  • Ruck DW, Rogers SK, Kabrisky M. Feature Selection Using a Multilayer Perceptron. Neural Network Computing. 1993;2:40-8.

• 1990年，Lecun等在研究手写数字识别问题时，首先提出了使用梯度反向传播算法训练的卷积神经网络模型，并在MNIST手写数字数据集上表现出了相对于当时其他方法更好的性能。

  • LeCun Y, Boser B, Denker J, Henderson D, Howard R. Handwritten digit recognition with a backpropogation network. World of Computer Science & Information Technology Journal. 1990;2:299-304. Available:

2. 概述

卷积神经网络(Convolutional Neural Network, CNN)是一种深层神经网络模型，它的特殊性体现在两个方面

• 相邻层的神经元间的连接是非全连接的
• 同一层中某些神经元之间的连接的权重是共享的

前馈神经网络每一层节点是一个线性的一维排列状态，层与层的网络节点之间是全连接的。这样设想一下，如果前馈网络中层与层之间的节点连接不再是全连接，而是局部连接的。这样，就是一种最简单的一维卷积网络。如果我们把上述这个思路扩展到二维，这就是我们在大多数参考资料上看到的卷积神经网络

① 局部连接

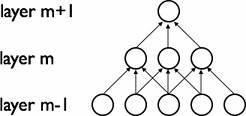
CNN在网络的相邻两层之间使用局部连接来获取图像的局部特性，具体来说，第m层的隐层单元只与第m-1层的局部区域有连接，第m-1层的这些局部区域被称为空间连续的接受域。如下图所示，其每一层接受域的宽度为3：

② 权值共享

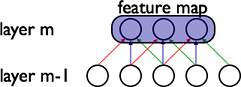
在CNN中，对整个图像进行一次卷积操作，不同局部区域使用的是同一个卷积核（即权重参数相同），由此生成了一个特征映射（feature map）。通过不同的卷积核对整个图像进行卷积可生成不同的 feature map。下图是一个权值共享的例子：

图中卷积核的接受域是3，同种颜色的连接代表相同的权重值，用一种卷积核进行卷积操作得到一个feature map

③ 例子

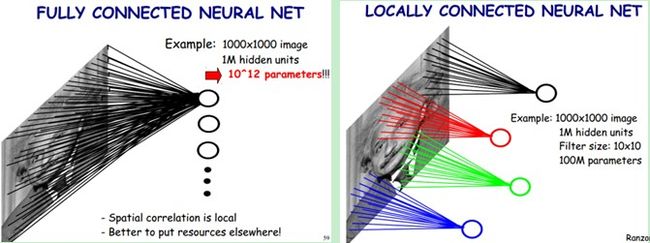
通过下图的例子进一步说明CNN的这两个特点：

左边这幅图是全连接网络。如果我们有1000x1000像素的图像，隐含层有1百万个神经元，每个神经元都连接图像的每一个像素点，就有1000x1000x1000000= 1012 个连接，也就有 1012 个权值参数

右边这幅图是局部连接网络，假如卷积核的窗口大小是10×10，隐含层每个神经元只需要和这10×10的局部图像相连接，所以1百万个隐含层神经元就只有1000000×10×10个连接，即 108 个参数，这就是局部连接。

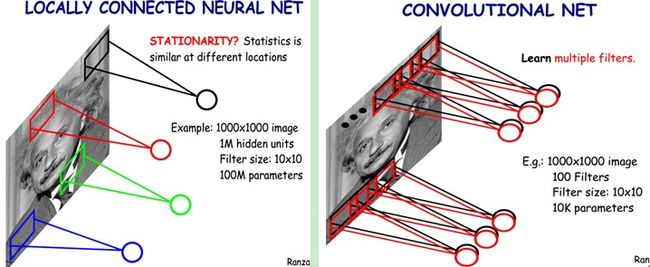
隐含层的每一个神经元都与大小为10×10的图像区域相连接，也就是说每一个神经元存在10×10=100个连接权重参数（卷积核参数）。如果每个神经元的连接权重参数相同，即每个神经元都使用同一个卷积核，这样整个网络就只有100个参数！这就是权值共享！

假如一种卷积核能够提出图像的一种特征，例如某个方向的边缘。如果我们需要提取不同的特征，就需要多使用几种卷积核。如下图所示，使用100种卷积核（不同卷积核的参数都不相同），每种卷积核代表对图像中不同特征的提取。

3. 卷积神经网络

卷积网络是为识别二维输入而特殊设计的一个多层感知器，这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。 这些良好的性能是网络在有监督方式下学会的，网络的结构主要有局部连接和权值共享两个特点，包括如下形式的约束：

1. 特征提取：每一个神经元从上一层的局部接受域得到突触输入，因而迫使它提取局部特征。一旦一个特征被提取出来， 只要它相对于其他特征的位置被近似地保留下来，它的精确位置就变得没有那么重要了。
2. 特征映射：网络的每一个隐含层都是由多个特征映射（feature map）组成的，每个特征映射都是二阶张量形式的。张量中的神经元共享同一种卷积核，这种结构形式具有如下的有益效果：a.平移不变性。b.自由参数数量的缩减(通过权值共享实现)。
3. 子采样（pooling）：每个卷积层后面跟着一个实现局部平均和子抽样的计算层，由此特征映射的分辨率降低。这种操作能够使特征映射的输出对平移和其他变形的敏感度下降。

① 卷积

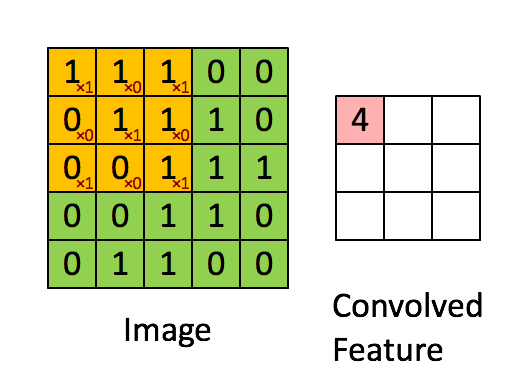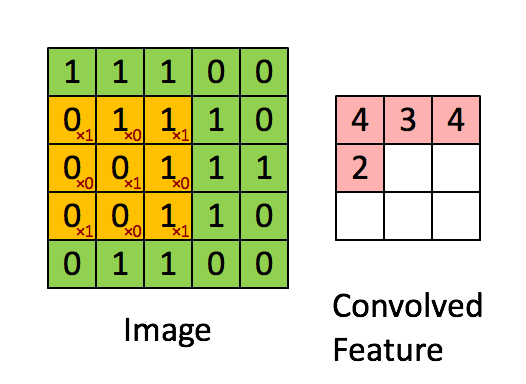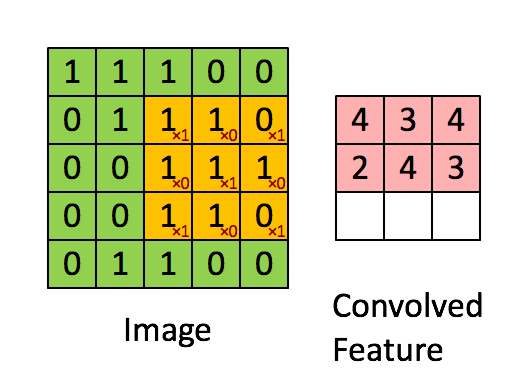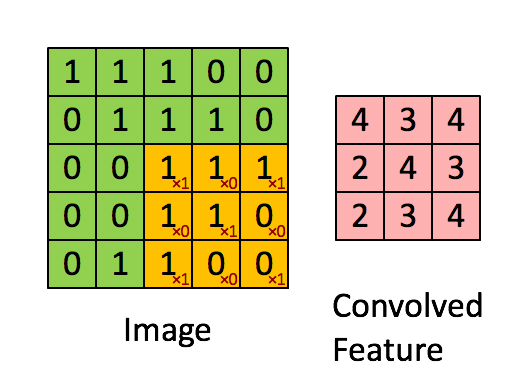
如下图所示，展示了一个3×3的卷积核在5×5的图像上做卷积的过程。左侧的绿色矩阵代表输入的一张图片（例如一张5px*5px的图片），3×3阶的黄色矩阵就是卷积核，用来提取图像的一种特征，让卷积核在图像上进行从左到右，从上到下移动。每移动一次，让卷积核与相应的图像局部区域做点积，就得到了右边矩阵中对应的一个元素。

每个卷积都是一种特征提取方式，通过一种特征提取可得到一个feature map。上图右边的3×3矩阵就是一个feature map，使用不同的卷积核可得到多种feature map

② 滑动的步长(stride)

步长(stride)决定了卷积核在移动过程中一次跳过几格。上面那张图片从左到右，每次滑动的时候只移动一格。

③ 卷积的边界处理(padding)

tensorflow中卷积的 padding参数可以设为两个值SAME，VALID

VALID模式如上图所示，对原始图像进行卷积，卷积后的矩阵只有3×3阶，比原来的图片要小了

SAME模式要求卷积后的feature map与输入的矩阵大小相同，因此需要对输入矩阵的外层包裹n层0，然后再按照VALID的卷积方法进行卷积。n的求法如下式：

• SAME：edge_row = (kernel_row - 1) / 2; edge_cols = (kernel_cols - 1) / 2;
• VALID：edge_row = edge_cols = 0;

其中，edge_row是包裹0的行数，edge_cols是包裹0的列数 , kernel_row就卷积核的行数

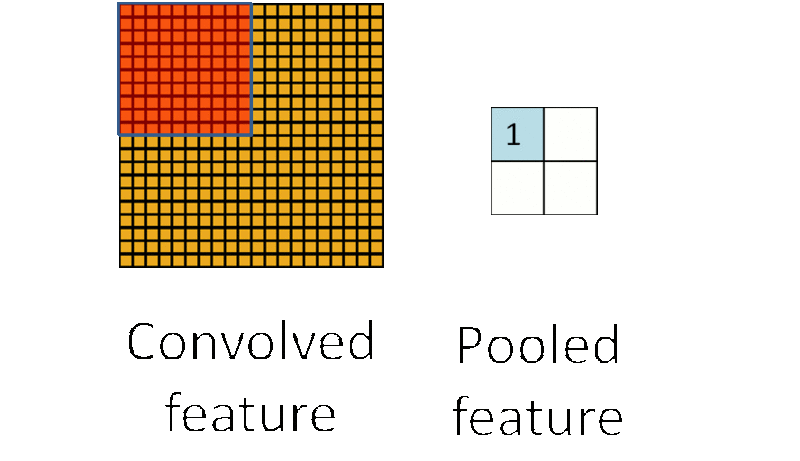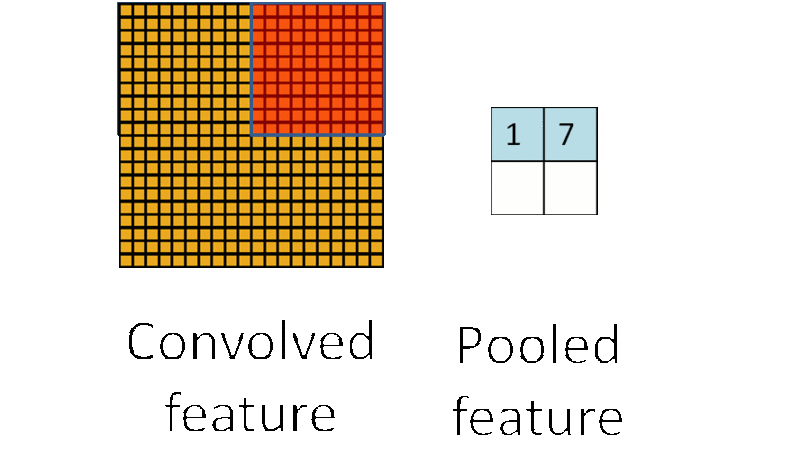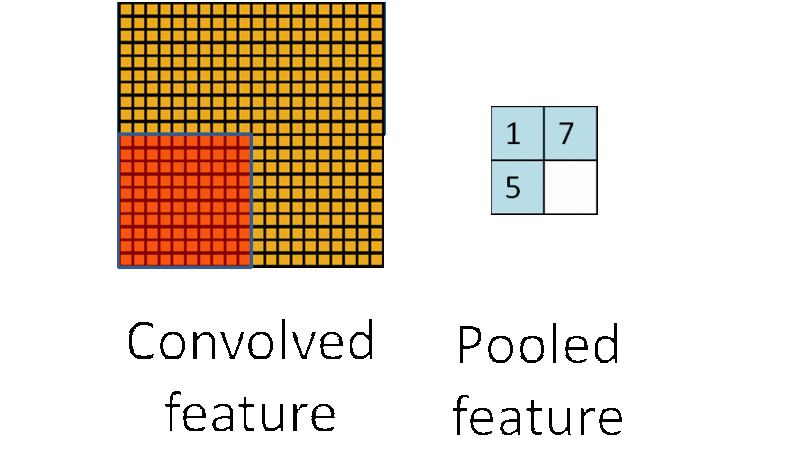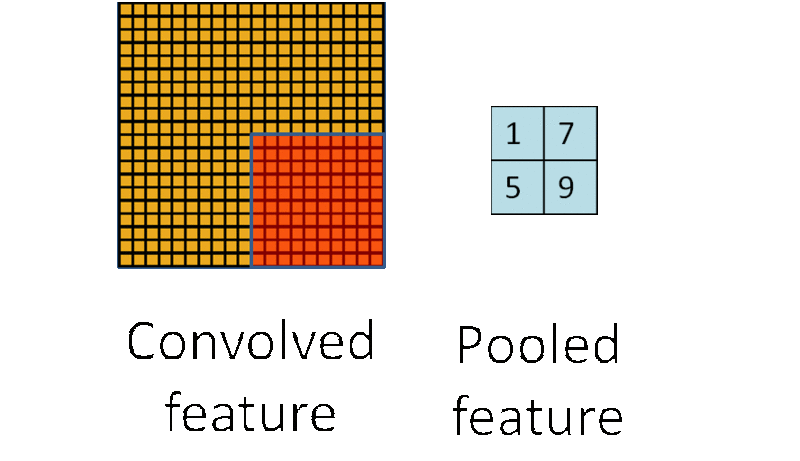
④ 池化(Pooling)

通过将卷积层提取到的特征输入至分类器中进行训练，可以实现输出最终的分类结果。理论上可以直接将卷积层提取到的所有特征输入至分类器中，然而这将需要非常大的计算开销。例如：对于一个输入为96×96大小的图像样本，假设在卷积层使用200个8×8大小的卷积核对该输入图像进行卷积运算操作，每个卷积核都输出一个（96-8＋1）×（96-8＋1）=7921维的特征向量，最终卷积层将输出一个7921×200=1584200维的特征向量。将如此高维度的特征输入至分类器中进行训练需要耗费非常庞大的计算资源，同时也会产生严重的过拟合问题。

由于图像具有 “静态性”，在图像的一个局部区域得到的特征极有可能在另一个局部区域同样适用。因此，可以对图像的一个局部区域中不同位置的特征进行聚合统计，这种操作称为“池化”(也称作子采样)。池化分为两种，一种是最大池化，在选中区域中找最大的值作为Pooling后的值，另一种是平均值池化，把选中的区域中的平均值作为Pooling后的值。

4 LeNet-5

LeNet-5是一个运用卷积神经网络进行手写数字识别的模型，LeNet-5的展示请参考：LeNet-5, convolutional neural networks

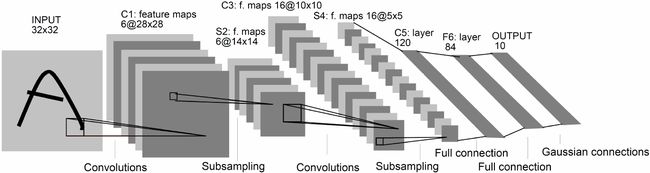
下图展示了LeNet-5的网络结构：

1. 输入层：输入图像大小为32 × 32 = 1024。
2. C1层：这一层是卷积层。滤波器的大小是5×5 = 25，共有6 个滤波器。得到6 组大小为28 × 28 = 784 的特征映射。因此，C1层的神经元个数为6 × 784 = 4, 704。可训练参数个数为6 × 25 + 6 = 156。连接数为156 × 784 = 122, 304（包括偏置在内，下同）。
3. S2 层：这一层为子采样层。由C1层每组特征映射中的2×2 邻域点次采样为1 个点，也就是4 个数的平均。这一层的神经元个数为14 × 14 = 196。可训练参数个数为6 × (1 + 1) = 12。连接数为6 × 196 × (4 + 1) = 122, 304 （包括偏置的连接）

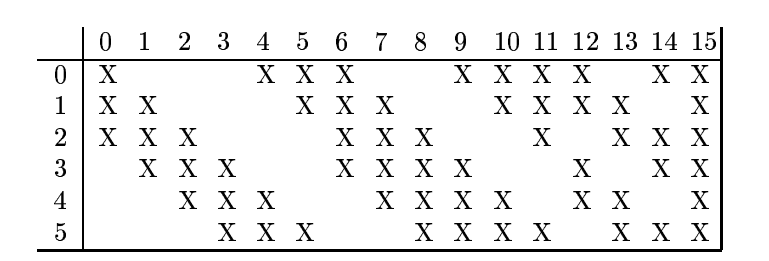
4. C3 层：这一层是卷积层。由于S2 层也有多组特征映射，需要一个连接表来定义不同层特征映射之间的依赖关系。LeNet-5 的连接表如下图所示，这样的连接机制的基本假设是：C3层的最开始的6 个特征映射依赖于S2层的特征映射的每3 个连续子集。接下来的6 个特征映射依赖于S2 层的特征映射的每4 个连续子集。再接下来的3 个特征映射依赖于S2 层的特征映射的每4 个不连续子集。最后一个特征映射依赖于S2 层的所有特征映射。这样共有60 个滤波器，大小是5 × 5 = 25。得到16 组大小为10×10 = 100 的特征映射。C3层的神经元个数为16×100 = 1, 600。可训练参数个数为(60 × 25 + 16 = 1, 516。连接数为1, 516 × 100 = 151, 600。

   

5. S4 层：这一层是一个子采样层，由2×2 邻域点次采样为1 个点，得到16 组5×5 大小的特征映射。可训练参数个数为16 × 2 = 32。连接数为16 × (4 + 1) = 2000。

6. C5 层：是一个卷积层，得到120 组大小为1 × 1 的特征映射。每个特征映射与S4层的全部特征映射相连。有120 × 16 = 1, 920 个滤波器，大小是5 × 5 = 25。C5层的神经元个数为120，可训练参数个数为1, 920 × 25 + 120 = 48, 120。连接数为120 × (16 × 25 + 1) = 48, 120。
7. F6层：是一个全连接层，有84个神经元，可训练参数个数为84×(120+1) = 10, 164。连接数和可训练参数个数相同，为10, 164。
8. 输出层：输出层由10 个欧氏径向基函数（Radial Basis Function，RBF）函数组成。

5 参考资料

1. CNN 其常见架构（上）
2. CNN 其常见架构（下）