java中的位运算

异或基本算法

  看题目顾名思义，泥瓦匠要跟你们聊聊这位运算。怎么聊法，依旧和老套。师傅出招棋盘上马，你徒弟怎么对答，然后周而复始。你就青出于蓝了。很早的时候在一本《算法竞赛入门经典》，有些acmer应该知道的。原题目很简单，是这样的：
两个变量A,B如何交换。
“定个temp不就搞定了。”骂声将至，我赶紧说，除了这个方法，还有下面这个：

< font  size="4" face="宋体">A = A + B;

B = A –B;

A = A - B;
font >

  这样子，我们不可全盘否认，在多数情况下，还是能达到目的的。但是问题就来了，这样做为什么不行呢。我们考虑下，一个是这试用的范围很小，不满足全部类型数据。二个是这个会越界，越界导致我们算法和程序会bug或者无法进行。
  又看看题目，聪明的小伙伴兴许想到了：

< font  size="4" face="宋体">private static void test1()
    {
        int A = 11;
        int B = 222;
        A = A ^ B;
        B = A ^ B;
        A = A ^ B;
    } font >

看着上面这个运算是CPU位运算，所以效率极高，也不会越界。在计算机系统中大量存在，可以反向规则恢复数据本身。这时候有些小伙伴不懂，泥瓦匠就补下异或的知识吧。

  异或运算，是按照二进制位进行。异或运算的规则是0⊕0=0,0⊕1=1，1⊕0=1,1⊕1=0。“这个也太烦了吧，记公式我最不行了。”这个也是来自前人，古人的武功秘籍。不是吗什么易筋经，什么少林武学。哈哈，太极啊，书法啊，要那个灵性，技巧。
  记忆宫殿：异或异或，又称半加法运算。例如，1⊕1可以当成二进下，1+1=10然后取最后一位，正好是异或的结果，0+0、1+1、0+1同理。这只是前人流传下来的记忆方法。

2.2.1 补充例子异或加密解密

  利用抑或算法进行加密解密。这是种简单加密，但是也有它的优势：速度快，长数据的一般加密任务很适合。不多说，代码如下：

/* encrypt using the exclusive or*/
    private static void test2(String str)
    {
        byte key = 123;
        byte strByte[] = str.getBytes();

        /* encrypt */
        for (int i = 0; i < strByte.length; i++)
        {
            strByte[i] = (byte) (strByte[i] ^ key);
        }

        System.out.println("加密后：" + new String(strByte));

        /* decrypt */
        for (int i = 0; i < strByte.length; i++)
        {
            strByte[i] = (byte) (strByte[i] ^ key);
        }

        System.out.println("解密后：" + new String(strByte));
    }

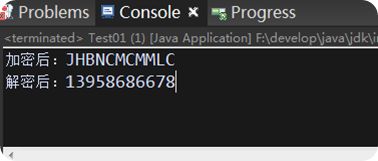
  我们测试下 test2("13958686678");，然后在控制台可以清楚的看出加密后和解密后的状态：

  总结：加密解密的操作方式一样，这个加密不怎么棒，而且一看数据都是对应的AABBCC型。但加密后的数据也可以进行存储或网络传输。如果有不需要很大安全性的，但是数据有长要求速度和效率的可以尝试下哦

2.3 ‘按位与’运算 就是那么简单

  下面要讲这个&了。上面讲了异或，下面我就讲讲这个，在很人眼里仿佛和异或有着某种，或是对立或是啥的关系的按位与运算符。其实没有，他们只是在CPU级别的，一些门电路设计下的规律而已。哈哈，虽然学过电子技术，但经常逃课，还挂科了，泥瓦匠也就不显摆我电子技术多牛逼了。举个例子吧：

    private static void test3()
{
    int a = 6550; //    1100110010110
    a = a & 255;  //         11111111
    System.out.println(a);// 10010110
}

  例子中，看了注释有些人懂了。其实例子很简单，就是一个数字截取二进制下从低到高的8位。和上面的一样，这运算符广泛的运用在系统内部。效率极高，但我们也可以在某种算法中去。比如我现在想要6550的二进制的不要二进制下从低到高的8位，那样你是否马上就能写出。只要把255改成（65535 - 255），然后右移8位即可呢？为什么是这个两个数字呢，告诉你转化成二进制你就明白了。

  按位与运算与（AND）：对两个整型操作数中对应位执行布尔代数，两个位都为1时输出1，否则0。
  这也没什么记忆技巧，一与一，唱着歌谣记下去。

2.4 从非中，学习原码补码运算

  累了累了，先去玩一会，再看下面很枯燥的东西吧。我推荐番茄工作法。25分钟。

  下面和你们一起学习这个枯燥的东西。要学习原码补码运算。首先得知道一些基础的东西：机器数和真值。所谓的机器数就是，一个数在计算机中的二进制形式。机器数时代符号的，在计算机用一个数的最高位存放符号。正数为0，负数为1。那什么叫真值呢？真值其实就是实际值，因为最高位的0或者1会导致形式上的有变，就像 1000 0011 表示机器数，它的真值为 –3 或者 -000 0001。哈哈？这个太简单的。对，什么事情都是简单到复杂。简单的事情做多了就成大事了。

  而原码, 反码, 补码是机器存储一个具体数字的编码方式。下面简单介绍这三个：
  原码是人最容易理解和计算的表达式。第一位表示符号，后面的表示值。0为正值，1为负值。
  反码，顾名思义，和原码有关系。有时候，一个反码表示负数，我们无法将其计算。可以转换为原码在计算。反码的计算方法如下：

      正数的反码是其本身

      负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

  补码的表达方式也如下：

      正数的补码就是其本身

      负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

   为什么要用这些呢。我的建议先死背，然后用领会。因为计算机里面最基础的运算需要他们帮助计算机完成。因为一个符号位正负会让基础电路设计很复杂。所以就想出来用符号位参与运算。反码，补码是用来计算用的。下面举个简单的例子。首先是反码计算十进制的表达式: 1-1=0。下面摘自网络大牛结论：

1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]_原和[1000 0000]_原两个编码表示0.

于是补码的出现, 解决了0的符号以及两个编码的问题:

1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原

这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]_补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]_原, 这是不正确的)

使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].

因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-2³¹, 2³¹-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.

2.5 综合算法现实案例

  最后一个综合性算法例子，就结束这篇位运算的文章。

  业务系统中，我们会发现大量的判定是否。以int数据为例子，如果按照十进制的方式存储数据，一个32位的int变量只能存储一个数值，而如果使用二进制方式存储数据(缺点是只能存储0或1两个数据)则可以存储32个数据，将极大的节约内存。利用位运算存储数据，主要是为了减少程序占用的内存。这样的设计是没有错的，但是如何操作呢？哈哈，泥瓦匠也不卖关子了。当然是位运算。但有些同学用什么toBinary转来转去，都不知道这样的操作复杂度很高，导致得不偿失。

所以设计好了，实现更重要

  例如，在一个int变量的从右侧开始倒数第5位存储数据，则存储和读取数据的代码如下所示： 

private static void test4()
    {
        //在一个int变量的从右侧开始倒数第5位存储数据
        int bData = 0;

        bData = bData | (1 << (5 - 1));    //存储数值1
        System.out.println(bData);

        bData = bData & (~(1 << (5 - 1))); //存储数值0
        System.out.println(bData);

        int n = bData & (1 << (5 - 1));    //读取数据
        System.out.println(n);
    }

  例子可以看出，我们成功的把5位的1和0互换。这就代表着一个是否的是否状态。所以泥瓦匠想说的是，考虑int的位而不是表面的意义能创造更多财富。财富来源于细节。和武学一样，最高境界就是 无形。但是要从有形来，组合的有形深不可测。就像这个综合案例一样。

    精髓：掌握到底层的妙用，方能成就高层建筑。