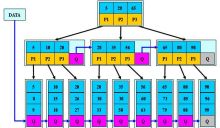
B+树

B+ 树是一种树数据结构，是一个n叉树，每个节点通常有多个孩子，一颗B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个 包含两个或两个以上孩子节点的节点。

B+ 树通常用于数据库和操作系统的 文件系统中。NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入。

中文名

B+树

外文名

B+ Tree

目录

1. 1 B+树
2. ▪ B+树的定义
3. ▪ B+树的查找
4. ▪ B+树的插入

1. ▪ B+树的删除
2. 2 B+树与B树的区别
3. 3 B+树与操作系统的文件索引和数据库索引

B+树编辑

B+树的定义

B+树是应 文件系统所需而出的一种 B-树的变型树。一棵m阶的B+树和m阶的B-树的差异在于：

1.有n棵子树的结点中含有n个 关键字，每个关键字不保存数据，只用来索引，所有数据都保存在叶子节点。

2.所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的 指针，且叶子结点本身依关键字的大小自小而大顺序链接。

3.所有的非终端结点可以看成是 索引部分，结点中仅含其子树（根结点）中的最大（或最小）关键字。

通常在B+树上有两个头指针，一个指向根结点，一个指向关键字最小的叶子结点。

B+树的查找

对B+树可以进行两种查找运算：

1.从最小关键字起 顺序查找；

2.从根结点开始，进行随机查找。

在查找时，若非终端结点上的关键值等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B+树中，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。其余同B-树的查找类似。

以下是从根节点查找叶子节点k的伪代码 [1]   ：

Function: search (k)
    return  tree_search (k, root); Function: tree_search (k, node)
    if  node is a leaf then         return  node;
    switch  k  do     case  k < k_0
        return  tree_search(k, p_0);
    case  k_i ≤ k < k_{i+ 1 }
        return  tree_search(k, p_{i+ 1 });
    case  k_d ≤ k
        return  tree_search(k, p_{d+ 1 });
//伪代码假设没有重复值

B+树的插入

m阶B树的插入操作在叶子结点上进行，假设要插入关键值a，找到叶子结点后插入a，做如下算法判别：

①如果当前结点是根结点并且插入后结点 关键字数目小于等于m，则算法结束；

②如果当前结点是非根结点并且插入后结点关键字数目小于等于m，则判断若a是新 索引值时转步骤④后结束，若a不是新索引值则直接结束；

③如果插入后关键字数目大于m(阶数)，则结点先分裂成两个结点X和Y，并且他们各自所含的关键字个数分别为：u=大于(m+1)/2的最小整数，v=小于(m+1)/2的最大整数；

由于索引值位于结点的最左端或者最右端，不妨假设索引值位于结点最右端，有如下操作：

如果当前分裂成的X和Y结点原来所属的结点是根结点，则从X和Y中取出索引的关键字，将这两个关键字组成新的根结点，并且这个根结点指向X和Y，算法结束；

如果当前分裂成的X和Y结点原来所属的结点是非根结点，依据假设条件判断，如果a成为Y的新 索引值，则转步骤④得到Y的双亲结点P，如果a不是Y结点的新索引值，则求出X和Y结点的双亲结点P；然后提取X结点中的新索引值a’，在P中插入 关键字a’，从P开始，继续进行插入算法；

④提取结点原来的索引值b，自顶向下，先判断根是否含有b，是则需要先将b替换为a，然后从根结点开始，记录结点地址P，判断P的孩子是否含有索引值b而不含有索引值a，是则先将孩子结点中的b替换为a，然后将P的孩子的地址赋值给P，继续搜索，直到发现P的孩子中已经含有a值时，停止搜索，返回地址P。

B+树的删除

B+树的删除也仅在叶子结点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于m/2 （m/2结果取 上界，如5/2结果为3）时，其和兄弟结点的合并过程亦和B-树类似。

B+树与B树的区别编辑

一棵m阶的B+树和m阶的B树的异同点在于：

• 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。(而B 树的叶子节点并没有包括全部需要查找的信息)
• 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。(而B 树的非终节点也包含需要查找的有效信息)

B+树与操作系统的文件索引和数据库索引编辑

为什么说B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引？ [2]  

• B+树的磁盘读写代价更低
  B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
  举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶 B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
• B+树的查询效率更加稳定
  由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

计算机科学中的树

二叉树	▪ 二叉树 ▪ 二叉查找树 ▪ 笛卡尔树 ▪ Top tree ▪ T树

自平衡二叉查找树	▪ AA树 ▪ AVL树 ▪ 红黑树 ▪ 伸展树 ▪ 树堆 ▪ 节点大小平衡树

B树	▪ B树 ▪ B+树 ▪ B*树 ▪ Bx树 ▪ UB树 ▪ 2-3树 ▪ 2-3-4树 ▪ (a,b)-树 ▪ Dancing tree ▪ H树

Trie	▪ 前缀树 ▪ 后缀树 ▪ 基数树

空间划分树	▪ 四叉树 ▪ 八叉树 ▪ k-d树 ▪ vp-树 ▪ R树 ▪ R*树 ▪ R+树 ▪ X树 ▪ M树 ▪ 线段树 ▪ 希尔伯特R树 ▪ 优先R树

非二叉树	▪ Exponential tree ▪ Fusion tree ▪ 区间树 ▪ PQ tree ▪ Range tree ▪ SPQR tree ▪ Van Emde Boas tree

其他类型	▪ 堆 ▪ 散列树 ▪ Finger tree ▪ Metric tree ▪ Cover tree ▪ BK-tree ▪ Doubly-chained tree ▪ iDistance ▪ Link-cut tree ▪ 树状数组

参考资料

• 1.  B+树  ．维基百科[引用日期2015-07-2]
• 2.  B+树  ．结构之法[引用日期2015-07-2]

词条标签：

计算机学