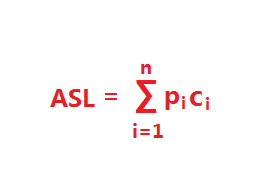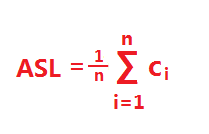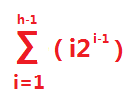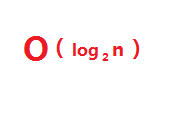顺序表查找(顺序查找、二分查找) C语言实现
1、基本概念
a. 从大量以前存储的数据中检索特定的一段信息或几段信息的操作称为查找或搜索。
b. 平均查找长度ASL的计算公式为:
其中,n 为查找表的长度(元素个数),pi 为查找第 i 个元素的概率,ci 是查找第 i 个元素时同给定值 K 所需比较的次数。
若查找每个元素的概率相同,则公式可简化为:
c. 顺序表:是指采用数组对集合或线性表进行顺序存储的结构形式。
在顺序表上进行查找又多种方法,这里只介绍最主要的两种方法:顺序查找和二分查找。
2、顺序查找
顺序查找是一种最简单和最基本的查找方法,它从顺序表的一端开始,依次将每个元素的关键字同给定值 K 进行比较,直到相等或比较完毕还未找到。算法如下:
int Seqsch(struct ElemType A[], int n, KeyType K)
{
int i;
for (i = 0; i < n; i++)
if (A[i].key == K)
break;
if (i < n)
return i;
else
return -1;
}其中,顺序表采用一堆数组 A 表示,其元素类型为 ElemType ,它含有关键字 key 域和其他一些数据域,key 域类型用标识符 KeyType 表示,线性表长度为 n(元素个数)
改进: 可以把给定值 K 赋给数组 A 中第 n 个位置,这样无需数组比较,只需元素比较,而且比较到第 n 位置时,A[n].key == K 必然成立,将自动结束循环。算法如下:
int Seqsch1(struct ElemType A[], int n, KeyType K)
{
int i;
A[n].key = K; //设置岗哨
for (i = 0; ; i++)
if (A[i].key == K)
break;
if (i < n)
return i;
else
return -1;
}顺序查找分析:
缺点是速度慢,平均查找长度为 (n + 1) / 2,时间复杂度为 O(n) .
优点是即适用于顺序表,也适用于单链表,同时对表中元素排列次序无要求,给插入和删除元素带来了方便。
3、二分查找
二分查找又称折半查找。
作为二分查找对象的表必须是顺序存储的有序表,通常假定有序表是按关键字从小到大有序。
查找过程是首先取整个有序表 A[0] ~ A[n - 1] 的中点元素 A[mid] (mid = (0 + n -1) / 2) 的关键字同给定值 K 比较,相等则成功,若 K 较小,则对 剩余的左半部分进行同样
操作,若 K 较大,则对其剩余的右半部分进行同样的操作。算法如下(分为递归和非递归两种算法):
int Binsch(struct ElemType A[], int low, int high, KeyType K)//递归法
{//在 A[low] ~ A[hight]区间进行查找,low、hight初值分别为 0 和 n-1
if (low <= hight)
{
int mid = (low + high) / 2; //求中点元素下标
if (K == A[mid].key)
return mid;
else if (K < A[mid].key)
return Binsch(A, low, mid - 1, K);
else
return Binsch(A, mid + 1, high, K);
}
else
return -1; //查找失败
}
int Binsch1(struct ElemType A[], int low, int high, KeyType K)//非递归法
{//在 A[low] ~ A[hight]区间进行查找,low、hight初值分别为 0 和 n-1
if (low <= hight)
{
int mid = (low + high) / 2; //求中点元素下标
if (K == A[mid].key)
return mid;
else if (K < A[mid].key)
high = mid - 1;
else
low = mid + 1;
}
else
return -1; //查找失败
}二分查找分析:
二分查找可以用判定树描述,二分查找的判定树不仅是一棵二叉搜索树,而且还是一棵理想平衡树。
判定树的高度 h 和结点数 n 的关系为:
判定树为理想平衡树,所以前 h-1 层都是满的,在前 n-1 层中查找所有元素的比较次数之和为 :
在第 h (最后一层)层中查找所有元素的比较次数之和为 :
可得进行二分查找的平均查找长度为:
时间复杂度为:
二分查找的优点是比较次数少,速度快,但在查找之前要为建立有序表付出代价,同时对有序表的插入和删除也较为费力。
二分查找适用于数据相对稳定的情况,而且只适用于顺序存储的有序表,不适用链接存储的有序表。