无监督学习——关联分析
1.1. 关联分析
1.1.1. Apriori算法(先验算法)
关联分析(Association Analysis):在大规模数据集中寻找有趣的关系。
频繁项集(Frequent Item Sets):经常出现在一块的物品的集合。
关联规则(Association Rules):暗示两个物品之间可能存在很强的关系。
支持度(Support):数据集中包含该项集的记录所占的比例,是针对项集来说的。
例子:豆奶,橙汁,尿布和啤酒是超市中的商品。
下表呈现每笔交易以及顾客所买的商品:
项集 |
商品 |
1 |
豆奶、橙汁 |
2 |
尿布、啤酒 |
3 |
橙汁、豆奶、尿布、啤酒 |
4 |
橙汁、豆奶、啤酒 |
5 |
尿布、啤酒 |
由此可见,总记录数为5,下面求每项集的支持度(以下并没有列出全部的支持度)。
{豆奶} :支持度为3/5.
{橙汁}:支持度为3/5.
{尿布}:支持度为3/5.
{啤酒}:支持度为4/5.
{啤酒,尿布}:支持度为3/5.
{橙汁,豆奶,啤酒}:支持度为2/5.
置信度(Confidence):出现某些物品时,另外一些物品必定出现的概率,针对规则而言。
规则1:{尿布}-->{啤酒},表示在出现尿布的时候,同时出现啤酒的概率。
该条规则的置信度被定义为:支持度{尿布,啤酒}/支持度{尿布}=(3/5)/(3/5)=3/3=1
规则2:{啤酒}-->{尿布},表示在出现啤酒的时候,同时出现尿布的概率。
该条规则的置信度被定义为:支持度{尿布,啤酒}/支持度{啤酒}=(3/5)/(4/5)=3/4
关联分析步骤:
一、发现频繁项集:即计算所有可能组合数的支持度,找出不少于人为设定的最小支持度的集合。
项集 |
商品 |
编码 |
1 |
豆奶、橙汁 |
0,1 |
2 |
尿布、啤酒 |
2,3 |
3 |
橙汁、豆奶、尿布、啤酒 |
0,1,2,3 |
4 |
橙汁、豆奶、啤酒 |
0,1,3 |
5 |
尿布、啤酒 |
2,3 |
共2^n-1=15种组合
组合 |
支持度 |
0 |
3/5 |
1 |
3/5 |
2 |
3/5 |
3 |
4/5 |
01 |
3/5 |
02 |
1/5 |
03 |
2/5 |
12 |
1/5 |
13 |
2/5 |
23 |
3/5 |
012 |
1/5 |
013 |
2/5 |
023 |
1/5 |
123 |
1/5 |
0123 |
1/5 |
如果设定最小支持度为2/5,那么就能筛选出频繁项集。
二、发现关联规则:即计算不小于人为设定的最小支持度的集合的置信度,找到不小于认为设定的最小置信度规则。
筛选出的频繁项集及频繁项集对应的规则为:
组合 |
支持度 |
规则 |
0 |
3/5 |
-- |
1 |
3/5 |
-- |
2 |
3/5 |
-- |
3 |
4/5 |
-- |
01 |
3/5 |
2条 |
03 |
2/5 |
2条 |
13 |
2/5 |
2条 |
23 |
2/5 |
2条 |
013 |
2/5 |
6条 |
最小置信度:3/4 |
||
输出强关联规则:
最后可以得到:
0->1(支持度{0,1}/支持度{0}=(2/5) / (2/5)=1)
1->0(支持度{0,1}/支持度{1}=(2/5) / (2/5)=1)
2->3(支持度{2,3}/支持度{2}=(3/5) / (3/5)=1)
3->2(支持度{2,3}/支持度{3}=(3/5) / (4/5)=3/4)
13->0(支持度{0,1,3}/支持度{1,3}=(2/5) / (2/5)=1)
03->1(支持度{0,1,3}/支持度{0,3}=(2/5) / (2/5)=1)
6条强关联规则。
缺点
(1)在每一步产生侯选项目集时循环产生的组合过多,没有排除不应该参与组合的元素;
(2)每次计算项集的支持度时,都对数据库D中的全部记录进行了一遍扫描比较,如果是一个大型的数据库的话,这种扫描比较会大大增加计算机系统的I/O开销。而这种代价是随着数据库的记录的增加呈现出几何级数的增加。
1.1.2. FP-growth算法
FP-growth算法能够高效的发现频繁项集,但不能用于发现关联规则。FP-growth算法只需要对数据库进行两次扫描,而Apriori算法对每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁。
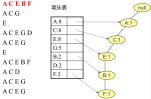
1. 建立项头表:
第一列数据:就是原始数据,A B C E F O,就可以理解为上一章中例子,购物时客户买了橙汁、豆奶、尿布、啤酒等;
第二列数据项头表:第一次扫描数据库后得到的支持度大于20%的单项集;
第三列数据:对于该项数据剔除支持度低的单项集,并且按支持度排序后的这一项;
2. FP-Tree建立
插入时按照排序后的顺序,首先插入第一条数据A C E B F,以此类推见下图:
3. FP-Tree挖掘频繁项集
首先从项头表底部依次向上挖掘。对于项头表对应于FP树的每一项,找到它的条件模式基。
为了介绍条件模式基,我们首先挖掘D节点:
Ø 找到以D结尾的路径:{A:8,C:8,E:6,G:4,D:1}、{A:8,C:8,D:1},代表的意义是:原数据集中{A,C,E,G,D}、{A,C,D}各出现依次。
Ø D的两个前缀路径{(A,C,E,G):1,(A,C):1}构成了D的条件模式基;
Ø 因为E,G只出现一次,所以E,G是非频繁项集,删除;
Ø 得到条件频繁项集{A:2,C:2};
Ø 通过它,我们得到D的频繁2项集为{A:2,D:2}、{C:2,D:2},频繁3项集{A:2,C:2,D:2}。
挖掘F节点:
Ø 找到以F结尾的路径:{A:8,C:8,E:6,B:2,F:2},代表的意义是:原数据集中{A,C,E,B,F}出现过两次;
Ø F的前缀路径{(A,C,E,B):2}构成F 的条件模式基;
Ø 得到频繁项集{A:2,C:2,E:2,B:2};
Ø 得到频繁2项集为{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,F:2},{A:2,E:2,F:2},...还有一些频繁三项集,就不写了。当然一直递归下去,最大的频繁项集为频繁5项集,为{A:2,C:2,E:2,B:2,F:2}。
以下流程省略,得到G的条件模式基{A:5,C:5,E:4};E的条件模式基{A:6,C:6};C的条件模式基{A:8}。
FP Tree算法改进了Apriori算法的I/O瓶颈,巧妙的利用了树结构,这让我们想起了BIRCH聚类,BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。
在实践中,FP Tree算法是可以用于生产环境的关联算法,而Apriori算法则做为先驱,起着关联算法指明灯的作用。除了FP Tree,像GSP,CBA之类的算法都是Apriori派系的。