等价:
设 R 是某个集合 A 上的一个二元关系。若 R 满足以下条件：
- 自反性：
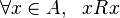
- 对称性：
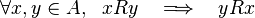
- 传递性：
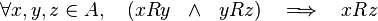
则称 R 是一个定义在 A 上的等价关系。习惯上会把等价关系的符号由 R 改写为 ∼。
例如，设 
，定义A上的关系R如下：
其中
叫做 x 与 y 模 3 同余，即 x 除以 3 的余数与 y 除以 3 的余数相等。例子有 1R4, 2R5, 3R6。不难验证 R 为 A 上的等价关系。
不是所有的二元关系也是等价关系。一个简单的反例子是比较两个数中哪个较大：
- 没有自反性：任何一个数不能比自身为较大 (
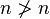) - 没有对称性：如果 m > n，就肯定不能有 n > m
偏序是在集合 P 上的二元关系 ≤，它是自反的、反对称的、和传递的，就是说，对于所有 P 中的 a, b 和 c，有着:
- a ≤ a (自反性)；
- 如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)；
- 如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性)。
带有偏序的集合叫做偏序集合(也叫做 poset)。术语有序集合有时也用于偏序集合，只要上下文中不涉及其他种类的次序。特别是，全序集合也可以被称为是"有序集合"，特别是在这些结构比偏序集合更常用的领域内。
偏序
设A是一个非空集，P是A上的一个关系，若关系P是 自反的、 反对称的、和 传递的，则称P是集合A上的偏序关系。(#add和等价的区别在于反对称)即P适合下列条件：
（1）对任意的a∈A,(a,a)∈P;
（2）若（a,b)∈P且（b,a)∈P,则a=b;
（3）若（a,b)∈P,(b,c)∈P,则（a,c)∈P,则称P是A上的一个偏序关系。带偏序关系的集合A称为偏序集或半序集。
若P是A上的一个偏序关系，我们用a≤b来表示（a,b)∈P。
举如下例子说明偏序关系：
1、实数集上的小于等于关系是一个偏序关系。
2、设S是集合，P（S）是S的所有子集构成的集合，定义P（S）中两个元素A≤B当且仅当A是B的子集，即A包含于B，则P（S）在这个关系下成为偏序集。
3、设N是正整数集，定义m≤n当且仅当m能整除n，不难验证这是一个偏序关系。注意它不同于N上的自然序关系。
全序
在集合A中，如果对于任意a∈A, b∈A, 有aRb或bRa，即A中的每对元素都满足关系R，则集合A上的偏序R是全序的或线性序的。
以上讲的过于科学，本人看不懂在折腾了好长一段时间终于搞明白了原来就是这么个事
a,b是书上的例图，分别代表偏序，全序，右下角那么嘛~~~~~逗乐~~~(*^__^*)
来看a图
按照正常遍历那么有2种路径，分别为1234,1324，2和3之间无法判断谁前谁后,而其他则可以判断前后顺序，比如1始终在2，3遍历之前。2和3始终在4之前
那2和3呢？无法判断，所以这就是偏序，此时2和3因没有顺序，整个是部分有序；再看图b在2和3之间加了一个指向，由2指向3，所以路线只有1234，