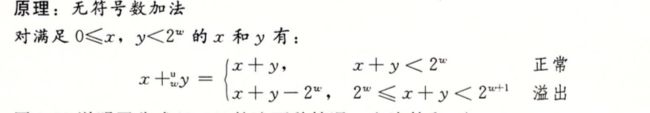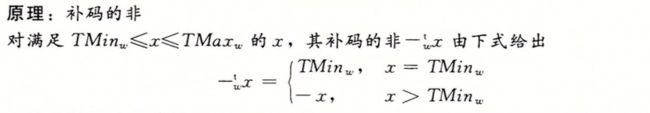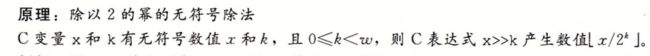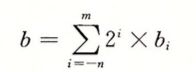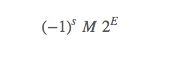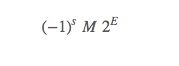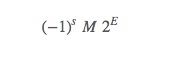本应该之前整理好的,又拖到现在,不管怎么样继续坚持看下去,从二章开始就越来越不好理解了
整数运算
再次来看之前的一个例子:
root@localhost: lldb (lldb) print (500 * 400) * (300 * 200) (int) $0 = -884901888 (lldb) print ((500 * 400)* 300) * 200 (int) $1 = -884901888 (lldb) print ((200 * 500) * 300) * 400 (int) $2 = -884901888 (lldb) print 400 * (200 * (300 * 500)) (int) $3 = -884901888 (lldb)
还是通过这里例子来看这个部分的知识点
无符号加法
无符号加法原理:
其实每次看到这种原理推导过程自己基本都不怎么愿意去看,不过我们可以通过实际的例子来好好理解,来帮助自己更好的理解
通过一个确定的4位的无符号数来看,如果x = 9 y = 12 x和y的二进制表示分别为[1001] 和 [1100] 他们相加的和为21 这个时候其实超过了我们最开始设定的4位,需要用5位来表示也就是[10101] 如果我们丢掉了最高位,就成了[0101] 转换为十进制就是5 其实这个值的计算结果就是21 对16 求余 得到5是一致的
这个时候我们在来看上面的公式原理,其实就是当你两个数相加已经超过了最大位数的时候,最高位就会被舍弃,即当结果溢时需要舍弃最高位的值
无符号求反
还是先看原理:
这里其实我自己有点小疑惑,因为刚开始的时候,我理解的无符号数求反,是把一个数的二进制表示方式求反得到的值,这样吧,通过一个实际的例子来理解:
对于12 二进制为[1100] 我理解的求反得到的是[0011]这样得到的数是3
但是这里讲的无符号数求反,其实是通过2的4次方 减去 12 得到的是 4
所以这里有点不确定,这个求反,后续再查资料看看是怎么回事
补码加法
这里第一次看的时候没有理解,不过后来又过了几天再看了一下理解了(可能之前看的时候,一眼看去都是公式,自己就不想看)
既然是补码的加班,先回顾一下补码的最大值和最小值
对于一个w为的补码数来说,能表示的最小值为:-2的w-1次方, 表示的最大值为:2的w-1次方 减1
在给定范围x>=-2的w-1次方, y <= 2的w-1次方减1 它们的和的范围就是-2的w次方<=x+y<=2的w次方减2
来吧,先看一下原理:
当x+y的值超过的补码的最大值的时候即大于TMax的时候是正溢出,需要减去2的w次方
当x+y的值小于补码的最小值的时候即小于Tmin的时候是负溢出,需要加上2的w次方
补码的非
还是先看原理:
其实对于补码的非有个简单的方法
先看几个实际的例子:
总结为一句话就是:对每一位求补,在对其结果加1
其实还有一种方法,还是通过一些例子理解:
其实总结一下就是:找到最右边的1,然后这个1的左边的所有位进行取反
无符号乘法
无符号的最大值的表示是2的w次方减1,那么对于x >=0 y <= 2的w次方减1,x和y的乘积的取值范围就是0到 (2的w次方减1)的平方, 这样可能就会需要2w位来表示,C语言中的无符号乘法被定义为产生w为的值,就是2w位的整数乘积的低w位表示的值
来看看原理为:
补码乘法
还是先看原理:
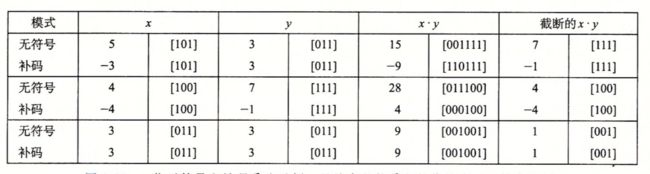
其实对于无符号和补码乘法来说乘法的位级运算都是一样的
通过下面这个实际的例子,就会更加清楚:
乘以2的幂
早些时候,在大多数机器上,整数的乘法指令是非常慢的,所以编译器对此作了优化,通过位移和加法运算的组合方式来代替乘以常数因子的乘法
原理如下:
一般原理看起来都不容易理解,或者估计很多人和我刚开始看的时候一样也是直接忽略,所以还是结合例子来看:
还是以w=4来看,即4位, 11可以通过二进制[1011]表示,k=2 时,将其左移到6位向量得到[101100],即编码为无符号数11*4 = 44
无论是无符号运算还是补码运算,乘以2的幂都可以能会导致溢出。但是即使溢出的时候,通过位移得到的结果也是一样的
由于整数乘法比位移和加法的代价要大的多,许多c语言编译器试图以位移、加法和减法的组合来消除很多整数乘以常数的情况,一个例子:
x * 14 利用14 = 2的3次方 + 2的2次方 + 2的1次方 编译器会讲乘法重写为(x<<3) + (x<<2) + (x<<1)
无论x是无符号还是补码,甚至当乘法会导致溢出时,两个计算都会得到一样的结果
设置编译器还可以利用14 = 2的4次方 - 2的1次方 将乘法重写为(x<<4)-(x<<1)
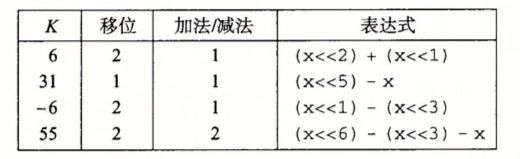
下面是一个例子:
中间的移位表示要有几个移位,后面的加法/减法表示做几次加法或者减法
除以2的幂
大多数机器上,整数除法要比整数乘法更慢,需要30个或者更多的时钟周期
除以2的幂也可以用移位运算来实现,不过这里用的是右移,而不是左移
无符号和补码分别使用逻辑移位和算数移位来达到目的
来看原理:
下面是在12340的16位表示上执行逻辑右移的结果对它执行逻辑右移的结果,以及对它执行除以1,2,16,和256的结果
当x>=0, 变量x的最高有效位为0,所以效果与逻辑右移是一样的,因此对于非负数来说,算术右移k位,和除以2的k次方是一样的
下图是-12340的16位表示进行算术右移不同位数的结果。对于不需要舍入的情况结果是x/2的k次方
当时当需要进行舍入的时候,位移导致结果向下舍入入右移4位会把-771.25向下舍入为-772
关于除以2的幂的补码除法,向上舍入不是非常理解,后面需要再看
在执行算术右移之前加上一个适当的偏执量来修正舍入,看下图:
在第三列,给出了-12340加上偏量值之后的结果,低k位以斜体表示,可以看出,低k位左边的位可能会加1,也可能不会加1,对于不需要舍入的情况k=1,加上偏量只会影响那些被移掉的位,对于需要舍入的情况,加上偏量导致较高的位加1,所以结果会向零舍入
关于整数运算的小结
计算机执行的整数运算实际上是一种模运算形式,表示数字的有限字长限制了可能的值的取值范围,结果可能溢出。
同时补码表示还提供了一种既能表示负数,也能表示正数的灵活方法,使用了与执行无符号算术相同的位级实现,包括:加法,减法,乘法,除法,无论运算是以无符号形式还是以补码形式,都完全一样活着非常类似的位级行为
浮点数
浮点数可以用统一的公式表示:
如:
并且可以看到除以2 就相当于右移,并且可以横跨小数点
当时这种表示是有问题的,如:x/2的k次方的数可以精确表示,其他数字会变成循环小数
如1/3 = 0.0101010101[01]....
IEEE浮点数标准
IEEE标准中,用下面公式表示浮点数
符号(sign):s是符号位,决定正负
尾数(singificand):M是一个二进制小数,它的范围通常是[1.0,2.0]
阶码(exponent):E 的作用是对浮点数加权,这个权重是2的E次幂
其中 s 对应着符号位,exp 对应着 E,frac 对应着 M。不同的位数就代表了不同的表示能力,也就是单精度,双精度,扩展精度的来源。
规范化值
在 exp≠000…0 和 exp≠111…1 时,表示的其实都是规范化的值
再来看公式:
这里的 E 是一个偏移的值 E=Exp−Bias
Exp: 是 exp 编码区域的无符号数值
Bias:值为 2的k-1次方−1 的偏移量,其中 k 是 exp 编码的位数,也就是说
单精度:127(Exp: 1…254, E: -126…127)
双精度:1023(Exp: 1…2046, E: -1022…1023)
之所以需要采用一个偏移量,是为了保证 exp 编码只需要以无符号数来处理。
而对于 M,一定是以 1 开头的:也就是 M=1.xxx…x。其中 xxx 的部分就是 frac 的编码部分,当 frac=000.00 的时候值最小(M=1.0),当 frac=111。。。1 的时候值最大(M=2.0−ϵ)
一个例子:
float F = 15213.0
用上面方法理解:
15213=11101101101101=1.1101101101101×2的13次方
于是 frac 部分的值就是小数点后面的数值,而 Exp = E + Bias = 13 + 127 = 140 = 10001100,于是编码出来的浮点数是这样的:
0 10001100 11011011011010000000000
s exp frac
非规范化值
当 exp=000…0 的时候,值是非规范化的,意思是,虽然实数轴上原来连续的值会被规范到有限的定值上,但是并些定值之间的间距也是一样的
和前面不同的是
E=1−Bias
而且 M=0.xxx…x,不是以 1 开头了。
当 exp=000…0 且 frac = 000…0 时,表示 0,而且因为符号位的缘故,实际上是有 +0 和 -0 两种的。而在 exp=000..0 且 frac≠000…0 时,数值是接近 0 的,并且间距是一致的
特殊值
还有一种特殊情况,就是 exp=111…1 时,表示一些特殊值。
当 exp=111…1 且 frac = 000…0 时,表示 ∞,而且因为符号位的缘故,实际上是有 +∞ 和 −∞ 两种的。那些会溢出的操作就会用这个来表示,比如 1.0/0.0=−1.0/0.0=+∞,1.0/−0.0=−∞
而在 exp=111…1 且 frac≠000…0 时,我们认为这不是一个数值(Not-a-Number,NaN),用来表示那些没办法确定的值,比如 sqrt(−1),∞−∞,∞×0
通过例子理解:
接下来举一个实际的例子,我们采用 1 位符号位,4 位 exp 位,3 位 frac 位,因此对应的 bias 为 7。回顾一下几个重要公式:
对于规范化数:E=Exp−Bias;对于非规范数:E=1−Bias,正数部分的数值为
s exp frac E 值 ------------------------------------------------------------------ 0 0000 000 -6 0 # 这部分是非规范化数值,下一部分是规范化值 0 0000 001 -6 1/8 * 1/64 = 1/512 # 能表示的最接近零的值 0 0000 010 -6 2/8 * 1/64 = 2/512 ... 0 0000 110 -6 6/8 * 1/64 = 6/512 0 0000 111 -6 7/8 * 1/64 = 7/512 # 能表示的最大非规范化值 ------------------------------------------------------------------ 0 0001 000 -6 8/8 * 1/64 = 8/512 # 能表示的最小规范化值 0 0001 001 -6 9/8 * 1/64 = 9/512 ... 0 0110 110 -1 14/8 * 1/2 = 14/16 0 0110 111 -1 15/8 * 1/2 = 15/16 # 最接近且小于 1 的值 0 0111 000 0 8/8 * 1 = 1 0 0111 001 0 9/8 * 1 = 9/8 # 最接近且大于 1 的值 0 0111 010 0 10/8 * 1 = 10/8 ... 0 1110 110 7 14/8 * 128 = 224 0 1110 111 7 15/8 * 128 = 240 # 能表示的最大规范化值 ------------------------------------------------------------------ 0 1111 000 n/a 无穷 # 特殊值
从上面可以看出:
在 exp=0000 时,也就是非规范化的情况,间距是一致的,都是 1/8
因为位数的限制,从零到一之间的数字只能以 1/8 为最小单位来表示,且相邻数字间间距一样
在规范化的部分,可以发现由于 exp 部分的不同,所以相邻数字间的间隔也是不同的,比方说最接近 1 的数字是 15/16 和 9/8,分别相差 1/16 和 1/8,这也是由于 IEEE 浮点数表示法的公式决定的
舍入
对于浮点数的加法和乘法来说,我们可以先计算出准确值,然后转换到合适的精度。在这个过程中,既可能会溢出,也可能需要舍入来满足 frac 的精度。
在二进制中,我们舍入到最近的偶数,即如果出现在中间的情况,舍入之后最右边的值要是偶数,对于十进制数,例子如下:
原数值 舍入结果 原因 2.8949999 2.89 不到一半,正常四舍五入 2.8950001 2.90 超过一半,正常四舍五入 2.8950000 2.90 刚好在一半时,保证最后一位是偶数,所以向上舍入 2.8850000 2.88 刚好在一半时,保证最后一位是偶数,所以向下舍入
小结
计算机将信息编码为位(比特),通常组织成字节序列。不同的编码方式用来表示整数,实数和字符串
大多数机器对整数使用补码编码,对于浮点数使用IEEE标准编码
由于编码的长度有限,计算机运算具有不同的属性,当超过表示范围时,有限长度能够引出数值溢出。
当浮点数非常接近0.0 从而转换为0时,也会下溢
整体上第二章花了很多时间看,但是其实对很多知识还是没有做到完全理解,后面可以回过头重新来看,可能那个时候会有新的理解,也能更加深刻