[vins-mono代码阅读]边缘化

先记住这张图，特别好，这张图中将所有的参数块变量和约束因子根据待marg的变量分为不同的组，在边缘化过程中，我们只需要关注处理下图中的xm,xb,zc的信息。

class ResidualBlockInfo

struct ResidualBlockInfo
{
    ResidualBlockInfo(ceres::CostFunction *_cost_function, ceres::LossFunction *_loss_function, std::vector<double *> _parameter_blocks, std::vector<int> _drop_set)
        : cost_function(_cost_function), loss_function(_loss_function), parameter_blocks(_parameter_blocks), drop_set(_drop_set) {}

    void Evaluate();

    ceres::CostFunction *cost_function;
    ceres::LossFunction *loss_function;
    std::vector<double *> parameter_blocks;
    std::vector<int> drop_set;

    double **raw_jacobians;
    std::vector<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobians;
    Eigen::VectorXd residuals;

    int localSize(int size)
    {
        return size == 7 ? 6 : size;
    }
};

类描述：这个类保存了待marg变量（xm）与相关联变量（xb）之间的一个约束因子关系。
部分成员变量描述：

成员变量	描述
cost_function	对应ceres中表示约束因子的类
parameter_blocks	该约束因子相关联的参数块变量
drop_set	parameter_blocks中待marg变量的索引

class MarginalizationInfo

class MarginalizationInfo
{
  public:
    ~MarginalizationInfo();
    int localSize(int size) const;
    int globalSize(int size) const;
    void addResidualBlockInfo(ResidualBlockInfo *residual_block_info);
    void preMarginalize();
    void marginalize();
    std::vector<double *> getParameterBlocks(std::unordered_map<long, double *> &addr_shift);

    std::vector<ResidualBlockInfo *> factors;
    //这里将参数块分为Xm,Xb,Xr,Xm表示被marg掉的参数块，Xb表示与Xm相连接的参数块，Xr表示剩余的参数块
    //那么m=Xm的localsize之和，n为Xb的localsize之和，pos为（Xm+Xb）localsize之和
    int m, n;      
    std::unordered_map<long, int> parameter_block_size; //global size 将被marg掉的约束边相关联的参数块，即将被marg掉的参数块以及与它们直接相连的参数快
    int sum_block_size;
    std::unordered_map<long, int> parameter_block_idx; //local size  
    std::unordered_map<long, double *> parameter_block_data;

    std::vector<int> keep_block_size; //global size
    std::vector<int> keep_block_idx;  //local size
    std::vector<double *> keep_block_data;

    Eigen::MatrixXd linearized_jacobians;
    Eigen::VectorXd linearized_residuals;
    const double eps = 1e-8;

};

类描述：这个类保存了优化时上一步边缘化后保留下来的先验信息。
成员变量信息：

成员变量	描述
factors	xm与xb之间的约束因子
m	所有将被marg掉变量的localsize之和，如上图中xm的localsize
n	所有与将被marg掉变量有约束关系的变量的localsize之和，如上图中xb的localsize
parameter_block_size	<参数块地址，参数块的global size>，参数块包括xm和xb
parameter_block_idx	<参数块地址，参数块排序好后的索引>，对参数块进行排序，xm排在前面，xb排成后面，使用localsize
parameter_block_data	<参数块地址，参数块数据>，需要注意的是这里保存的参数块数据是原始参数块数据的一个拷贝，不再变化，用于记录这些参数块变量在marg时的状态
keep_block_size	<保留下来的参数块地址，参数块的globalsize>
keep_block_idx	<保留下来的参数块地址，参数块的索引>，保留下来的参数块是xb

成员函数信息：

成员函数	描述
preMarginalize	得到每次IMU和视觉观测对应的参数块，雅克比矩阵，残差值
marginalize	开启多线程构建信息矩阵H和b ，同时从H,b中恢复出线性化雅克比和残差

void marginalize()

    int pos = 0;    //pos表示所有的被marg掉的参数块以及它们的相连接参数块的localsize之和
    for (auto &it : parameter_block_idx)
    {
        it.second = pos;
        pos += localSize(parameter_block_size[it.first]);
    }

    m = pos;       

    for (const auto &it : parameter_block_size)
    {
        if (parameter_block_idx.find(it.first) == parameter_block_idx.end())
        {
            //将被marg掉参数的相连接参数块添加道parameter_block_idx中
            parameter_block_idx[it.first] = pos;
            pos += localSize(it.second);
        }
    }

    n = pos - m;

这里对参数块变量进行排序，待marg的参数块变量放在前面，其他参数块变量放在后面，并将每个参数块的对应的下标放在parameter_block_idx中。
pos = m + n

    TicToc t_thread_summing;
    pthread_t tids[NUM_THREADS];
    //携带每个线程的输入输出信息
    ThreadsStruct threadsstruct[NUM_THREADS];
    int i = 0;
    //将先验约束因子平均分配到线程中
    for (auto it : factors)
    {
        threadsstruct[i].sub_factors.push_back(it);
        i++;
        i = i % NUM_THREADS;
    }
    for (int i = 0; i < NUM_THREADS; i++)
    {
        TicToc zero_matrix;
        threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);
        threadsstruct[i].b = Eigen::VectorXd::Zero(pos);
        threadsstruct[i].parameter_block_size = parameter_block_size;
        threadsstruct[i].parameter_block_idx = parameter_block_idx;
        int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));
        if (ret != 0)
        {
            ROS_WARN("pthread_create error");
            ROS_BREAK();
        }
    }
    //将每个线程构建的A和b加起来
    for( int i = NUM_THREADS - 1; i >= 0; i--)  
    {
        pthread_join( tids[i], NULL );  //阻塞等待线程完成
        A += threadsstruct[i].A;
        b += threadsstruct[i].b;
    }

这段代码开启多线程来构建信息矩阵A和残差b。将所有的先验约束因子平均分配到NUM_THREADS个线程中，每个线程分别构建一个A和b。

void* ThreadsConstructA(void* threadsstruct)
{
    ThreadsStruct* p = ((ThreadsStruct*)threadsstruct);
    for (auto it : p->sub_factors)
    {
        for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
        {
            int idx_i = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];
            int size_i = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])];
            if (size_i == 7)
                size_i = 6;
            Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);//对于pose来说，是7维的,最后一维为0，这里取左边6维
            for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
            {
                int idx_j = p->parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
                int size_j = p->parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])];
                if (size_j == 7)
                    size_j = 6;
                Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);
                if (i == j)
                    p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                else
                {
                    p->A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                    p->A.block(idx_j, idx_i, size_j, size_i) = p->A.block(idx_i, idx_j, size_i, size_j).transpose();
                }
            }
            p->b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;
        }
    }
    return threadsstruct;
}

这部分代码是用来实现构建A和b的。

    Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);


    //ROS_ASSERT_MSG(saes.eigenvalues().minCoeff() >= -1e-4, "min eigenvalue %f", saes.eigenvalues().minCoeff());

    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
    //printf("error1: %f\n", (Amm * Amm_inv - Eigen::MatrixXd::Identity(m, m)).sum());

    Eigen::VectorXd bmm = b.segment(0, m);
    Eigen::MatrixXd Amr = A.block(0, m, m, n);
    Eigen::MatrixXd Arm = A.block(m, 0, n, m);
    Eigen::MatrixXd Arr = A.block(m, m, n, n);
    Eigen::VectorXd brr = b.segment(m, n);
    A = Arr - Arm * Amm_inv * Amr;
    b = brr - Arm * Amm_inv * bmm;

上面这段代码边缘化掉xm变量，保留xb变量，利用的方法是舒尔补。



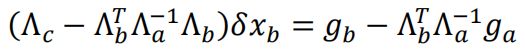
代码中求Amm的逆矩阵时，为了保证数值稳定性，做了Amm=1/2*(Amm+Amm^T)的运算，Amm本身是一个对称矩阵，所以等式成立。接着对Amm进行了特征值分解,再求逆，更加的快速。

    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
    Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
    Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));

    Eigen::VectorXd S_sqrt = S.cwiseSqrt();
    Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();

    linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
    linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;

上面这段代码是从A和b中恢复出雅克比矩阵和残差。


class MarginalizationFactor

class MarginalizationFactor : public ceres::CostFunction
{
  public:
    MarginalizationFactor(MarginalizationInfo* _marginalization_info);
    virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;

    MarginalizationInfo* marginalization_info;
};

类描述：该类是优化时表示上一步边缘化后保留下来的先验信息代价因子，变量marginalization_info保存了类似约束测量信息。

bool MarginalizationFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
    //printf("internal addr,%d, %d\n", (int)parameter_block_sizes().size(), num_residuals());
    //for (int i = 0; i < static_cast(keep_block_size.size()); i++)
    //{
    //    //printf("unsigned %x\n", reinterpret_cast(parameters[i]));
    //    //printf("signed %x\n", reinterpret_cast(parameters[i]));
    //printf("jacobian %x\n", reinterpret_cast(jacobians));
    //printf("residual %x\n", reinterpret_cast(residuals));
    //}
    int n = marginalization_info->n;
    int m = marginalization_info->m;
    Eigen::VectorXd dx(n);
    for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
    {
        int size = marginalization_info->keep_block_size[i];
        int idx = marginalization_info->keep_block_idx[i] - m;
        Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size);
        //x0表示marg时参数块变量的值(即xb)
        Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size);
        if (size != 7)
            dx.segment(idx, size) = x - x0;
        else
        {
            dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();
            dx.segment<3>(idx + 3) = 2.0 * Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
            if (!((Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).w() >= 0))
            {
                dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
            }
        }
    }
    Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;
    if (jacobians)
    {

        for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
        {
            if (jacobians[i])
            {
                int size = marginalization_info->keep_block_size[i], local_size = marginalization_info->localSize(size);
                int idx = marginalization_info->keep_block_idx[i] - m;
                Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);
                jacobian.setZero();
                jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);
            }
        }
    }
    return true;
}

上面这段代码是在优化过程中，对先验约束项的更新，主要是对先验残差的更新，雅克比不再发生变化。
代码中的x0表示marg xm状态时xb变量的值。
优化过程中先验项的雅克比保持不变，但是残差需要变化，其变化公式推导如下：

参考资源：
[1] Decopuled, Consistent Node Removal and Edge Sparsification for Graph-based SLAM
[2] A Tutorial on Graph-Based SLAM
[3] 崔华坤，VINS论文推导及代码解析
[4] 深蓝学院VIO课程第一期