[机器学习]朴素贝叶斯原理及python源码

朴素贝叶斯的思想

思想很简单，就是根据某些个先验概率计算Y变量属于某个类别的后验概率，请看下图细细道来：

假如，上表中的信息反映的是某P2P企业判断其客户是否会流失(churn)，而影响到该变量的因素包含年龄、性别、收入、教育水平、消费频次、支出。那根据这样一个信息，我该如何理解朴素贝叶斯的思想呢？再来看一下朴素贝叶斯公式：

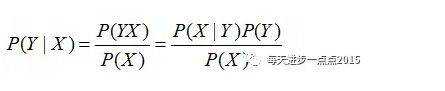
从公式中可知，如果要计算X条件下Y发生的概率,只需要计算出后面等式的三个部分，X事件的概率（P(X)），是X的先验概率、Y属于某类的概率（P(Y)），是Y的先验概率、以及已知Y的某个分类下，事件X的概率（P(X|Y)），是后验概率。从上表中，是可以计算这三种概率值的。即：
P(x) 指在所有客户集中，某位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率；

P(Y) 指流失与不流失在所有客户集中的比例；

P(X|Y) 指在已知流失的情况下，一位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率。

如果要确定某个样本归属于哪一类，则需要计算出归属不同类的概率，再从中挑选出最大的概率。

我们把上面的贝叶斯公式写出这样，也许你能更好的理解:

而这个公式告诉我们，需要计算最大的后验概率，只需要计算出分子的最大值即可，而不同水平的概率P©非常容易获得，故难点就在于P(X|C)的概率计算。而问题的解决，正是聪明之处，即贝叶斯假设变量X间是条件独立的，故而P(X|C)的概率就可以计算为：

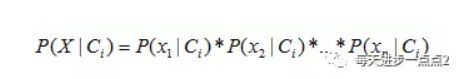
也许，这个公式你不明白，我们举个例子（上表的数据）说明就很容易懂了。

对于离散情况：

假设已知某个客户流失的情况下，其性别为女，教育水平为本科的概率：

上式结果中的分母4为数据集中流失有4条观测，分子2分别是流失的前提下，女性2名，本科2名。

假设已知某个客户未流失的情况下，其性别为女，教育水平为本科的概率:

上式结果中的分母3为数据集中未流失的观测数，分子2分别是未流失的前提下，女性2名，本科2名。
从而P(C|X)公式中的分子结果为：

对于连续变量的情况就稍微复杂一点，并非计算频率这么简单，而是假设该连续变量服从正态分布（即使很多数据并不满足这个条件），先来看一下正态分布的密度函数:

要计算连续变量中某个数值(一条数据里的每一特征的值)的概率，只需要已知该变量的均值和标准差，再将该数值带入到上面的公式即可。

接下来附上朴素贝叶斯的源码(用高斯分布拟合p(x|y)):

import numpy as np 
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import normalize
from sklearn.metrics import accuracy_score

class NaiveBayes:
    def fit(self, x, y):
        self.x = x
        self.y = y
        self.classes = np.unique(y)
        print(self.classes)
        self.parameters = {}
        for i , c in enumerate(self.classes):
            #计算属于同一类别的均值,方差和各类别的先验概率p(y).
            X_index_c  = x[np.where(y == c)]
            X_index_c_mean = np.mean(X_index_c, axis=0, keepdims=True)
            X_index_c_var = np.var(X_index_c, axis=0, keepdims=True)
            parameters = {'mean':X_index_c_mean,'var':X_index_c_var,'prior':X_index_c.shape[0]/ x.shape[0]}
            self.parameters['class' + str(c)] = parameters  #字典嵌套
            print(X_index_c.shape[0])
        
    def _pdf(self, x, classes):
        #用高斯分布拟合p(x|y),也就是后验概率.并且按行每个特征的p(x|y)累乘,取log成为累加.
        eps = 1e-4  #防止分母为0
        mean = self.parameters['class' + str(classes)]['mean']
        var  = self.parameters['class' + str(classes)]['var']
        fenzi = np.exp(-(x - mean) ** 2 / (2 * (var) ** 2 + eps))
        fenmu = (2 * np.pi) ** 0.5 * var + eps
        result = np.sum(np.log(fenzi / fenmu), axis=1, keepdims=True)
        #print(result.T.shape)
        return result.T #(1, 719)
       
        
    def _predict(self, x):
        # 计算每个种类的p(y)p(x|y)
        output = []
        for y in range(self.classes.shape[0]):
            prior = np.log(self.parameters['class' + str(y)]['prior'])
            posterior = self._pdf(x, y)
            prediction = prior + posterior
            output.append(prediction)
        return output
        
    def predict(self, x):
        #argmax(p(y)p(x|y))就是最终的结果
        output = self._predict(x)
        output = np.reshape(output, (self.classes.shape[0], x.shape[0]))
        prediction = np.argmax(output, axis=0)
        return prediction
        
if __name__=='__main__':
    data = datasets.load_digits()
    x = normalize(data.data)
    y = data.target
    x_train,x_test,y_train,y_test = train_test_split(x, y, test_size = 0.4)
    print('x_tarin', x_train.shape)
    clf = NaiveBayes()
    clf.fit(x_train, y_train)
    y_pred = clf.predict(x_test)
    accuracy = accuracy_score(y_test, y_pred)
    print('Accuracy:', accuracy)

结果如下: