LDA求解：Gibbs采样算法

本文是LDA主题模型的第二篇，读这一篇之前建议先读文本主题模型之LDA(一) LDA基础，同时由于使用了基于MCMC的Gibbs采样算法，如果你对MCMC和Gibbs采样不熟悉，建议阅读之前写的MCMC系列MCMC(四)Gibbs采样。

 

1. Gibbs采样算法求解LDA的思路

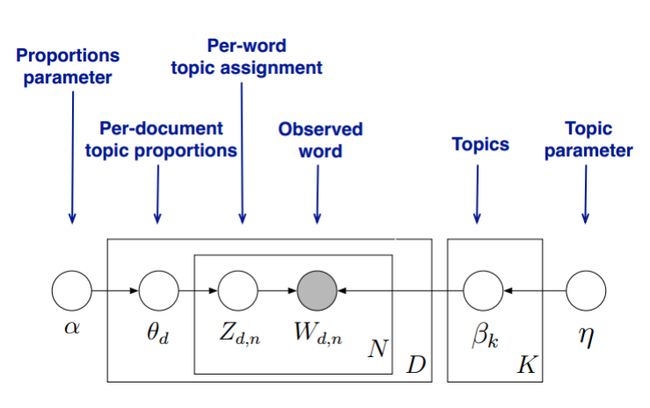
　　　　首先，回顾LDA的模型图如下：

　　　　在Gibbs采样算法求解LDA的方法中，我们的α,ηα,η是已知的先验输入,我们的目标是得到各个zdn,wknzdn,wkn对应的整体z⃗ ,w⃗ z→,w→的概率分布，即文档主题的分布和主题词的分布。由于我们是采用Gibbs采样法，则对于要求的目标分布，我们需要得到对应分布各个特征维度的条件概率分布。

　　　　具体到我们的问题，我们的所有文档联合起来形成的词向量w⃗ w→是已知的数据，不知道的是语料库主题z⃗ z→的分布。假如我们可以先求出w,zw,z的联合分布p(w⃗ ,z⃗ )p(w→,z→)，进而可以求出某一个词wiwi对应主题特征zizi的条件概率分布p(zi=k|w⃗ ,z⃗ ¬i)p(zi=k|w→,z→¬i)。其中，z⃗ ¬iz→¬i代表去掉下标为ii的词后的主题分布。有了条件概率分布p(zi=k|w⃗ ,z⃗ ¬i)p(zi=k|w→,z→¬i)，我们就可以进行Gibbs采样，最终在Gibbs采样收敛后得到第ii个词的主题。

　　　　如果我们通过采样得到了所有词的主题,那么通过统计所有词的主题计数，就可以得到各个主题的词分布。接着统计各个文档对应词的主题计数，就可以得到各个文档的主题分布。

　　　　以上就是Gibbs采样算法求解LDA的思路。

2. 主题和词的联合分布与条件分布的求解

　　　　从上一节可以发现，要使用Gibbs采样求解LDA，关键是得到条件概率p(zi=k|w⃗ ,z⃗ ¬i)p(zi=k|w→,z→¬i)的表达式。那么这一节我们的目标就是求出这个表达式供Gibbs采样使用。

　　　　首先我们简化下Dirichlet分布的表达式,其中△(α)△(α)是归一化参数：

Dirichlet(p⃗ |α⃗ )=Γ(∑k=1Kαk)∏Kk=1Γ(αk)∏k=1Kpαk−1k=1△(α⃗ )∏k=1Kpαk−1kDirichlet(p→|α→)=Γ(∑k=1Kαk)∏k=1KΓ(αk)∏k=1Kpkαk−1=1△(α→)∏k=1Kpkαk−1

 

　　　　现在我们先计算下第d个文档的主题的条件分布p(z⃗ d|α)p(z→d|α)，在上一篇中我们讲到α→θd→z⃗ dα→θd→z→d组成了Dirichlet-multi共轭,利用这组分布，计算p(z⃗ d|α⃗ )p(z→d|α→)如下：

p(z⃗ d|α⃗ )=∫p(z⃗ d|θ⃗ d)p(θd|α⃗ )dθ⃗ d=∫∏k=1Kpn(k)dkDirichlet(α⃗ )dθ⃗ d=∫∏k=1Kpn(k)dk1△(α⃗ )∏k=1Kpαk−1kdθ⃗ d=1△(α⃗ )∫∏k=1Kpn(k)d+αk−1kdθ⃗ d=△(n⃗ d+α⃗ )△(α⃗ )(1)(2)(3)(4)(5)(1)p(z→d|α→)=∫p(z→d|θ→d)p(θd|α→)dθ→d(2)=∫∏k=1Kpknd(k)Dirichlet(α→)dθ→d(3)=∫∏k=1Kpknd(k)1△(α→)∏k=1Kpkαk−1dθ→d(4)=1△(α→)∫∏k=1Kpknd(k)+αk−1dθ→d(5)=△(n→d+α→)△(α→)

 

　　　　其中，在第d个文档中，第k个主题的词的个数表示为：n(k)dnd(k), 对应的多项分布的计数可以表示为

n⃗ d=(n(1)d,n(2)d,...n(K)d)n→d=(nd(1),nd(2),...nd(K))

 

　　　　有了单一一个文档的主题条件分布，则可以得到所有文档的主题条件分布为：

p(z⃗ |α⃗ )=∏d=1Mp(z⃗ d|α⃗ )=∏d=1M△(n⃗ d+α⃗ )△(α⃗ )p(z→|α→)=∏d=1Mp(z→d|α→)=∏d=1M△(n→d+α→)△(α→)

 

　　　　同样的方法，可以得到，第k个主题对应的词的条件分布p(w⃗ |z⃗ ,η⃗ )p(w→|z→,η→)为：

p(w⃗ |z⃗ ,η⃗ )=∏k=1Kp(w⃗ k|z⃗ ,η⃗ )=∏k=1K△(n⃗ k+η⃗ )△(η⃗ )p(w→|z→,η→)=∏k=1Kp(w→k|z→,η→)=∏k=1K△(n→k+η→)△(η→)

 

　　　　其中，第k个主题中，第v个词的个数表示为：n(v)knk(v), 对应的多项分布的计数可以表示为

n⃗ k=(n(1)k,n(2)k,...n(V)k)n→k=(nk(1),nk(2),...nk(V))

 

　　　　最终我们得到主题和词的联合分布p(w⃗ ,z⃗ |α⃗ ,η⃗ )p(w→,z→|α→,η→)如下：

p(w⃗ ,z⃗ )∝p(w⃗ ,z⃗ |α⃗ ,η⃗ )=p(z⃗ |α⃗ )p(w⃗ |z⃗ ,η⃗ )=∏d=1M△(n⃗ d+α⃗ )△(α⃗ )∏k=1K△(n⃗ k+η⃗ )△(η⃗ )p(w→,z→)∝p(w→,z→|α→,η→)=p(z→|α→)p(w→|z→,η→)=∏d=1M△(n→d+α→)△(α→)∏k=1K△(n→k+η→)△(η→)

 

　　　　有了联合分布，现在我们就可以求Gibbs采样需要的条件分布p(zi=k|w⃗ ,z⃗ ¬i)p(zi=k|w→,z→¬i)了。需要注意的是这里的i是一个二维下标，对应第d篇文档的第n个词。

　　　　对于下标ii,由于它对应的词wiwi是可以观察到的，因此我们有：

p(zi=k|w⃗ ,z⃗ ¬i)∝p(zi=k,wi=t|w⃗ ¬i,z⃗ ¬i)p(zi=k|w→,z→¬i)∝p(zi=k,wi=t|w→¬i,z→¬i)

 

　　　　对于zi=k,wi=tzi=k,wi=t,它只涉及到第d篇文档和第k个主题两个Dirichlet-multi共轭，即：

α⃗ →θ⃗ d→z⃗ dα→→θ→d→z→d

η⃗ →β⃗ k→w⃗ (k)η→→β→k→w→(k)

 

　　　　其余的M+K−2M+K−2个Dirichlet-multi共轭和它们这两个共轭是独立的。如果我们在语料库中去掉zi,wizi,wi,并不会改变之前的M+KM+K个Dirichlet-multi共轭结构，只是向量的某些位置的计数会减少，因此对于θ⃗ d,β⃗ kθ→d,β→k,对应的后验分布为：

p(θ⃗ d|w⃗ ¬i,z⃗ ¬i)=Dirichlet(θ⃗ d|n⃗ d,¬i+α⃗ )p(θ→d|w→¬i,z→¬i)=Dirichlet(θ→d|n→d,¬i+α→)

p(β⃗ k|w⃗ ¬i,z⃗ ¬i)=Dirichlet(β⃗ k|n⃗ k,¬i+η⃗ )p(β→k|w→¬i,z→¬i)=Dirichlet(β→k|n→k,¬i+η→)

 

　　　　现在开始计算Gibbs采样需要的条件概率：

p(zi=k|w⃗ ,z⃗ ¬i)∝p(zi=k,wi=t|w⃗ ¬i,z⃗ ¬i)=∫p(zi=k,wi=t,θ⃗ d,β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k,θ⃗ d|w⃗ ¬i,z⃗ ¬i)p(wi=t,β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k|θ⃗ d)p(θ⃗ d|w⃗ ¬i,z⃗ ¬i)p(wi=t|β⃗ k)p(β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k|θ⃗ d)Dirichlet(θ⃗ d|n⃗ d,¬i+α⃗ )dθ⃗ d∗∫p(wi=t|β⃗ k)Dirichlet(β⃗ k|n⃗ k,¬i+η⃗ )dβ⃗ k=∫θdkDirichlet(θ⃗ d|n⃗ d,¬i+α⃗ )dθ⃗ d∫βktDirichlet(β⃗ k|n⃗ k,¬i+η⃗ )dβ⃗ k=EDirichlet(θd)(θdk)EDirichlet(βk)(βkt)(6)(7)(8)(9)(10)(11)(12)(13)(6)p(zi=k|w→,z→¬i)∝p(zi=k,wi=t|w→¬i,z→¬i)(7)=∫p(zi=k,wi=t,θ→d,β→k|w→¬i,z→¬i)dθ→ddβ→k(8)=∫p(zi=k,θ→d|w→¬i,z→¬i)p(wi=t,β→k|w→¬i,z→¬i)dθ→ddβ→k(9)=∫p(zi=k|θ→d)p(θ→d|w→¬i,z→¬i)p(wi=t|β→k)p(β→k|w→¬i,z→¬i)dθ→ddβ→k(10)=∫p(zi=k|θ→d)Dirichlet(θ→d|n→d,¬i+α→)dθ→d(11)∗∫p(wi=t|β→k)Dirichlet(β→k|n→k,¬i+η→)dβ→k(12)=∫θdkDirichlet(θ→d|n→d,¬i+α→)dθ→d∫βktDirichlet(β→k|n→k,¬i+η→)dβ→k(13)=EDirichlet(θd)(θdk)EDirichlet(βk)(βkt)

 

　　　　在上一篇LDA基础里我们讲到了Dirichlet分布的期望公式，因此我们有：

EDirichlet(θd)(θdk)=nkd,¬i+αk∑s=1Knsd,¬i+αsEDirichlet(θd)(θdk)=nd,¬ik+αk∑s=1Knd,¬is+αs

EDirichlet(βk)(βkt)=ntk,¬i+ηt∑f=1Vnfk,¬i+ηfEDirichlet(βk)(βkt)=nk,¬it+ηt∑f=1Vnk,¬if+ηf

 

　　　　最终我们得到每个词对应主题的Gibbs采样的条件概率公式为：

p(zi=k|w⃗ ,z⃗ ¬i)=nkd,¬i+αk∑s=1Knsd,¬i+αsntk,¬i+ηt∑f=1Vnfk,¬i+ηfp(zi=k|w→,z→¬i)=nd,¬ik+αk∑s=1Knd,¬is+αsnk,¬it+ηt∑f=1Vnk,¬if+ηf

 

　　　　有了这个公式，我们就可以用Gibbs采样去采样所有词的主题，当Gibbs采样收敛后，即得到所有词的采样主题。

　　　　利用所有采样得到的词和主题的对应关系，我们就可以得到每个文档词主题的分布θdθd和每个主题中所有词的分布βkβk。

3. LDA Gibbs采样算法流程总结

　　　　现在我们总结下LDA Gibbs采样算法流程。首先是训练流程：

　　　　1） 选择合适的主题数KK, 选择合适的超参数向量α⃗ ,η⃗ α→,η→

　　　　2） 对应语料库中每一篇文档的每一个词，随机的赋予一个主题编号zz

　　　　3)  重新扫描语料库，对于每一个词，利用Gibbs采样公式更新它的topic编号，并更新语料库中该词的编号。

　　　　4） 重复第2步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。

　　　　5） 统计语料库中的各个文档各个词的主题，得到文档主题分布θdθd，统计语料库中各个主题词的分布，得到LDA的主题与词的分布βkβk。

 

　　　　下面我们再来看看当新文档出现时，如何统计该文档的主题。此时我们的模型已定，也就是LDA的各个主题的词分布βkβk已经确定，我们需要得到的是该文档的主题分布。因此在Gibbs采样时，我们的EDirichlet(βk)(βkt)EDirichlet(βk)(βkt)已经固定，只需要对前半部分EDirichlet(θd)(θdk)EDirichlet(θd)(θdk)进行采样计算即可。

　　　　现在我们总结下LDA Gibbs采样算法的预测流程：

　　　　1） 对应当前文档的每一个词，随机的赋予一个主题编号zz

　　　　2)  重新扫描当前文档，对于每一个词，利用Gibbs采样公式更新它的topic编号。

　　　　3） 重复第2步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。

　　　　4） 统计文档中各个词的主题，得到该文档主题分布。

 

4. LDA Gibbs采样算法小结 　　　

　　　　使用Gibbs采样算法训练LDA模型，我们需要先确定三个超参数K,α⃗ ,η⃗ K,α→,η→。其中选择一个合适的KK尤其关键,这个值一般和我们解决问题的目的有关。如果只是简单的语义区分，则较小的KK即可，如果是复杂的语义区分，则KK需要较大，而且还需要足够的语料。

　　　　由于Gibbs采样可以很容易的并行化，因此也可以很方便的使用大数据平台来分布式的训练海量文档的LDA模型。以上就是LDA Gibbs采样算法。

　　　　后面我们会介绍用变分推断EM算法来求解LDA主题模型，这个方法是scikit-learn和spark MLlib都使用的LDA求解方法。