【第6节】零基础新手的Python入门实战宝典(五·番外实战篇) —— 利用Python秒解方程
如果你之前看过其他教程,但是发现云里雾里复杂的让你头晕眼花的话,没错,看这里,本系列Python教程专为啥都不会的新手用户打造,放宽心,大胆看,我就是说说书,你就当听听故事,轻松愉快走进编程的大门,“程序设计”不再神秘也不再遥不可及。只要你会最基本的电脑操作(装装软件打打字),读过那么几天书,汉字都认识,英文会那么一点点就够了,包学包会!Let’s go!
【本节目录】
文章目录
- 1. 创建项目
- 2. 详细讲解如何自动“解一元二次方程”
- 3. 小结
这一节可以看做是上一节的实战篇,学习编程什么最重要,当然是动手啦!因为学习编程的最终目的,还是要能够将学习到的编程技术用于提高自己的工作和生活效率啊!
学习了前面的内功心法(“函数”或“功能”),也学习了最简单最基础的“数据类型”(数字和字符串),其实我们就可以做一些事情了。本节我们来亲手实践一下!
还记得前面用Python命令计算机来解方程的神奇事件吗?不管系数多么复杂,利用Python来让计算机进行计算,瞬间就能计算出 x x x的值。这是怎么实现的呢?有了前面的心法和基础知识,就很容易掌握了,我来帮大家一步一步拆解这套解方程的“武功”流程。
1. 创建项目
用编程语言控制计算机进行操作的时候,需要我们先把要做的事情都写下来,然后把这个任务要求扔给计算机,让计算机自己来执行,最后把执行的结果告诉你。所以,我们要做的第一步是什么呢?哈哈,是准备一张纸或者一个本子,用来写任务要求和计划。在现实中,可能你有几件或者几十件需要计算机来做的事情,全都混乱地不加分类标签全都一股脑写在同一个本子上肯定不行啊,所以就需要准备好几个本子,每个本子只用来记录一项工作的内容。现实中我们所使用的“本子”,也就是编程中的“项目”。每当我们有一项新的工作,我们觉得需要一个新的“本子”来记录的时候,对应到计算机编程的话,我们就创建一个新的“项目”。
使用PyCharm创建项目的步骤如下:
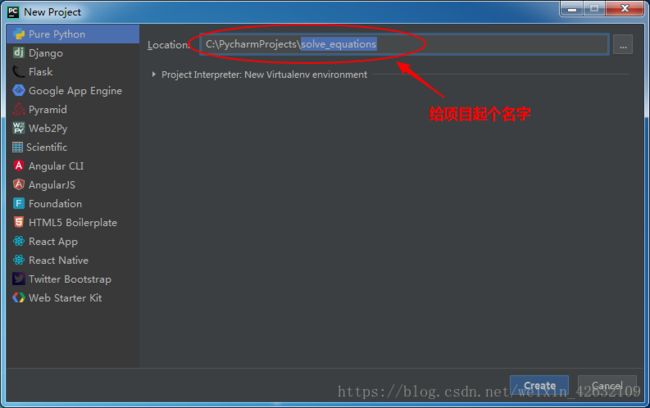
①打开PyCharm点“Create New Project”(创建新项目)
②设置项目的相关信息,然后点右下角的“Create"来创建项目
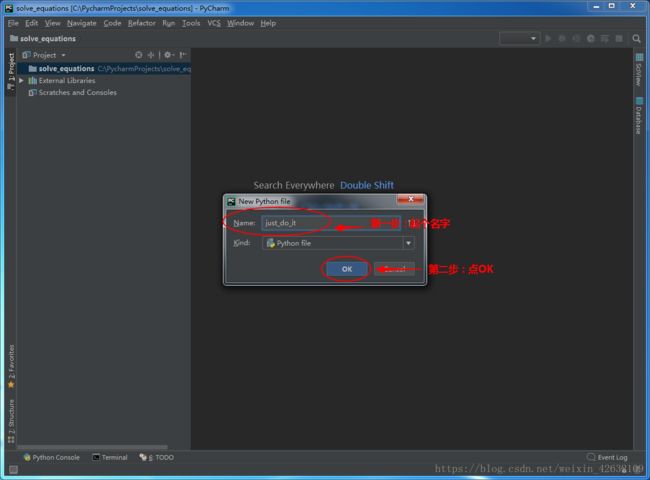
③新建一个文件(刚刚建立的“项目”与“文件”的关系,可以类比成“本子”与本子中的“纸”的关系。)
④给文件起个名字,这个名字根据自己喜好起名即可(我起的名字是just_do_it)
这样我们就完成了编写程序的准备工作,界面是下面这个样子滴:
后面我们要做的,就是在右边中央的这一大块编辑区进行程序的编写了。
2. 详细讲解如何自动“解一元二次方程”
学过如何解一元二次方程的我们肯定都知道,有个很神奇的东西就是解一元二次方程的求根公式: x 1 , 2 = − b ± b 2 − 4 a c 2 a x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} x1,2=2a−b±b2−4ac 。只要把三个系数a、b、c代入求根公式,就能直接求出一元二次方程的两个解!
对于不同的一元二次方程,a、b、c三个系数的组合方式各不相同,对于每个新的一元二次方程,我们都得在演草纸上细心计算一番,还得特别小心不能算错,然后才能得出这个方程的两个解。但是,当我们有了计算机,有了程序,有了Python,这一切就不一样了,我们完全可以让计算机自动来帮我们完成计算,而且计算地又快又准!
下面就是解一元二次方程的Python程序代码,然后我来一步一步手把手告诉你,Python是怎么做到的!(插播一个小知识,在每一行中,如果看到一个#号,那么这个#后面的内容就是对这一行代码的解释说明,下面的程序里也会用这种方式进行一些解释。)
a = 1 # 系数a的值为1
b = -5 # 系数b的值为-5
c = 6 # 系数c的值为6
m = (b ** 2 - 4 * a * c) ** (1 / 2)
x1 = (-b + m) / (2 * a)
x2 = (-b - m) / (2 * a)
print("第一个解为:" + str(x1))
print("第二个解为:" + str(x2))
讲解之前,我们先来看下效果:
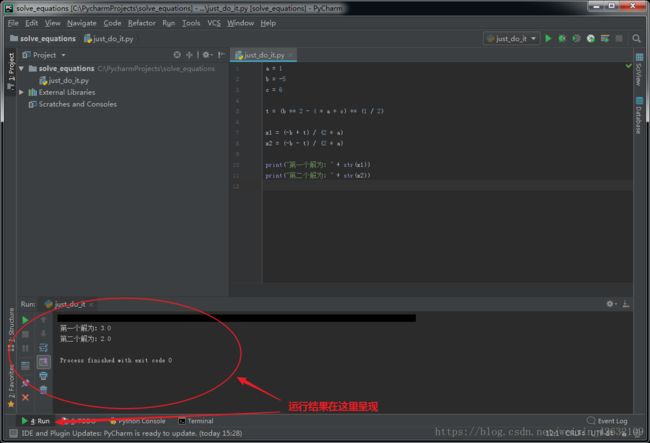
①把上面的代码复制粘贴到编辑区,然后运行
②结果如下图所示
怎么样?是不是很厉害!自己试试修改a、b、c三个系数的值,只要符合一元二次方程的系数要求,计算机都能瞬间计算出方程的两个解!接下来,我们就来讲解下Python是怎么做到的!
上面代码的前3行,通过#后面的解释,大家应该明白是什么意思了。比如说a = 1就是给变量a赋值为数字1,也就是说,在程序里一提到变量a,大家就知道是数字1。b和c也是同样的原理。
接下来我们来看第5行m = (b ** 2 - 4 * a * c) ** (1 / 2),这一行看起来就有些复杂了吧?看我的分解动作!
还是类似于上一节,Python里有一些表达方法跟人类语言不太一样,这里还是用表格的方式给大家呈现一下,这样的话对应关系会更加清晰:
| 数学中的符号 | Python中的符号 | 说明 |
|---|---|---|
| + + + | + |
“加号”相同 |
| − - − | - |
“减号”相同 |
| × × × | * |
“乘号”对应*号 |
| ÷ ÷ ÷ | / |
“除号”对应/号 |
| 幂指数 | ** |
幂指数公式: y = a x y=a^x y=ax |
| 数学中的表达 | Python中的写法 |
|---|---|
| y = x + a y=x+a y=x+a | y = x + a |
| y = x − a y=x-a y=x−a | y = x - a |
| y = x × a y=x×a y=x×a | y = x * a |
| y = x ÷ a y=x÷a y=x÷a | y = x / a |
| y = a x y=a^x y=ax | y = a ** x |
然后我们再来重新审视一下这行代码:
m = (b ** 2 - 4 * a * c) ** (1 / 2)
根据上面的对应关系,有没有发现,其实这里的m实际上就是求根公式里的 b 2 − 4 a c \sqrt{b^2-4ac} b2−4ac 这一部分!第一个括号里的b ** 2是 b 2 b^2 b2,4 * a * c是 4 a c 4ac 4ac,开根号实际上也就是二分之一次方。所以写成一行之后,就是m = (b ** 2 - 4 * a * c) ** (1 / 2)。通过这一行代码,我们就能求出m的值,然后我们的求根公式就进一步简化成了 x 1 , 2 = − b ± m 2 a x_{1,2}=\frac{-b\pm m}{2a} x1,2=2a−b±m 。
然后第7行代码x1 = (-b + m) / (2 * a)和第8行代码x2 = (-b - m) / (2 * a)就可以分别求出来两个解了。这两个解对应的变量一个是x1,另一个是x2。
到这里,我们实际上已经利用Python语言命令计算机完成了自动求解一元二次方程的全部过程了!但计算完之后,结果只有计算机自己知道,所以我们还需要利用第10和第11这两行代码让计算机把结果呈现在屏幕上,这样才能让我们看得到。
还记得之前的第(四)节里的内功心法吧?关于“方法”或“函数”那里。解读第10和第11就需要用到这个知识了。在第(四)节中也提到过print()这个函数,我们现在要做的就是利用这个函数把计算结果呈现在屏幕上。第10行和第11行这两行代码就完美地完成了这个要求。(至于str(x1)和str(x2)是干嘛用的,这里就卖个关子先不说,后面写到相关章节的时候会进行详细讲解。特别特别想赶紧知道的同学,一定要自己动手去找资料哟,学习编程说到底还是自己动手最重要!)
3. 小结
这一节的内容是我们真正意义上的动手实践了,是不是很有趣很厉害?!再也不用一点儿一点儿去演算了,真正的解放双手啦!其实Python能做的远不止于此,这种小事儿实际上都用不到计算机百万分之一的实力!所以,现在是不是更有动力去学好编程了呢?那我们下节不见不散哟!_