随机采样方法代码实现-python

1. 均匀分布，使用线性同余器

from datetime import datetime
from math import sqrt, cos, pi, log
import matplotlib.pyplot as plt
import numpy as np


def uniform_gen(seed, a=0, b=1):
    _A = 214013
    _C = 214013
    _M = 2 ** 32
    while True:
        seed = (_A * seed + _C) % _M
        res = a + (b - a) * seed / _M
        yield res


def random_uniform(num, seed=None):
    res = []
    if not seed:
        seed = datetime.now().second
    gen = uniform_gen(seed)
    if num == 1:
        return gen.__next__()
    for i in range(num):
        res.append(gen.__next__())
    return np.array(res)

def plot_hist(x, bin=150, path = None):
    plt.hist(x, bin)
    if path:
        plt.savefig(path)
    plt.show()


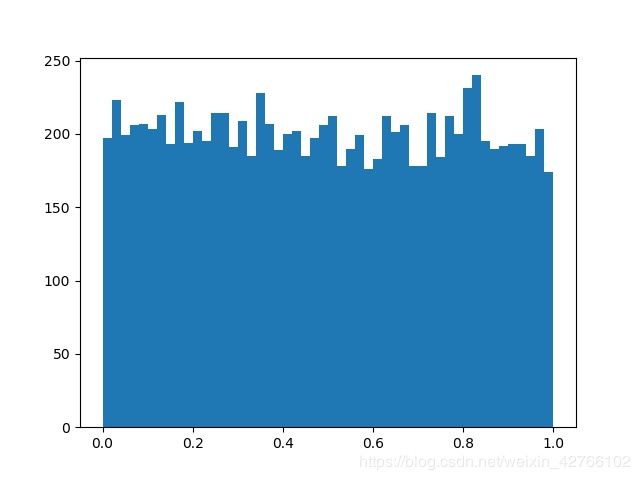
res = random_uniform(10000)
plot_hist(res, 50, 'uniform.jpg')

2. Box-Muller变换正态分布

def box_muller(num, loc=0., scale=1.):
    seed1 = datetime.now().second
    seed2 = datetime.now().minute
    gen1 = uniform_gen(seed1)
    gen2 = uniform_gen(seed2)
    res = []
    for i in range(num):
        u1 = gen1.__next__()
        u2 = gen2.__next__()
        u = sqrt(-2 * log(u1)) * cos(2 * pi * u2)
        u = (u + loc) * scale
        res.append(u)
    return np.array(res)


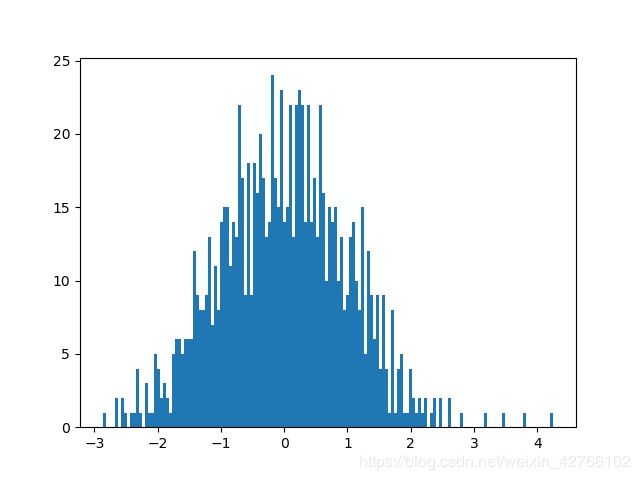
res = box_muller(1000)
plot_hist(res, path='box_nuller.jpg')

3. 接受-拒绝采样

目标是生成服从代码块中的p(x)密度函数分布的样本，用kq(x)密度函数覆盖住p(x)，使得p(x)<=kq(x)。具体原理参考随机采样方法整理与讲解（MCMC、Gibbs Sampling等）
不好的地方是很难找到合适的q分布，k的确定也麻烦。

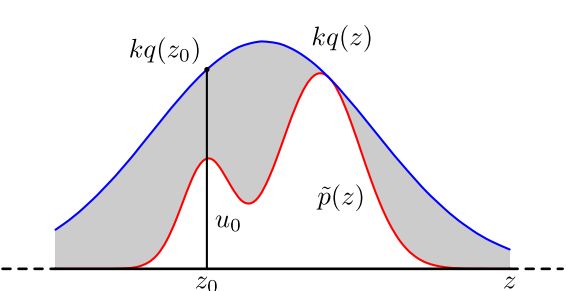
def p(x):
    return (0.3 * np.exp(-(x - 0.3) ** 2) + 0.7 * np.exp(-(x - 2.) ** 2 / 0.3)) / 1.2113


def q(x, loc=0, scale=1):
    return 1 / (np.sqrt(2 * np.pi) * scale) * np.exp(-0.5 * (x - loc) ** 2 / scale ** 2)


def reject_sampling(pdf, k, loc, scale, num=1000):
    normal_sampling = box_muller(num, loc=loc, scale=scale)
    origin_pdf = pdf(normal_sampling)
    cover_pdf = q(normal_sampling, loc, scale) * k
    u = random_uniform(num) * cover_pdf
    res = normal_sampling[origin_pdf > u]
    return res


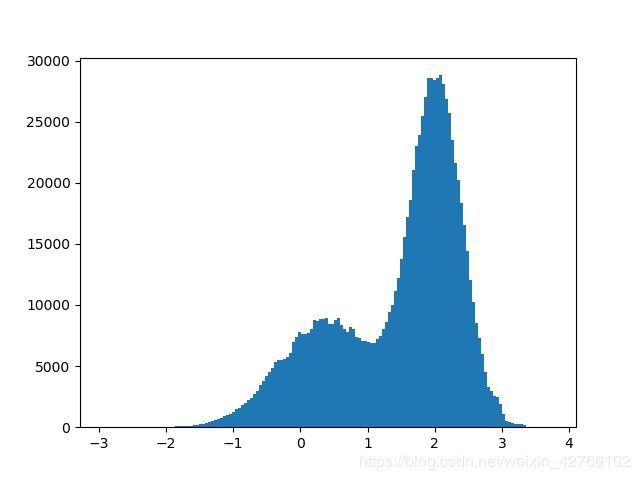
res = reject_sampling(p, 10, 1.4, 1.2, int(1e+7))

plot_hist(res)

4. MCMC采样变体-Metropolis-Hastings算法

MCMC采样是从马氏链的平稳分布原理出发，构造转移概率矩阵使得马氏链的平稳分布为恰好为你想要生成的抽样分布$p(x)$。Metropolis算法对MCMC改进的地方在于对接受率$\alpha (x_t,y)$做了改进，具体可参考LDA数学八卦。
代码中取$q(x|x_t)=q(x)$，$q(x)$为均匀分布,因此$\alpha =min\{\frac{p(y)}{p(x_t)},1\}$。另外一个值得注意的地方是$q(x)$的选取要根据你想生成的分布$p(x)$来改变，$q(x)$至少要覆盖住$p(x)$那些概率密度比较高的点。

def p(x):
    return 1 / (2 * np.pi) * np.exp(-x[0] ** 2 - x[1] ** 2)


def uniform_gen():
    # 计算定义域一个随机值
    return np.random.random() * 4 - 2


def metropolis(x0):
    x = (uniform_gen(), uniform_gen())
    u = np.random.uniform()
    alpha = min(1, p(x) / p(x0))
    if u < alpha:
        return x
    else:
        return x0


def gen_px(num):
    x = (uniform_gen(), uniform_gen())
    res = [x]
    for i in range(num):
        x = metropolis(x)
        res.append(x)
    return np.array(res)


def plt_scatter(x, path=None):
    x = np.array(x)
    plt.scatter(x[:, 0], x[:, 1])
    if path:
        plt.savefig(path)
    plt.show()


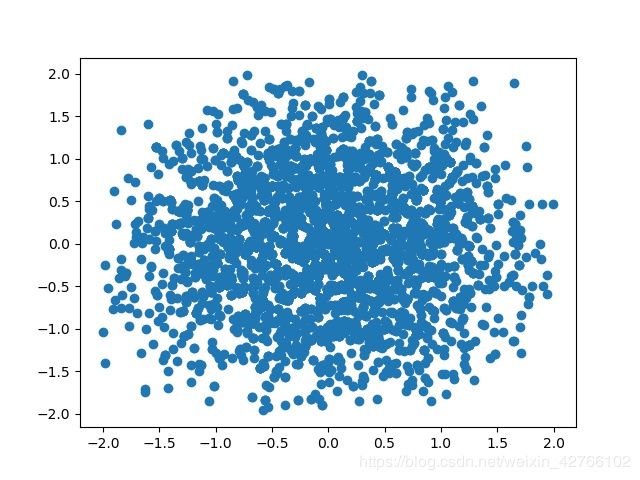
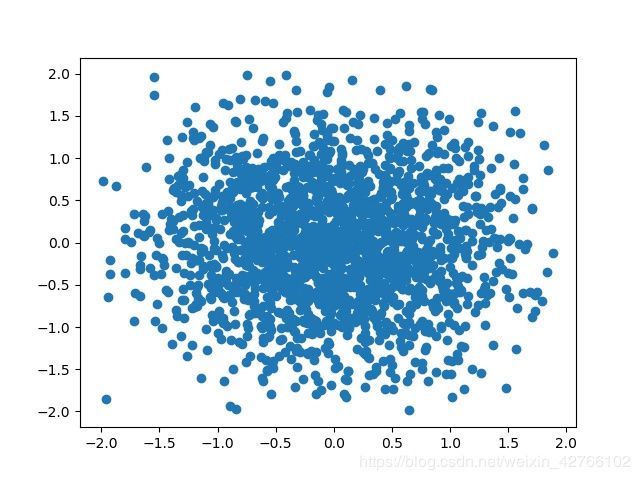
res = gen_px(5000)
plt_scatter(res, 'MCMC.jpg')

5. Gibbs抽样

即使对MCMC抽样的接受率$\alpha$进行改进，高维情况下Metropolis算法的效率还是有点低。所以闲着无聊的数学家们就在考虑能不能找到一个概率转移矩阵使得$\alpha =1$，然后就发现在单个维度进行概率转移的话就能满足这个条件。原理参考LDA数学八卦，代码参考采样方法（二）MCMC相关算法介绍及代码实现

def one_dim_transit(x, dim):
    candidates = []
    probs = []
    for i in range(10):
        tmp = x[:]
        tmp[dim] = uniform_gen()
        candidates.append(tmp[dim])
        probs.append(p(tmp))
    norm_probs = np.array(probs) / sum(probs)
    u = np.random.uniform()
    sum_probs = 0
    for i in range(10):
        sum_probs += norm_probs[i]
        if sum_probs >= u:
            return candidates[i]


def gibbs(x):
    dim = len(x)
    new = x[:]
    for i in range(dim):
        new[i] = one_dim_transit(new, i)
    return new


def gibbs_sampling(num=1000):
    x = [uniform_gen(), uniform_gen()]
    res = [x]
    for i in range(num):
        res.append(gibbs(x))
    return res
    
res = gibbs_sampling(2000)
plt_scatter(res, path='gibbs.jpg')

参考资料
LDA数学八卦
随机采样方法整理与讲解（MCMC、Gibbs Sampling等）
采样方法（二）MCMC相关算法介绍及代码实现