Python与Ansys apdl有限元系列一:平面2D桁架竖向集中载荷
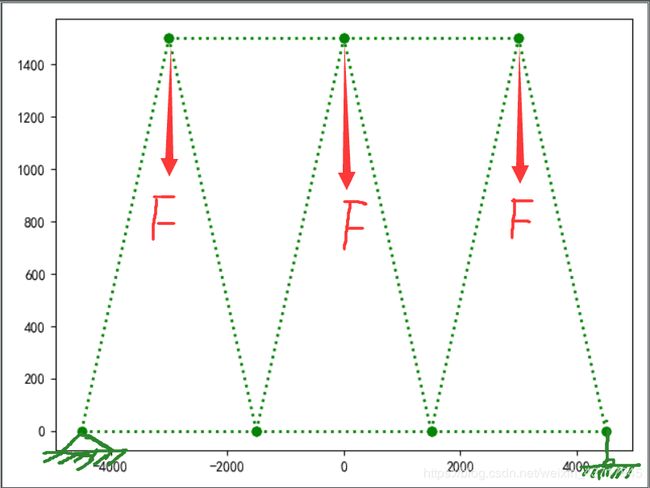
1. 二维静定桁架,结构各个参数如下
弹性模量200000MPa,
三节点竖向集中力均为100000N,
杆件横截面积4532mm2
桁架高度为3000mm
桁架横杆(包括底部受拉杆,顶部受拉杆)长度为3000mm
各节点坐标分别为[-4500, 0],[-1500,0],[1500,0],[4500,0],[-3000,3000],[0,3000],[3000,3000]
1.1 设定参数
import numpy as np
# from math import sqrt
import math
E = 200000
A = 4532
EA = E * A
scale_factor = 50
NodeCoord = np.array([[-4500, 0],[-1500,0],[1500,0],[4500,0],[-3000,3000],[0,3000],[3000,3000]])
# 七个节点
EleNode = np.array([[1,2],[2,3],[3,4],[5,6],[6,7],[1,5],[2,6],[3,7],[2,5],[3,6],[4,7]])
numEle = EleNode.shape[0]#单元总数
numNode = NodeCoord.shape[0]#节点总数
numDof = 2 * numNode# 自由度总数
forces = np.zeros((numDof,1))
stiffness = np.zeros((numDof,numDof))
restrainedDof = np.array([0,1,7])
xx = NodeCoord[:,[0]]
yy = NodeCoord[:,[1]]
forces[9] = forces[11] = forces[13] = -100000
1.2 求解整体刚度矩阵
##############################################################求解总刚矩阵
for i in range(numEle):
nodeIndex = EleNode[i,:]
delta_x = xx[nodeIndex[1]-1] - xx[nodeIndex[0]-1]
delta_y = yy[nodeIndex[1]-1] - yy[nodeIndex[0]-1]
L = math.sqrt(float(delta_x)**2 + float(delta_y)**2)
C = delta_x/L
S = delta_y/L
np.set_printoptions(precision=3)
eleK = EA/L *np.array([[C**2, C*S, -C**2, -C*S],[C*S, S**2, -C*S, -S**2],[-C**2, -C*S, C**2, C*S],[-C*S, -S**2, C*S, S**2]]).reshape(4,4)
ele_Dof_index = [2 * nodeIndex[0] - 1, 2 * nodeIndex[0], 2 * nodeIndex[1] - 1, 2 * nodeIndex[1]]
eleDof = np.array(ele_Dof_index)
stiff_Matrix_location = [(eleDof[i],eleDof[j]) for i in range(len(eleDof)) for j in range(len(eleDof))]
for j in range(len(stiff_Matrix_location)):
xy = stiff_Matrix_location[j]
eleKx = ele_Dof_index.index(xy[0])
eleKy = ele_Dof_index.index(xy[1])
# print('索引分别为',eleKx,eleKy,xy)
stiffness[(xy[0]-1,xy[1]-1)] += eleK[eleKx,eleKy]
# stiffness = stiffness.reshape(numDof,numDof)
# print(i)
# print(eleDof)
# print(stiffness)
stiffness_copy = stiffness.copy()# 复制一个总体刚度矩阵,后面备用
############################## 至此得到了总刚矩阵 stiffness
1.3 在Kx = F 中划掉约束自由度所在的行与列
list_Dof = np.arange(0,numDof)
activeDof = []
boolDof = []# 构造布尔数组,过滤受约束的行列
for i in list_Dof:
if i in restrainedDof:
boolDof.append(0)
continue
else:
boolDof.append(1)
activeDof.append(i)
# print(activeDof)
# print(boolDof)
boolDof = np.array(boolDof,dtype=np.bool)
stiffness = stiffness[boolDof,:]
stiffness = stiffness[:,boolDof]
forces = forces[boolDof,:]
1.4 求解 各节点x,y的位移
# 求解位移
# print(stiffness)
# print(forces)
# displacement = np.linalg.solve(stiffness,forces)
displacement = np.linalg.inv(stiffness).dot(forces)
print('displacement:')
print(displacement)
1.5 将位移0值添加到节点自由度受约束位置,即位移向量0,1,7位置
flag = 0
displacement = list(displacement)
while flag <len(restrainedDof):
displacement.insert(restrainedDof[flag],np.array([0]))
flag +=1
print('New_displacement:')
displacement = np.array(displacement)
displacement_copy = displacement.copy()
print(displacement)#
1.6 求解杆件轴力
TrussForce = np.zeros((numEle,1))
for i in range(numEle):
nodeIndex = EleNode[i,:]
delta_x = xx[nodeIndex[1]-1] - xx[nodeIndex[0]-1]
delta_y = yy[nodeIndex[1]-1] - yy[nodeIndex[0]-1]
L = math.sqrt(float(delta_x)**2 + float(delta_y)**2)
C = delta_x/L
S = delta_y/L
np.set_printoptions(precision=3)
ele_Dof_index = [2 * nodeIndex[0] - 2, 2 * nodeIndex[0]-1, 2 * nodeIndex[1] - 2, 2 * nodeIndex[1]-1]
TrussForce[i] = np.dot((EA/L)*np.array([-C,-S,C,S]).reshape(1,4) , displacement[ele_Dof_index])
print('TrussForce:','\n',TrussForce)
1.7 求解支座反力
reactionForce = np.zeros(len(restrainedDof))
for i in restrainedDof:
# print(stiffness_copy[i, :].reshape(1,14))
reactionForce[list(restrainedDof).index(i)] = np.dot(stiffness_copy[i, :].reshape(1, 14),displacement)
print('reactionForce:','\n',reactionForce)
1.8 绘制桁架变形图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
dispU = displacement[0:-1:2]
dispV = displacement[1::2]
formX = xx + dispU
deformY = yy + dispV
for i in range(numEle):
nodeIndex = EleNode[i,:]
x_loc = [xx[nodeIndex[0]-1],xx[nodeIndex[1]-1]]
y_loc = [yy[nodeIndex[0]-1],yy[nodeIndex[1]-1]]
plt.plot(x_loc,y_loc,'go:', label='Undeformed', linewidth=2)
for i in range(numEle):
nodeIndex = EleNode[i,:]
dx1 = scale_factor*dispU[nodeIndex[0]-1]
dx2 = scale_factor*dispU[nodeIndex[1]-1]
dy1 = scale_factor*dispV[nodeIndex[0]-1]
dy2 = scale_factor*dispV[nodeIndex[1]-1]
x_loc_deform = [xx[nodeIndex[0]-1]+dx1,xx[nodeIndex[1]-1]+dx2]
y_loc_deform = [yy[nodeIndex[0]-1]+dy1,yy[nodeIndex[1]-1]+dy2]
plt.plot(x_loc_deform,y_loc_deform,'ro-', label='Undeformed', linewidth=2)
plt.title('平面桁架Truss杆单元变形',fontsize=15)
plt.show()
1.9 桁架Truss杆单元变形图
2 通用有限元软件Ansys
2.1 参数设定及求解APDL命令
finish
/clear
/prep7
k,1,-4500,0,0
k,2,-1500,0,0
k,3,1500,0,0
k,4,4500,0,0
k,5,-3000,3000
k,6,0,3000,0
k,7,3000,3000,0
l,1,2
l,2,3
l,3,4
l,5,6
l,6,7
l,1,5
l,2,6
l,3,7
l,2,5
l,3,6
l,4,7
ET,1,LINK1
R,1,4532
MP,EX,1,2E5
MP,PRXY,1,0.3
LATT,1,1,1
LESIZE,ALL,,,1
LMESH,ALL
DK,1,UX,,,,UY
DK,4,UY
FORCES = 100000
FK,5,FY,-FORCES
FK,6,FY,-FORCES
FK,7,FY,-FORCES
/SOLU
ANTYPE,0
SOLVE
FINISH
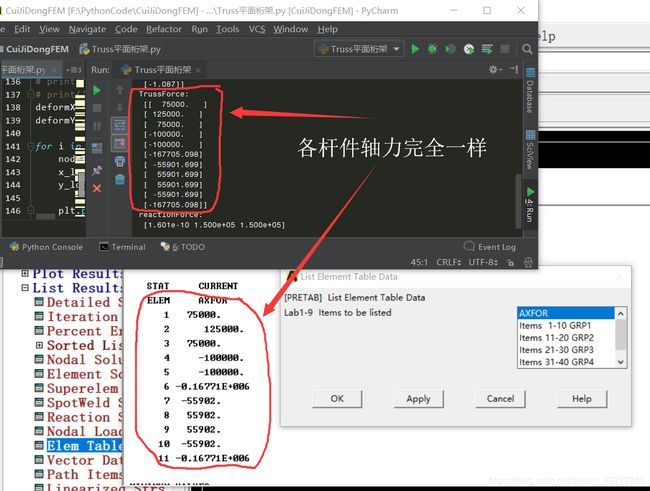
! 以下获取各杆件轴力
/post1
ETABLE,AXFOR,SMISC,1
PLLS,AXFOR,AXFOR,1
PLETAB,AXFOR
PLESOL,SMISC,1
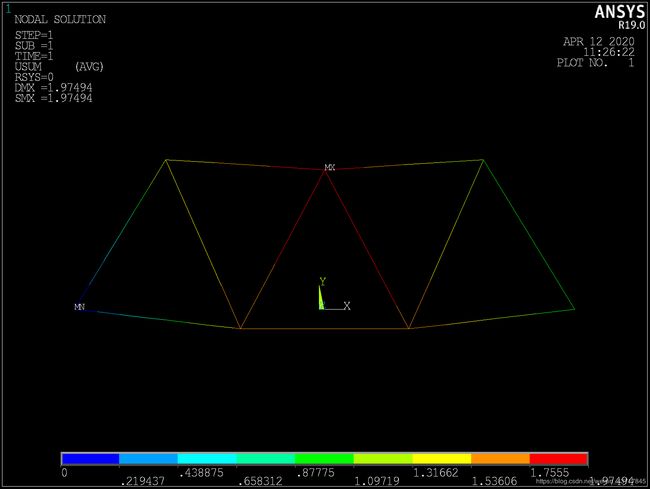
2.2 ANSYS 结果验证
2.3 各节点位移与杆件轴力 数据对比
2.3.1 结点位移
2.3.2 支座反力对比
左下节点1约束x y 向位移,右下节点4约束竖向y位移,得节点1水平约束力为0,竖向约束力为150000N