睿智的智能优化算法2——遗传算法的python实现
睿智的智能优化算法2——遗传算法的python实现
- 什么是遗传算法
- 求解过程
- 整体代码分解
- 1、编码解码部分
- 2、求取适应度部分
- 3、自然选择部分
- 4、组合交叉
- 5、基因突变
- 实现代码
- GITHUB下载连接
睿智的智能优化算法小课堂再次开课啦!
![]()
什么是遗传算法
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法的求解是从一个种群(population)开始的,而一个种群则由一定数目的个体(individual)组成。每个个体都是由基因(gene)编码(encoding)而成的,基因在编码之前实际上是个体的主要特征。
其实,遗传算法的执行过程就是通过一定编码方式将个体的特点进行编码形成基因,一个基因对应一个个体,一群个体组成一个种群。在进行编码的过程中,我们常用二进制进行编码。
初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解(不一定是最优的,接近最优的,优化算法基本上找到的都是接近最优的)。
在每一代,根据问题域中个体的适应度(fitness)大小,按照轮盘赌的方法选择(selection)个体,在完成选择后,还需要进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。
整个算法的过程就好像生物的优胜劣汰、自然进化一般,被称作遗传算法。
末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
求解过程
在遗传算法中,有几个必要而重要的概念,如下:
1、适应度,遗传算法中有一个种群,种群中有多个个体,每个个体根据其身上的特征,通过一定的运算,可以得到每个个体的适应度(fitness),适应度代表着这个个体对环境的适应情况,如果适应度高则在自然选择中更容易生存下来,即数据得到保留,参与后面的交叉繁殖和基因突变。
2、个体,遗传算法会通过一定编码方式将个体的特点进行编码形成基因,一个基因对应一个个体。
3、种群,一堆个体的集合,自然选择、组合交叉和基因突变的过程都在其内部进行。
4、自然选择,按照轮盘赌的方式,根据个体的适应度进行自然选择。其选择方式是这样的,如果个体1的适应度为2,个体2的适应度为1,那么选择到个体1个几率为2/(2+1)为66.67%。
5、组合交叉,选择基因内的一定结点,随机选择一个对象进行被选定结点的基因交换。交换示意图如下。
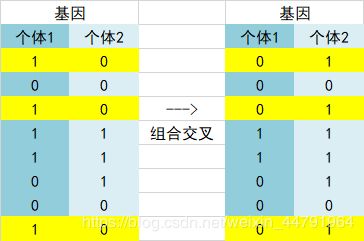
6、基因突变,选择基因内的一定结点,1突变成0,0突变为1。
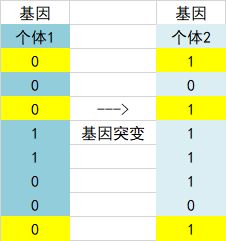
遗传算法的执行伪代码如下:
初始化种群pop
while 未达到最大迭代次数或最小loss:
for each_p in pop:
计算目标函数值
根据函数值计算适应度
选择其中的最佳适应度和网络结构存入bestresults
自然选择
组合交叉
基因突变
整体代码分解
1、编码解码部分
本文采用2进制编码,每个基因均为10位。
1101010101代表8.33。
11111111111代表10。
0000000000代表0。
由于没有必要完成十进制到二进制的转换,本文仅仅使用了解码函数,如下:
def binarytodecimal(binary): # 将二进制转化为十进制,x的范围是[0,10]
total = 0
for j in range(len(binary)):
total += binary[j] * (2**j)
total = total * 10 / 1023
return total
2、求取适应度部分
本文的例子求取的函数为sin(x) + cos(5x) - x^2 + 2*x
求取适应度部分的函数可以分为三个部分:
1、将整个种群转化为十进制。
2、将每个个体带入求取函数,得到目标函数值。
3、将目标函数值带入求适应度函数,求取适应度。
def pop_b2d(pop): # 将整个种群转化成二进制
temppop = []
for i in range(len(pop)):
t = binarytodecimal(pop[i])
temppop.append(t)
return temppop
def calobjvalue(pop): # 计算目标函数值
x = np.array(pop_b2d(pop))
return count_function(x)
def count_function(x):# 目标函数公式
y = np.sin(x) + np.cos(5 * x) - x**2 + 2*x
return y
def calfitvalue(objvalue):
# 转化为适应值,目标函数值越大越好
# 在本例子中可以直接使用函数运算结果为fit值,因为我们求的是最大值
# 在实际应用中需要进行一定的处理
# 去除0以下的适应值
for i in range(len(objvalue)):
if objvalue[i] < 0:
objvalue[i] = 0
return objvalue
3、自然选择部分
遗传算法采用轮盘赌进行自然选择。
每个个体可以根据其适应度计算其存活几率。
假设存在个体适应度分别为1,2,3,4,5的种群,个体1的存活几率为1/15,个体2的存活几率为2/15,以此类推,个体5的存活几率为5/15。
本文利用cum_sum表辅助自然选择个体。

实现代码为:
def selection(pop, fit_value):
probability_fit_value = []
# 适应度总和
total_fit = sum(fit_value)
# 求每个被选择的概率
probability_fit_value = np.array(fit_value) / total_fit
# 概率求和排序
cum_sum_table = cum_sum(probability_fit_value)
# 获取与pop大小相同的一个概率矩阵,其每一个内容均为一个概率
# 当概率处于不同范围时,选择不同的个体。
choose_probability = np.sort([np.random.rand() for i in range(len(pop))])
fitin = 0
newin = 0
newpop = pop[:]
# 轮盘赌法
while newin < len(pop):
# 当概率处于不同范围时,选择不同的个体。
# 如个体适应度分别为1,2,3,4,5的种群
# 利用np.random.rand()生成一个随机数,当其处于0-0.07时
# 选择个体1,当其属于0.07-0.2时选择个体2,以此类推。
if (choose_probability[newin] < cum_sum_table[fitin]):
newpop[newin] = pop[fitin]
newin = newin + 1
else:
fitin = fitin + 1
# pop里存在重复的个体
pop = newpop[:]
def cum_sum(fit_value):
# 输入[1, 2, 3, 4, 5],返回[1,3,6,10,15]
temp = fit_value[:]
temp2 = fit_value[:]
for i in range(len(temp)):
temp2[i] = (sum(temp[:i + 1]))
return temp2
4、组合交叉
def crossover(pop, pc):
# 按照一定概率杂交
pop_len = len(pop)
for i in range(pop_len - 1):
# 判断是否达到杂交几率
if (np.random.rand() < pc):
# 随机选取杂交点,然后交换结点的基因
individual_size = len(pop[0])
# 随机选择另一个个体进行杂交
destination = np.random.randint(0,pop_len)
# 生成每个基因进行交换的结点
crosspoint = np.random.randint(0,2,size = individual_size)
# 找到这些结点的索引
index = np.argwhere(crosspoint==1)
# 进行赋值
pop[i,index] = pop[destination,index]
5、基因突变
def mutation(pop, pm):
pop_len = len(pop)
individual_size = len(pop[0])
# 每条染色体随便选一个杂交
for i in range(pop_len):
for j in range(individual_size):
if (np.random.rand() < pm):
if (pop[i][j] == 1):
pop[i][j] = 0
else:
pop[i][j] = 1
实现代码
这是一个求取方程y = sin(x) + cos(5x) - x^2 + 2*x的最大值的例子。
import numpy as np
import math
import random
def binarytodecimal(binary): # 将二进制转化为十进制,x的范围是[0,10]
total = 0
for j in range(len(binary)):
total += binary[j] * (2**j)
total = total * 10 / 1023
return total
def pop_b2d(pop): # 将整个种群转化成十进制
temppop = []
for i in range(len(pop)):
t = binarytodecimal(pop[i])
temppop.append(t)
return temppop
def calobjvalue(pop): # 计算目标函数值
x = np.array(pop_b2d(pop))
return count_function(x)
def count_function(x):
y = np.sin(x) + np.cos(5 * x) - x**2 + 2*x
return y
def calfitvalue(objvalue):
# 转化为适应值,目标函数值越大越好
# 在本例子中可以直接使用函数运算结果为fit值,因为我们求的是最大值
# 在实际应用中需要处理
for i in range(len(objvalue)):
if objvalue[i] < 0:
objvalue[i] = 0
return objvalue
def best(pop, fitvalue):
#找出适应函数值中最大值,和对应的个体
bestindividual = pop[0]
bestfit = fitvalue[0]
for i in range(1,len(pop)):
if(fitvalue[i] > bestfit):
bestfit = fitvalue[i]
bestindividual = pop[i]
return [bestindividual, bestfit]
def selection(pop, fit_value):
probability_fit_value = []
# 适应度总和
total_fit = sum(fit_value)
# 求每个被选择的概率
probability_fit_value = np.array(fit_value) / total_fit
# 概率求和排序
cum_sum_table = cum_sum(probability_fit_value)
# 获取与pop大小相同的一个概率矩阵,其每一个内容均为一个概率
# 当概率处于不同范围时,选择不同的个体。
choose_probability = np.sort([np.random.rand() for i in range(len(pop))])
fitin = 0
newin = 0
newpop = pop[:]
# 轮盘赌法
while newin < len(pop):
# 当概率处于不同范围时,选择不同的个体。
# 如个体适应度分别为1,2,3,4,5的种群
# 利用np.random.rand()生成一个随机数,当其处于0-0.07时
# 选择个体1,当其属于0.07-0.2时选择个体2,以此类推。
if (choose_probability[newin] < cum_sum_table[fitin]):
newpop[newin] = pop[fitin]
newin = newin + 1
else:
fitin = fitin + 1
# pop里存在重复的个体
pop = newpop[:]
def cum_sum(fit_value):
# 输入[1, 2, 3, 4, 5],返回[1,3,6,10,15]
temp = fit_value[:]
temp2 = fit_value[:]
for i in range(len(temp)):
temp2[i] = (sum(temp[:i + 1]))
return temp2
def crossover(pop, pc):
# 按照一定概率杂交
pop_len = len(pop)
for i in range(pop_len - 1):
# 判断是否达到杂交几率
if (np.random.rand() < pc):
# 随机选取杂交点,然后交换结点的基因
individual_size = len(pop[0])
# 随机选择另一个个体进行杂交
destination = np.random.randint(0,pop_len)
# 生成每个基因进行交换的结点
crosspoint = np.random.randint(0,2,size = individual_size)
# 找到这些结点的索引
index = np.argwhere(crosspoint==1)
# 进行赋值
pop[i,index] = pop[destination,index]
def mutation(pop, pm):
pop_len = len(pop)
individual_size = len(pop[0])
# 每条染色体随便选一个杂交
for i in range(pop_len):
for j in range(individual_size):
if (np.random.rand() < pm):
if (pop[i][j] == 1):
pop[i][j] = 0
else:
pop[i][j] = 1
# 用遗传算法求函数最大值,组合交叉的概率时0.6,突变的概率为0.001
# y = np.sin(x) + np.cos(5 * x) - x**2 + 2*x
popsize = 50 # 种群的大小
pc = 0.6 # 两个个体交叉的概率
pm = 0.001 # 基因突变的概率
gene_size = 10 # 基因长度为10
generation = 100 # 繁殖100代
results = []
bestindividual = []
bestfit = 0
fitvalue = []
pop = np.array([np.random.randint(0,2,size = gene_size) for i in range(popsize)])
for i in range(generation): # 繁殖100代
objvalue = calobjvalue(pop) # 计算种群中目标函数的值
fitvalue = calfitvalue(objvalue) # 计算个体的适应值
[bestindividual, bestfit] = best(pop, fitvalue) # 选出最好的个体和最好的适应值
results.append([bestfit,binarytodecimal(bestindividual)]) # 每次繁殖,将最好的结果记录下来
selection(pop, fitvalue) # 自然选择,淘汰掉一部分适应性低的个体
crossover(pop, pc) # 交叉繁殖
mutation(pop, pc) # 基因突变
results.sort()
print(results[-1]) #打印使得函数取得最大的个体,和其对应的适应度
实现结果为:
[2.8858902330957323, 1.2512218963831867]
GITHUB下载连接
https://github.com/bubbliiiing/Optimization_Algorithm
希望得到朋友们的喜欢。
有问题的朋友可以提问噢。