NSGA-Ⅱ算法C++实现(测试函数为ZDT1)
在看C++实现之前,请先看一下NSGA-II算法概述
http://www.omegaxyz.com/2017/04/14/nsga-iiintro/
NSGA-Ⅱ就是在第一代非支配排序遗传算法的基础上改进而来,其改进主要是针对如上所述的三个方面:
①提出了快速非支配排序算法,一方面降低了计算的复杂度,另一方面它将父代种群跟子代种群进行合并,使得下一代的种群从双倍的空间中进行选取,从而保留了最为优秀的所有个体;
②引进精英策略,保证某些优良的种群个体在进化过程中不会被丢弃,从而提高了优化结果的精度;
③采用拥挤度和拥挤度比较算子,不但克服了NSGA中需要人为指定共享参数的缺陷,而且将其作为种群中个体间的比较标准,使得准Pareto域中的个体能均匀地扩展到整个Pareto域,保证了种群的多样性。
头文件:
#include个体的类声明:
class individual
{
public:
double value[Dimension];//xi的值
int sp[2*popsize];
//被支配个体集合SP。该量是可行解空间中所有被个体p支配的个体组成的集合。
int np;
//支配个数np。该量是在可行解空间中可以支配个体p的所以个体的数量。
int is_dominated;//集合sp的个数
void init();//初始化个体
int rank;//优先级,Pareto级别为当前最高级
double crowding_distance;//拥挤距离
double fvalue[2];//ZDT1问题目标函数的值
void f_count();//计算fvalue的值
};群体的类声明:
class population
{
public:
population();//类初始化
individual P[popsize];
individual Q[popsize];
individual R[2*popsize];
void set_p_q();
//随机产生一个初始父代P,在此基础上采用二元锦标赛选择、
//交叉和变异操作产生子代Q。P和Q群体规模均为popsize
//将Pt和Qt并入到Rt中(初始时t=0),对Rt进行快速非支配解排序,
//构造其所有不同等级的非支配解集F1、F2........
int Rnum;
int Pnum;
int Qnum;
//P,Q,R中元素的个数
void make_new_pop();//产生新的子代
void fast_nondominated_sort();//快速非支配排序
void calu_crowding_distance(int i);//拥挤距离计算
void f_sort(int i);//对拥挤距离降序排列
void maincal();//主要操作
int choice(int a,int b);
//两个个体属于不同等级的非支配解集,优先考虑等级序号较小的
//若两个个体属于同一等级的非支配解集,优先考虑拥挤距离较大的
int len[2*popsize];//各个变异交叉后的群体Fi的长度的集合
int len_f;//整个群体rank值
};全局变量及部分函数声明:
individual F[2*popsize][2*popsize];
double rand_real(double low,double high)
//产生随机实数
{
double h;
h=(high-low)*URAND+low+0.001;
if(h>=high)
h=high-0.001;
return h;
}
int rand_int(int low,int high)
//产生随机整数
{
return int((high-low+1)*URAND)+low;
}关于排序函数qsort
void qsort( void *base, size_t num, size_t width, int (__cdecl *compare )
利用qsort对F[i]数组按照cmp3排序
int cmp1(const void *a,const void *b)
//目标函数f1的升序排序
{
const individual *e=(const individual *)a;
const individual *f=(const individual *)b;
if(e->fvalue[0]==f->fvalue[0])
return 0;
else if(e->fvalue[0]fvalue[0])
return -1;
else return 1;
}
int cmp2(const void *a,const void *b)
//目标函数f2的升序排序
{
const individual *e=(const individual *)a;
const individual *f=(const individual *)b;
if(e->fvalue[1]==f->fvalue[1])
return 0;
else if(e->fvalue[1]fvalue[1])
return -1;
else return 1;
}
int cmp_c_d(const void *a,const void *b)
//对拥挤距离降序排序
{
const individual *e=(const individual *)a;
const individual *f=(const individual *)b;
if(e->crowding_distance==f->crowding_distance)
return 0;
else if(e->crowding_distancecrowding_distance)
return 1;
else
return -1;
}
void population::f_sort(int i)
{
int n;
n=len[i];
qsort(F[i],n,sizeof(individual),cmp_c_d);
} 群的初始化:
population::population()
{
int i;
for(i=0;i
for(i=0;ii ++)
{
P[i].f_count();
}
Pnum=popsize;
Qnum=0;
Rnum=0;
}个体初始化:
void individual::init()
{
for(int i=0;ivalue[i]=rand_real(0.0,1.0);
} 利用二进制锦标赛产生子代:
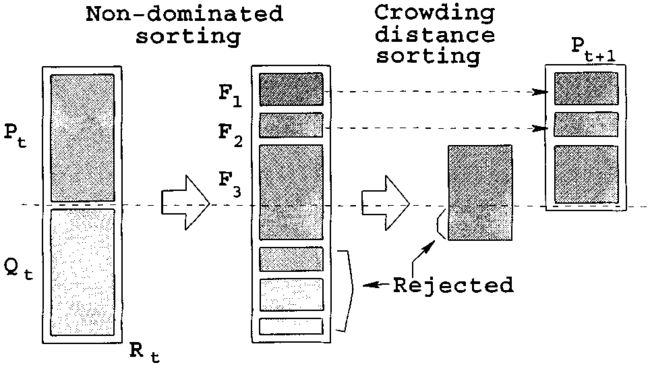
1、随机产生一个初始父代Po,在此基础上采用二元锦标赛选择、交叉和变异操作产生子代Qo, Po 和Qo群体规模均为N
2、将Pt和Qt并入到Rt中(初始时t=0),对Rt进行快速非支配解排序,构造其所有不同等级的非支配解集F1、F2……..
3、按照需要计算Fi中所有个体的拥挤距离,并根据拥挤比较运算符构造Pt+1,直至Pt+1规模为N,图中的Fi为F3
void population::make_new_pop()
{
int i,j,x,y,t1,t2,t3;
double s,u,b;
memset(mark,0,sizeof(mark));
t3=0;
while(t32)
{
while(t1=t2=rand_int(0,popsize-1),mark[t1]);
while(t1==t2||mark[t2])
{
t2=rand_int(0,popsize-1);
}
t1=choice(t1,t2);
temp1[t3++]=t1;
mark[t1]=1;
}
for(i=0;i0.0,1.0);
if(s<=0.9)
{
for(j=0;j0.0+1e-6),(1.0-1e-6));
if(u<=0.5)
b=pow(2*u,1.0/21);
else
b=1.0/pow(2*(1-u),1.0/21);
x=y=rand_int(0,popsize/2-1);
while(x==y)
y=rand_int(0,popsize/2-1);
Q[i].value[j]=1.0/2*((1-b)*P[temp1[x]].value[j]+(1+b)*P[temp1[y]].value[j]);
if(Q[i].value[j]<0)
Q[i].value[j]=1e-6;
else if(Q[i].value[j]>1)
Q[i].value[j]=1.0-(1e-6);
if(i+11].value[j]=1.0/2*((1+b)*P[temp1[x]].value[j]+(1-b)*P[temp1[y]].value[j]);
if(Q[i+1].value[j]<=0)
Q[i+1].value[j]=1e-6;
else if(Q[i+1].value[j]>1)
Q[i+1].value[j]=(1-1e-6);
}
}
i++;
}
else
{
for(j=0;j0,popsize/2-1);
u=rand_real(0.0+(1e-6),1.0-(1e-6));
if(u<0.5)
u=pow(2*u,1.0/21)-1;
else
u=1-pow(2*(1-u),1.0/21);
Q[i].value[j]=P[temp1[x]].value[j]+(1.0-0.0)*u;
if(Q[i].value[j]<0)
Q[i].value[j]=1e-6;
else if(Q[i].value[j]>1)
Q[i].value[j]=1-(1e-6);
}
}
}
Qnum=popsize;
for(i=0;ivoid population::set_p_q()
{
Rnum=0;
Qnum=popsize;
int i;
for(i=0;ifor(i=0;ifor(i=0;i<2*popsize;i++)
R[i].f_count();
}
void population::set_p_q()
{
Rnum=0;
Qnum=popsize;
int i;
for(i=0;ifor(i=0;ifor(i=0;i<2*popsize;i++)
R[i].f_count();
} ZDT1问题函数值的计算:
void individual::f_count()
{
fvalue[0]=value[0];
int i;
double g=1,sum=0;
for(i=1;isum+=value[i];
}
sum+=9*(sum/(Dimension-1));
g+=sum;
fvalue[1]=g*(1-sqrt(value[0]/g));
} 判断目标函数值是否被支配:
bool e_is_dominated(const individual &a,const individual &b)
{
if((a.fvalue[0]<=b.fvalue[0])&&(a.fvalue[1]<=b.fvalue[1]))
{
if((a.fvalue[0]==b.fvalue[0])&&a.fvalue[1]==b.fvalue[1])
return false;
else
return true;
}
else
return false;
}快速非支配排序法:重点!!!
void population::fast_nondominated_sort()
{
int i,j,k;
individual H[2*popsize];
int h_len=0;
for(i=0;i<2*popsize;i++)
{
R[i].np=0;
R[i].is_dominated=0;
len[i]=0;
}
for(i=0;i<2*popsize;i++)
{
for(j=0;j<2*popsize;j++)
{
if(i!=j)
{
if(e_is_dominated(R[i],R[j]))
R[i].sp[R[i].is_dominated++]=j;
else if(e_is_dominated(R[j],R[i]))
R[i].np+=1;
}
}
if(R[i].np==0)
{
len_f=1;
F[0][len[0]++]=R[i];
}
}
i=0;
while(len[i]!=0)
{
h_len=0;
for(j=0;j
{
for(k=0;k
{
R[F[i][j].sp[k]].np--;
if(R[F[i][j].sp[k]].np==0)
{
H[h_len++]=R[F[i][j].sp[k]];
R[F[i][j].sp[k]].rank=i+2;
}
}
}
i++;
len[i]=h_len;
if(h_len!=0)
{
len_f++;
for(j=0;j
F[i][j]=H[j];
}
}
} 计算拥挤距离:重点!!!具体解释见其他文章!!!
void population::calu_crowding_distance(int i)
{
int n=len[i];
double m_max,m_min;
int j;
for(j=0;jF[i][j].crowding_distance=0;
F[i][0].crowding_distance=F[i][n-1].crowding_distance=0xffffff;
qsort(F[i],n,sizeof(individual),cmp1);
m_max=-0xfffff;
m_min=0xfffff;
for(j=0;jif(m_max<F[i][j].fvalue[0])
m_max=F[i][j].fvalue[0];
if(m_min>F[i][j].fvalue[0])
m_min=F[i][j].fvalue[0];
}
for(j=1;j1;j++)
F[i][j].crowding_distance+=(F[i][j+1].fvalue[0]-F[i][j-1].fvalue[0])/(m_max-m_min);
F[i][0].crowding_distance=F[i][n-1].crowding_distance=0xffffff;
qsort(F[i],n,sizeof(individual),cmp2);
m_max=-0xfffff;
m_min=0xfffff;
for(j=0;jif(m_max<F[i][j].fvalue[1])
m_max=F[i][j].fvalue[1];
if(m_min>F[i][j].fvalue[1])
m_min=F[i][j].fvalue[1];
}
for(j=1;j1;j++)
F[i][j].crowding_distance+=(F[i][j+1].fvalue[1]-F[i][j-1].fvalue[1])/(m_max-m_min);
} 采集多样性的选择:
int population::choice(int a,int b)
{
if(P[a].rankreturn a;
else if(P[a].rank==P[b].rank)
{
if(P[a].crowding_distance>P[b].crowding_distance)
return a;
else
return b;
}
else
return b;
} 主要操作函数:
void population::maincal()
{
int s,i,j;
s=generation;
make_new_pop();
while(s--)
{
printf("The %d generation\n",s);
set_p_q();
fast_nondominated_sort();
Pnum=0;
i=0;
while(Pnum+len[i]<=popsize)
{
calu_crowding_distance(i);
for(j=0;jif(i>=len_f)break;
}
if(ifor(j=0;j 主函数:
int main()
{
FILE *p;
p=fopen("d:\\My_NSGA2.txt","w+");
srand((unsigned int)(time(0)));
population pop;
pop.maincal();
int i,j;
fprintf(p,"XuYi All Rights Reserved.\nWelcome to OmegaXYZ: www.omegaxyz.com\n");
fprintf(p,"Problem ZDT1\n");
fprintf(p,"\n");
for(i=0;i"The %d generation situation:\n",i);
for(j=1;j<=Dimension;j++)
{
fprintf(p,"x%d=%e ",j,pop.P[i].value[j]);
}
fprintf(p,"\n");
fprintf(p,"f1(x)=%f f2(x)=%f\n",pop.P[i].fvalue[0],pop.P[i].fvalue[1]);
}
fclose(p);
return 1;
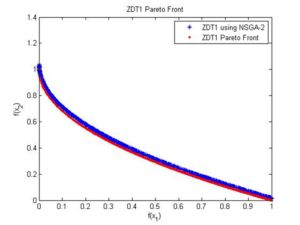
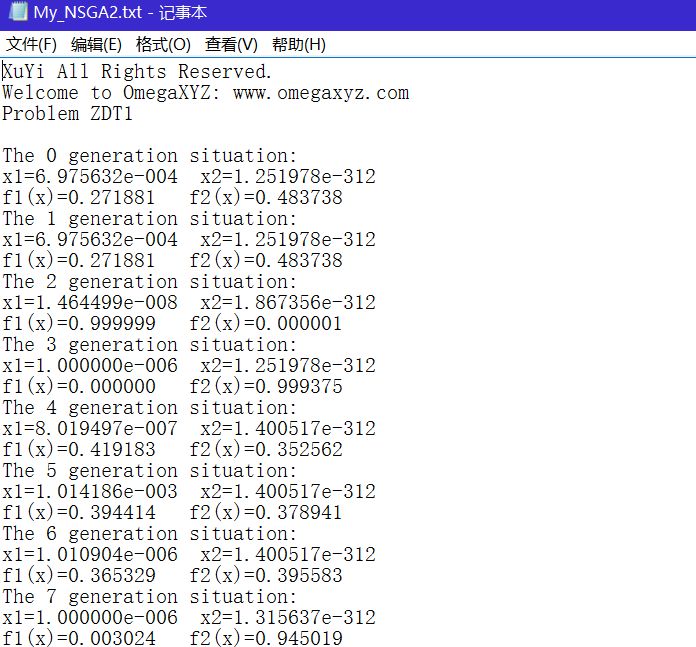
} ZDT1问题图像及前沿面。
快速支配排序具体解释见多目标算法NSGA-II:http://www.omegaxyz.com/2017/04/19/nsga2fastsort/
多目标问题解释:http://www.omegaxyz.com/2017/04/16/theexpofpareto/