NSGA2算法MATLAB
NSGA2算法MATLAB实现(能够自定义优化函数)
以前写了一个简单的NSGA2的算法能够用在ZDT1函数上:http://www.omegaxyz.com/2017/05/04/nsga2matlabzdt1/
那个NSGA2的算法不具有普遍性,下面参考课国外的课题小组的代码重新修改了内部冗余内容,使之能够自定义优化函数。

更多内容访问omegaxyz.com
NSGA2的过程为:
1、随机产生一个初始父代Po,在此基础上采用二元锦标赛选择、交叉和变异操作产生子代Qo, Po 和Qo群体规模均为N
2、将Pt和Qt并入到Rt中(初始时t=0),对Rt进行快速非支配解排序,构造其所有不同等级的非支配解集F1、F2……..
3、按照需要计算Fi中所有个体的拥挤距离,并根据拥挤比较运算符构造Pt+1,直至Pt+1规模为N,图中的Fi为F3
具体解释请见:http://www.omegaxyz.com/2017/04/14/nsga-iiintro/
C++代码请见(测试函数ZDT1):http://www.omegaxyz.com/2017/04/20/nsga2zdt1/
下面是完整版的代码:
①nsga2-optimization.m
function nsga_2_optimization
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%此处可以更改
%更多机器学习内容请访问omegaxyz.com
pop = 500; %种群数量
gen = 500; %迭代次数
M = 2; %目标数量
V = 30; %维度
min_range = zeros(1, V); %下界
max_range = ones(1,V); %上界
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
chromosome = initialize_variables(pop, M, V, min_range, max_range);
chromosome = non_domination_sort_mod(chromosome, M, V);
for i = 1 : gen
pool = round(pop/2);
tour = 2;
parent_chromosome = tournament_selection(chromosome, pool, tour);
mu = 20;
mum = 20;
offspring_chromosome = genetic_operator(parent_chromosome,M, V, mu, mum, min_range, max_range);
[main_pop,~] = size(chromosome);
[offspring_pop,~] = size(offspring_chromosome);
clear temp
intermediate_chromosome(1:main_pop,:) = chromosome;
intermediate_chromosome(main_pop + 1 : main_pop + offspring_pop,1 : M+V) = offspring_chromosome;
intermediate_chromosome = non_domination_sort_mod(intermediate_chromosome, M, V);
chromosome = replace_chromosome(intermediate_chromosome, M, V, pop);
if ~mod(i,100)
clc;
fprintf('%d generations completed\n',i);
end
end
if M == 2
plot(chromosome(:,V + 1),chromosome(:,V + 2),'*');
xlabel('f_1'); ylabel('f_2');
title('Pareto Optimal Front');
elseif M == 3
plot3(chromosome(:,V + 1),chromosome(:,V + 2),chromosome(:,V + 3),'*');
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
title('Pareto Optimal Surface');
end②initialize_variables.m
function f = initialize_variables(N, M, V, min_range, max_range)
min = min_range;
max = max_range;
K = M + V;
for i = 1 : N
for j = 1 : V
f(i,j) = min(j) + (max(j) - min(j))*rand(1);
end
f(i,V + 1: K) = evaluate_objective(f(i,:), M, V);
end③non_domination_sort_mod.m
function f = non_domination_sort_mod(x, M, V)
[N, ~] = size(x);
clear m
front = 1;
F(front).f = [];
individual = [];
for i = 1 : N
individual(i).n = 0;
individual(i).p = [];
for j = 1 : N
dom_less = 0;
dom_equal = 0;
dom_more = 0;
for k = 1 : M
if (x(i,V + k) < x(j,V + k))
dom_less = dom_less + 1;
elseif (x(i,V + k) == x(j,V + k))
dom_equal = dom_equal + 1;
else
dom_more = dom_more + 1;
end
end
if dom_less == 0 && dom_equal ~= M
individual(i).n = individual(i).n + 1;
elseif dom_more == 0 && dom_equal ~= M
individual(i).p = [individual(i).p j];
end
end
if individual(i).n == 0
x(i,M + V + 1) = 1;
F(front).f = [F(front).f i];
end
end
while ~isempty(F(front).f)
Q = [];
for i = 1 : length(F(front).f)
if ~isempty(individual(F(front).f(i)).p)
for j = 1 : length(individual(F(front).f(i)).p)
individual(individual(F(front).f(i)).p(j)).n = ...
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0
x(individual(F(front).f(i)).p(j),M + V + 1) = ...
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end
[temp,index_of_fronts] = sort(x(:,M + V + 1));
for i = 1 : length(index_of_fronts)
sorted_based_on_front(i,:) = x(index_of_fronts(i),:);
end
current_index = 0;
%% Crowding distance
for front = 1 : (length(F) - 1)
distance = 0;
y = [];
previous_index = current_index + 1;
for i = 1 : length(F(front).f)
y(i,:) = sorted_based_on_front(current_index + i,:);
end
current_index = current_index + i;
sorted_based_on_objective = [];
for i = 1 : M
[sorted_based_on_objective, index_of_objectives] = ...
sort(y(:,V + i));
sorted_based_on_objective = [];
for j = 1 : length(index_of_objectives)
sorted_based_on_objective(j,:) = y(index_of_objectives(j),:);
end
f_max = ...
sorted_based_on_objective(length(index_of_objectives), V + i);
f_min = sorted_based_on_objective(1, V + i);
y(index_of_objectives(length(index_of_objectives)),M + V + 1 + i)...
= Inf;
y(index_of_objectives(1),M + V + 1 + i) = Inf;
for j = 2 : length(index_of_objectives) - 1
next_obj = sorted_based_on_objective(j + 1,V + i);
previous_obj = sorted_based_on_objective(j - 1,V + i);
if (f_max - f_min == 0)
y(index_of_objectives(j),M + V + 1 + i) = Inf;
else
y(index_of_objectives(j),M + V + 1 + i) = ...
(next_obj - previous_obj)/(f_max - f_min);
end
end
end
distance = [];
distance(:,1) = zeros(length(F(front).f),1);
for i = 1 : M
distance(:,1) = distance(:,1) + y(:,M + V + 1 + i);
end
y(:,M + V + 2) = distance;
y = y(:,1 : M + V + 2);
z(previous_index:current_index,:) = y;
end
f = z();④tournament_selection.m
function f = tournament_selection(chromosome, pool_size, tour_size)
[pop, variables] = size(chromosome);
rank = variables - 1;
distance = variables;
for i = 1 : pool_size
for j = 1 : tour_size
candidate(j) = round(pop*rand(1));
if candidate(j) == 0
candidate(j) = 1;
end
if j > 1
while ~isempty(find(candidate(1 : j - 1) == candidate(j)))
candidate(j) = round(pop*rand(1));
if candidate(j) == 0
candidate(j) = 1;
end
end
end
end
for j = 1 : tour_size
c_obj_rank(j) = chromosome(candidate(j),rank);
c_obj_distance(j) = chromosome(candidate(j),distance);
end
min_candidate = ...
find(c_obj_rank == min(c_obj_rank));
if length(min_candidate) ~= 1
max_candidate = ...
find(c_obj_distance(min_candidate) == max(c_obj_distance(min_candidate)));
if length(max_candidate) ~= 1
max_candidate = max_candidate(1);
end
f(i,:) = chromosome(candidate(min_candidate(max_candidate)),:);
else
f(i,:) = chromosome(candidate(min_candidate(1)),:);
end
end⑤genetic_operator.m
function f = genetic_operator(parent_chromosome, M, V, mu, mum, l_limit, u_limit)
[N,m] = size(parent_chromosome);
clear m
p = 1;
was_crossover = 0;
was_mutation = 0;
for i = 1 : N
% With 90 % probability perform crossover
if rand(1) < 0.9
% Initialize the children to be null vector.
child_1 = [];
child_2 = [];
% Select the first parent
parent_1 = round(N*rand(1));
if parent_1 < 1
parent_1 = 1;
end
% Select the second parent
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
% Make sure both the parents are not the same.
while isequal(parent_chromosome(parent_1,:),parent_chromosome(parent_2,:))
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
end
% Get the chromosome information for each randomnly selected
% parents
parent_1 = parent_chromosome(parent_1,:);
parent_2 = parent_chromosome(parent_2,:);
% Perform corssover for each decision variable in the chromosome.
for j = 1 : V
% SBX (Simulated Binary Crossover).
% For more information about SBX refer the enclosed pdf file.
% Generate a random number
u(j) = rand(1);
if u(j) <= 0.5
bq(j) = (2*u(j))^(1/(mu+1));
else
bq(j) = (1/(2*(1 - u(j))))^(1/(mu+1));
end
% Generate the jth element of first child
child_1(j) = ...
0.5*(((1 + bq(j))*parent_1(j)) + (1 - bq(j))*parent_2(j));
% Generate the jth element of second child
child_2(j) = ...
0.5*(((1 - bq(j))*parent_1(j)) + (1 + bq(j))*parent_2(j));
% Make sure that the generated element is within the specified
% decision space else set it to the appropriate extrema.
if child_1(j) > u_limit(j)
child_1(j) = u_limit(j);
elseif child_1(j) < l_limit(j)
child_1(j) = l_limit(j);
end
if child_2(j) > u_limit(j)
child_2(j) = u_limit(j);
elseif child_2(j) < l_limit(j)
child_2(j) = l_limit(j);
end
end
child_1(:,V + 1: M + V) = evaluate_objective(child_1, M, V);
child_2(:,V + 1: M + V) = evaluate_objective(child_2, M, V);
was_crossover = 1;
was_mutation = 0;
% With 10 % probability perform mutation. Mutation is based on
% polynomial mutation.
else
% Select at random the parent.
parent_3 = round(N*rand(1));
if parent_3 < 1
parent_3 = 1;
end
% Get the chromosome information for the randomnly selected parent.
child_3 = parent_chromosome(parent_3,:);
% Perform mutation on eact element of the selected parent.
for j = 1 : V
r(j) = rand(1);
if r(j) < 0.5
delta(j) = (2*r(j))^(1/(mum+1)) - 1;
else
delta(j) = 1 - (2*(1 - r(j)))^(1/(mum+1));
end
% Generate the corresponding child element.
child_3(j) = child_3(j) + delta(j);
% Make sure that the generated element is within the decision
% space.
if child_3(j) > u_limit(j)
child_3(j) = u_limit(j);
elseif child_3(j) < l_limit(j)
child_3(j) = l_limit(j);
end
end
child_3(:,V + 1: M + V) = evaluate_objective(child_3, M, V);
% Set the mutation flag
was_mutation = 1;
was_crossover = 0;
end
if was_crossover
child(p,:) = child_1;
child(p+1,:) = child_2;
was_cossover = 0;
p = p + 2;
elseif was_mutation
child(p,:) = child_3(1,1 : M + V);
was_mutation = 0;
p = p + 1;
end
end
f = child;⑥replace_chromosome.m
function f = replace_chromosome(intermediate_chromosome, M, V,pop)
[N, m] = size(intermediate_chromosome);
% Get the index for the population sort based on the rank
[temp,index] = sort(intermediate_chromosome(:,M + V + 1));
clear temp m
% Now sort the individuals based on the index
for i = 1 : N
sorted_chromosome(i,:) = intermediate_chromosome(index(i),:);
end
% Find the maximum rank in the current population
max_rank = max(intermediate_chromosome(:,M + V + 1));
% Start adding each front based on rank and crowing distance until the
% whole population is filled.
previous_index = 0;
for i = 1 : max_rank
% Get the index for current rank i.e the last the last element in the
% sorted_chromosome with rank i.
current_index = max(find(sorted_chromosome(:,M + V + 1) == i));
% Check to see if the population is filled if all the individuals with
% rank i is added to the population.
if current_index > pop
% If so then find the number of individuals with in with current
% rank i.
remaining = pop - previous_index;
% Get information about the individuals in the current rank i.
temp_pop = ...
sorted_chromosome(previous_index + 1 : current_index, :);
% Sort the individuals with rank i in the descending order based on
% the crowding distance.
[temp_sort,temp_sort_index] = ...
sort(temp_pop(:, M + V + 2),'descend');
% Start filling individuals into the population in descending order
% until the population is filled.
for j = 1 : remaining
f(previous_index + j,:) = temp_pop(temp_sort_index(j),:);
end
return;
elseif current_index < pop
% Add all the individuals with rank i into the population.
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
else
% Add all the individuals with rank i into the population.
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
return;
end
% Get the index for the last added individual.
previous_index = current_index;
end⑦自定义评价函数(我选用的ZDT1函数)
function f = evaluate_objective(x, M, V)
f = [];
f(1) = x(1);
g = 1;
sum = 0;
for i = 1:V
sum = sum + x(i);
end
sum = sum + 9*(sum / (V-1));
g = g + sum;
f(2) = g * (1 - sqrt(x(1) / g));
end500个种群运行500代的结果:
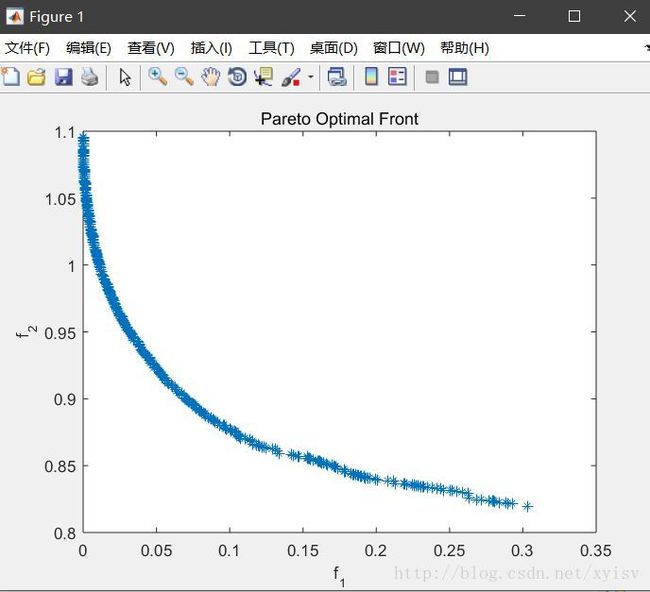

代码打包下载:http://download.csdn.net/download/xyisv/10217700
更多内容访问omegaxyz.com
网站文章采用知识共享许可协议BY-NC-SA4.0授权
© 2018 • OmegaXYZ-版权所有 转载请注明出处