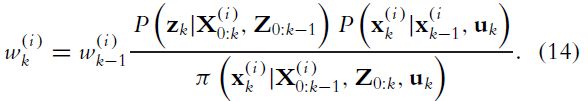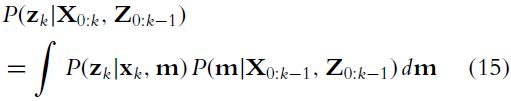科研笔记(二) 一篇文章带你走进SLAM的前半生
Hello,everyone!
我是CS科研GO,一个热衷于科研和软开的胖子!
论文题目:Simultaneous Localization and Mapping: Part I
论文作者:Hugh Durrant-Whyte,Tim Bailey;工作单位:悉尼大学,澳大利亚;
发表期刊:IEEE ROBOTICS & AUTOMATION MAGAZINE(SCI二区)。
话不多说,先来张SLAM效果图
这篇早期很有名气的SLAM综述性论文,发表于2006年。主要内容如下:
- 一、SLAM的早期发展史
- 1.1 SLAM问题起源
- 1.2 理论发展受阻
- 1.3 理论突破
- 1.4 理论改进
- 1.5 研究热点
- 二、SLAM理论及演变过程
- 2.1 预备知识
- 2.2 SLAM问题的概率分布
- 2.3 SLAM概率分布讨论
- 三、SLAM解决方案
- 3.1 EKF-SLAM
- 3.2 FastSLAM
- 四、SLAM实现
一、SLAM的早期发展史
1.1 SLAM问题起源
SLAM问题起源于1986年举行的IEEE Robotics and Automation Conference (San Francisco, California)。会议结束后,参会的研究人员做了许多相关的理论工作。
1.2 理论发展受阻
1990年,Smith等人的研究表明,对于定位和地图构建问题的完整解决方案需要估算机器人(载具)姿态和每个地标位置组成的联合状态,并在每次观察地标之后进行更新。这将要求估算函数采用复杂的状态向量(按地图中维护的地标数量的顺序),计算规模为地标数量的平方。此外,这项工作没有考虑地图映射的收敛性或稳定性,这意味着问题的计算复杂度很高,而且地图估计的误差不会收敛。
1.3 理论突破
1997年,Univ. Oxford博士生M. Csorba给出了SLAM问题的收敛性理论和初始结果。
1.4 理论改进
在97年的理论工作基础上,研究人员关注改进计算能效性,解决数据关联和回环问题。1999年International Symposium on Robotics Research (ISRR)首次举办SLAM研讨会,S. Thrun等人将基于Kalman滤波器的SLAM方法与概率定位和映射方法进行了一定程度的融合。
1.5 研究热点
2002年,ICRA的SLAM研讨会吸引了150位兴趣广泛的研究人员;由H. Christiansen同年举办的SLAM暑期学校吸引了来自世界各地的重要研究人员和50名博士生,在此领域的建设上取得了巨大影响。
二、SLAM理论及演变过程
SLAM是一个过程,移动机器人可以通过该过程构建环境地图,并同时使用该地图推断其位置。在SLAM中,无需任何先验位置知识即可在线估算机器人的轨迹和所有地标的位置。
2.1 预备知识
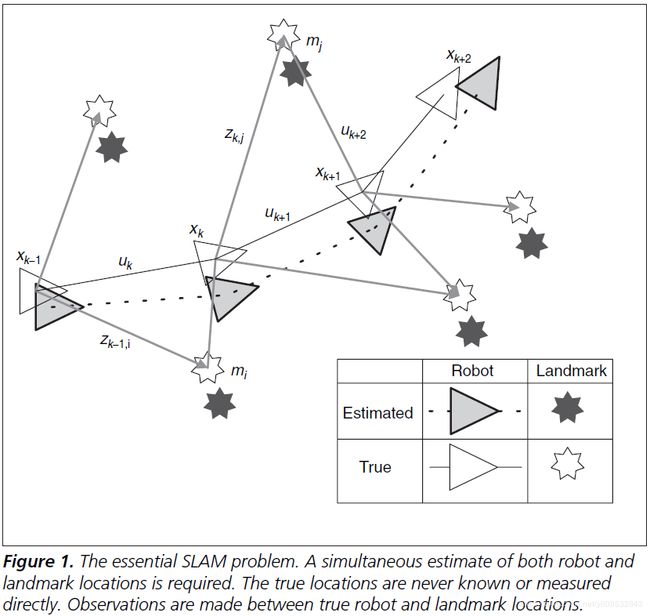
图1描述一个基本的SLAM过程。在时刻 t t t,定义以下变量:
- x k x_k xk: 描述机器人(载具)位置和方向的状态向量;
- u k u_k uk: 控制向量,用于描述机器人从 t − 1 t-1 t−1时刻到 t t t时刻的变化;
- m i m_i mi: 描述第 i i i个地标位置的向量,假定地标位置不随时间发生改变;
- z i k z_{ik} zik: 在 k k k时刻,机器人对第 i i i个地标位置的观测值;若此时观测到多个地标,或无需关注的地标,则用 z k z_k zk表示。
此外,定义以下集合:
- X 0 : k = { x 0 , x 1 , … x k } = { X 0 : k − 1 , x k } X_{0: k}=\left\{x_{0}, x_{1}, \ldots x_{k}\right\}=\left\{X_{0: k-1}, x_{k}\right\} X0:k={x0,x1,…xk}={X0:k−1,xk}: 表示机器人的历史位置;
- U 0 : k = { u 1 , u 2 … u k } = { U 0 : k − 1 , u k } U_{0: k}=\left\{u_{1}, u_{2} \ldots u_{k}\right\}=\left\{U_{0: k-1}, u_{k}\right\} U0:k={u1,u2…uk}={U0:k−1,uk}: 表示控制输入的历史数据;
- m = { m 1 , m 2 … m n } m=\left\{m_{1}, m_{2} \dots m_{n}\right\} m={m1,m2…mn}: 表示所有地标的集合;
- Z 0 : k = { z 1 , z 2 , … z k } = { Z 0 : k − 1 , z k } Z_{0: k}=\left\{z_{1}, z_{2}, \ldots z_{k}\right\}=\left\{Z_{0: k-1}, z_{k}\right\} Z0:k={z1,z2,…zk}={Z0:k−1,zk}: 表示所有地标观测的集合。
2.2 SLAM问题的概率分布
P ( x k , m ∣ Z 0 : k , U 0 : k , x 0 ) P\left(x_{k}, m | Z_{0: k}, U_{0: k}, x_{0}\right) P(xk,m∣Z0:k,U0:k,x0)
表达式描述了,当给定 k k k时刻的地标观测值,控制输入值和机器人初始状态时,此时地标位置和机器人状态的联合后验概率密度。通常,SLAM问题可以递归求解。从 k − 1 k−1 k−1时刻的分布 P ( x k − 1 , m ∣ Z 0 : k − 1 , U 0 : k − 1 , x 0 ) P\left(x_{k-1}, m | Z_{0: k-1}, U_{0: k-1}, x_{0}\right) P(xk−1,m∣Z0:k−1,U0:k−1,x0)的估计值开始,根据 u k u_k uk和 z k z_k zk,使用贝叶斯定理计算 P ( x k , m ∣ Z 0 : k , U 0 : k , x 0 ) P\left(x_{k}, m | Z_{0: k}, U_{0: k}, x_{0}\right) P(xk,m∣Z0:k,U0:k,x0)。该计算要求定义状态转换(运动)模型和观测模型,分别描述控制输入和观测的影响。
-
运动模型: P ( x k ∣ x k − 1 , u k ) P\left(x_{k} | x_{k-1}, u_{k}\right) P(xk∣xk−1,uk),状态转换被假定为一个马尔科夫过程,在这个过程中,下一个状态 x k x_k xk只依赖于紧邻前一个状态 x k − 1 x_{k-1} xk−1,和应用的控制 u k u_k uk,并且独立于观测值和地图。
-
观测模型: P ( z k ∣ x k , m ) P\left(z_{k} | x_{k}, m\right) P(zk∣xk,m),描述机器人位置和地标位置已知时,观测 z k z_k zk的概率。
SLAM算法可分为以下两步:

上述公式提供了一个递归过程,用于计算联合后验分布 P ( x k , m ∣ Z 0 : k , U 0 : k , x 0 ) P\left(x_{k}, m | Z_{0: k}, U_{0: k}, x_{0}\right) P(xk,m∣Z0:k,U0:k,x0)。此递归是运动模型 P ( x k ∣ x k − 1 , u k ) P\left(x_{k} | x_{k-1}, u_{k}\right) P(xk∣xk−1,uk)和观测模型 P ( z k ∣ x k , m ) P\left(z_{k} | x_{k}, m\right) P(zk∣xk,m)的函数。
2.3 SLAM概率分布讨论
为方便讨论,将 P ( x k , m ∣ Z 0 : k , U 0 : k , x 0 ) P\left(x_{k}, m | Z_{0: k}, U_{0: k}, x_{0}\right) P(xk,m∣Z0:k,U0:k,x0)简写为 P ( x k , m ∣ z k ) P\left(x_{k}, m | z_k\right) P(xk,m∣zk)。由于观测模型 P ( z k ∣ x k , m ) P\left(z_{k} | x_k,m\right) P(zk∣xk,m)表明地标观测值和机器人和地标之间存在依赖关系,因此 P ( x k , m ∣ z k ) ≠ P ( x k ∣ z k ) P ( m ∣ z k ) P\left(x_{k}, m | z_{k}\right) \neq P\left(x_{k} | z_{k}\right) P\left(m | z_{k}\right) P(xk,m∣zk)=P(xk∣zk)P(m∣zk)。
回顾图1,地标的估计值和真实值之间存在误差,然而,这些误差是高度相关的。更重要的是,随着越来越多的观测,地标间估计值的相关性单调递增。实际上,这意味着无论机器人如何运动,对地标的相对位置的认知总是在提高(收敛),而不是发散。
三、SLAM解决方案
3.1 EKF-SLAM
- 运动模型: x k = f ( x k − 1 , u k ) + w k x_{k}=f\left(x_{k-1}, u_{k}\right)+w_{k} xk=f(xk−1,uk)+wk,其中, f ( . ) f(.) f(.)指非线性的系统状态转换函数, w k w_k wk指运动过程中的预测误差,服从 N ( 0 , Q ) N(0,Q) N(0,Q)的高斯白噪声。
- 观测模型: z k = h ( x k , m ) + v k z_{k}=h\left(x_{k}, m\right)+v_{k} zk=h(xk,m)+vk,其中, h ( . ) h(.) h(.)是非线性测量模型, v k v_k vk代表观测误差,服从 N ( 0 , R ) N(0,R) N(0,R)的高斯白噪声。

其中, ∇ f ∇f ∇f是 f ( . ) f(.) f(.)的雅可比矩阵。

其中, ∇ h ∇h ∇h是 h ( . ) h(.) h(.)的雅可比矩阵。
EKF-SLAM的缺点
- 算法的时间复杂度为 n 2 n^2 n2, n n n代表锚点的数量。
- EKF假定机器人的运动和观察存在高斯噪声。在这种情况下,传感器中的不确定性必须相对较小,因为EKF中的线性过程可能会引入无法忍受的噪声。
- EKF代表高斯后验模型,它是一种单峰分布,仅对处理后验围绕真实状态且不确定性很小的问题时才有效。
3.2 FastSLAM
FastSLAM以递归蒙特卡罗采样或粒子滤波为基础,首次直接表示了非线性过程模型和非高斯姿态分布。FastSLAM的基本结构是一个R-B状态(求最优解过程),轨迹由加权样本表示,并通过解析计算得到地图。算法基本思想是通过粒子滤波对运动状态进行递归估计,通过EKF对地图映射状态进行递归估计。
对于SLAM, R-B粒子滤波的一般形式如下。
假设在 t − 1 t-1 t−1时刻,联合状态(机器人位置姿态,观测地标位置姿态)可以用 { w k − 1 ( i ) , X 0 : k − 1 ( i ) , P ( m ∣ X 0 : k − 1 ( i ) , Z 0 : k − 1 ) } i N \left\{w_{k-1}^{(i)}, X_{0: k-1}^{(i)}, P\left(m | X_{0: k-1}^{(i)}, Z_{0: k-1}\right)\right\}_{i}^{N} {wk−1(i),X0:k−1(i),P(m∣X0:k−1(i),Z0:k−1)}iN表示,则有:
-
对于每个粒子,以特定的粒子历史为条件,计算提出的分布,并从中提取样本
x k ( i ) ∼ π ( x k ∣ X 0 : k − 1 ( i ) , Z 0 : k , u k ) \mathbf{x}_{k}^{(i)} \sim \pi\left(\mathbf{x}_{k} | \mathbf{X}_{0: k-1}^{(i)}, \mathbf{Z}_{0: k}, \mathbf{u}_{k}\right) xk(i)∼π(xk∣X0:k−1(i),Z0:k,uk) -
如果有必要,执行重采样。(什么时候重采样是一个未解决的问题。有些方案会对每个时刻重采样,有些则在固定时间间隔后取样,还有一些则在权重方差超过阈值时取样)重采样是通过从集合 { X 0 : k ( i ) } i N \left\{X_{0: k}^{(i)}\right\}_{i}^{N} {X0:k(i)}iN中选择粒子,并替换它们,包括它们的相关映射来完成的,选择的概率与 w k ( i ) w_{k}^{(i)} wk(i)成正比。选定的粒子给予均匀的权值, w k ( i ) = 1 / N w_{k}^{(i)}=1 / \mathrm{N} wk(i)=1/N。
-
对于每个粒子,用已知姿态的简单映射操作对观测到的地标进行EKF更新。
与EKF-SLAM相比,FastSLAM具有许多优势。
- FastSLAM可以在时间上以锚的数量为对数实现,与普通的EKF-SLAM相比具有计算优势。
- FastSLAM提供了显著的数据关联鲁棒性,因为它可以保持多个数据关联的后验,而不仅仅是基于EKF-SLAM中包含的增量最大似然数据关联,在任何时间点仅跟踪单个数据关联。
- FastSLAM还可以处理非线性模型,因为粒子滤波器可以处理非线性机器人运动模型,并且可以保证在某些假设下收敛。
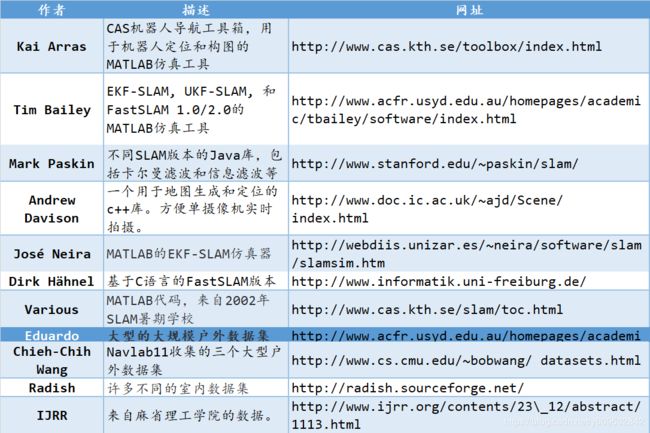
四、SLAM实现
截至2006年,SLAM领域的研究人员编写了演示SLAM的软件,分别在MATLAB、C++和Java中实现;此外,他们还提供了一些来自真实环境中传感器数据集,这是评估各种SLAM算法的宝贵资源。具体内容见下表。