30. 串联所有单词的子串
解法一
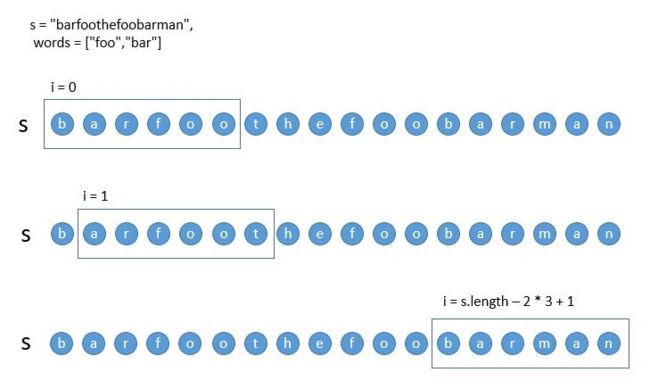
首先,最直接的思路,判断每个子串是否符合,符合就把下标保存起来,最后返回即可。
如上图,利用循环变量 i ,依次后移,判断每个子串是否符合即可。
怎么判断子串是否符合?这也是这个题的难点了,由于子串包含的单词顺序并不需要固定,如果是两个单词 A,B,我们只需要判断子串是否是 AB 或者 BA 即可。如果是三个单词 A,B,C 也还好,只需要判断子串是否是 ABC,或者 ACB,BAC,BCA,CAB,CBA 就可以了,但如果更多单词呢?那就崩溃了。
用两个 HashMap 来解决。首先,我们把所有的单词存到 HashMap 里,key 直接存单词,value 存单词出现的个数(因为给出的单词可能会有重复的,所以可能是 1 或 2 或者其他)。然后扫描子串的单词,如果当前扫描的单词在之前的 HashMap 中,就把该单词存到新的 HashMap 中,并判断新的 HashMap 中该单词的 value 是不是大于之前的 HashMap 该单词的 value ,如果大了,就代表该子串不是我们要找的,接着判断下一个子串就可以了。如果不大于,那么我们接着判断下一个单词的情况。子串扫描结束,如果子串的全部单词都符合,那么该子串就是我们找的其中一个。看下具体的例子。
看下图,我们把 words 存到一个 HashMap 中。
然后遍历子串的每个单词。
第一个单词在 HashMap1 中,然后我们把 foo 存到 HashMap2 中。并且比较此时 foo 的 value 和 HashMap1 中 foo 的 value,1 < 2,所以我们继续扫描。
第二个单词也在 HashMap1 中,然后把 foo 存到 HashMap2 中,因为之前已经存过了,所以更新它的 value 为 2 ,然后继续比较此时 foo 的 value 和 HashMap1 中 foo 的 value,2 <= 2,所以继续扫描下一个单词。
第三个单词也在 HashMap1 中,然后把 foo 存到 HashMap2 中,因为之前已经存过了,所以更新它的 value 为 3,然后继续比较此时 foo 的 value 和 HashMap1 中 foo 的 value,3 > 2,所以表明该字符串不符合。然后判断下个子串就好了。
当然上边的情况都是单词在 HashMap1 中,如果不在的话就更好说了,不在就表明当前子串肯定不符合了,直接判断下个子串就好了。
看一下代码吧
public List findSubstring(String s, String[] words) {
List res = new ArrayList();
int wordNum = words.length;
if (wordNum == 0) {
return res;
}
int wordLen = words[0].length();
//HashMap1 存所有单词
HashMap allWords = new HashMap();
for (String w : words) {
int value = allWords.getOrDefault(w, 0);
allWords.put(w, value + 1);
}
//遍历所有子串
for (int i = 0; i < s.length() - wordNum * wordLen + 1; i++) {
//HashMap2 存当前扫描的字符串含有的单词
HashMap hasWords = new HashMap();
int num = 0;
//判断该子串是否符合
while (num < wordNum) {
String word = s.substring(i + num * wordLen, i + (num + 1) * wordLen);
//判断该单词在 HashMap1 中
if (allWords.containsKey(word)) {
int value = hasWords.getOrDefault(word, 0);
hasWords.put(word, value + 1);
//判断当前单词的 value 和 HashMap1 中该单词的 value
if (hasWords.get(word) > allWords.get(word)) {
break;
}
} else {
break;
}
num++;
}
//判断是不是所有的单词都符合条件
if (num == wordNum) {
res.add(i);
}
}
return res;
}
时间复杂度:假设 s 的长度是 n,words 里有 m 个单词,那么时间复杂度就是 O(n * m)。
空间复杂度:两个 HashMap,假设 words 里有 m 个单词,就是 O(m)。
解法二
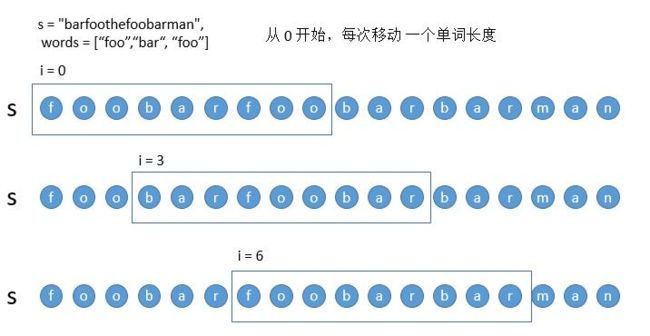
我们在解法一中,每次移动一个字符。
现在为了方便讨论,我们每次移动一个单词的长度,也就是 3 个字符,这样所有的移动被分成了三类。
以上三类我们以第一类从 0 开始移动为例,讲一下如何对算法进行优化,有三种需要优化的情况。
情况一:当子串完全匹配,移动到下一个子串的时候。

在解法一中,对于 i = 3 的子串,我们肯定是从第一个 foo 开始判断。但其实前两个 foo 都不用判断了 ,因为在判断上一个 i = 0 的子串的时候我们已经判断过了。所以解法一中的 HashMap2 每次并不需要清空从 0 开始,而是可以只移除之前 i = 0 子串的第一个单词 bar 即可,然后直接从箭头所指的 foo 开始就可以了。
情况二:当判断过程中,出现不符合的单词。

但判断 i = 0 的子串的时候,出现了 the ,并不在所给的单词中。所以此时 i = 3,i = 6 的子串,我们其实并不需要判断了。我们直接判断 i = 9 的情况就可以了。
情况三:判断过程中,出现的是符合的单词,但是次数超了。

对于 i = 0 的子串,此时判断的 bar 其实是在 words 中的,但是之前已经出现了一次 bar,所以 i = 0 的子串是不符合要求的。此时我们只需要往后移动窗口,i = 3 的子串将 foo 移除,此时子串中一定还是有两个 bar,所以该子串也一定不符合。接着往后移动,当之前的 bar 被移除后,此时 i = 6 的子串,就可以接着按正常的方法判断了。
所以对于出现 i = 0 的子串的情况,我们可以直接从 HashMap2 中依次移除单词,当移除了之前次数超的单词的时候,我们就可以正常判断了,直接从移除了超出了次数的单词后,也就是 i = 6 开始判断就可以了。
看一下代码吧。
public List findSubstring(String s, String[] words) {
List res = new ArrayList();
int wordNum = words.length;
if (wordNum == 0) {
return res;
}
int wordLen = words[0].length();
HashMap allWords = new HashMap();
for (String w : words) {
int value = allWords.getOrDefault(w, 0);
allWords.put(w, value + 1);
}
//将所有移动分成 wordLen 类情况
for (int j = 0; j < wordLen; j++) {
HashMap hasWords = new HashMap();
int num = 0; //记录当前 HashMap2(这里的 hasWords 变量)中有多少个单词
//每次移动一个单词长度
for (int i = j; i < s.length() - wordNum * wordLen + 1; i = i + wordLen) {
boolean hasRemoved = false; //防止情况三移除后,情况一继续移除
while (num < wordNum) {
String word = s.substring(i + num * wordLen, i + (num + 1) * wordLen);
if (allWords.containsKey(word)) {
int value = hasWords.getOrDefault(word, 0);
hasWords.put(word, value + 1);
//出现情况三,遇到了符合的单词,但是次数超了
if (hasWords.get(word) > allWords.get(word)) {
// hasWords.put(word, value);
hasRemoved = true;
int removeNum = 0;
//一直移除单词,直到次数符合了
while (hasWords.get(word) > allWords.get(word)) {
String firstWord = s.substring(i + removeNum * wordLen, i + (removeNum + 1) * wordLen);
int v = hasWords.get(firstWord);
hasWords.put(firstWord, v - 1);
removeNum++;
}
num = num - removeNum + 1; //加 1 是因为我们把当前单词加入到了 HashMap 2 中
i = i + (removeNum - 1) * wordLen; //这里依旧是考虑到了最外层的 for 循环,看情况二的解释
break;
}
//出现情况二,遇到了不匹配的单词,直接将 i 移动到该单词的后边(但其实这里
//只是移动到了出现问题单词的地方,因为最外层有 for 循环, i 还会移动一个单词
//然后刚好就移动到了单词后边)
} else {
hasWords.clear();
i = i + num * wordLen;
num = 0;
break;
}
num++;
}
if (num == wordNum) {
res.add(i);
}
//出现情况一,子串完全匹配,我们将上一个子串的第一个单词从 HashMap2 中移除
if (num > 0 && !hasRemoved) {
String firstWord = s.substring(i, i + wordLen);
int v = hasWords.get(firstWord);
hasWords.put(firstWord, v - 1);
num = num - 1;
}
}
}
return res;
}
时间复杂度:算法中外层的两个for 循环的次数肯定是所有的子串,假设是 n。考虑一下,最极端的情况,每个子串的判断都进了 while 循环,wordNum 等于 m。对于解法一,因为每次都是从头判断,所以 while 循环循环了 m 次。但这里我们由于没有清空,所以每次只判断新加入的单词就可以了,只需判断一次,所以时间复杂度是 O(n)。
或者换一种理解方式,判断子串是否符合,本质上也就是判断每个单词符不符合,假设 s 的长度是 n,那么就会大约有 n 个子串,也就是会有 n 个单词。而对于每个单词,我们只有刚开始判断符不符合的时候访问一次,还有就是把它移除的时候访问一次,所以每个单词最多访问 2 次,所以时间复杂度是 O(n)。
空间复杂度:没有变化,依旧是两个 HashMap, 假设 words 里有 m 个单词,就是 O(m)。
总
这道题最大的亮点就是应用了 HashMap 了吧,使得我们不再纠结于子串包含单词的顺序。然后对于算法的优化上,还是老思