在kaggle上的Digit Recognizer(MNIST)比赛中用Tensorflow实现多层神经网络算法

前言

在kaggle竞赛中，有不少给大家练习的入门级别的比赛，分别是：

• Titanic: Machine Learning from Disaster
• House Prices: Advanced Regression Techniques
• Digit Recognizer
  其中，Titanic是适合机器学习以及神经网络入门的比赛；House Prices是适合练习特征提取的比赛，因为其特征种类繁多；Digit Recognizer使用的是MNIST数据集，是一个在科研界都被广泛使用的数据集，其由Yann LeCun, Courant Institute, NYU、Corinna Cortes, Google Labs, New York和Christopher J.C. Burges, Microsoft Research, Redmond共同维护，该数据集比较适合用来练习卷积神经网络以及其它各种神经网络，官网网址为：MNIST官网，上面有不同文章不同算法得到的对于MNIST的最优的结果。kaggle上该比赛的超链接为：Digit Recognizer

若想看在MNIST数据集上用Tensorflow实现多层神经网络算法，请点击右侧超链接：请点我。

由于kaggle未使用所有的原始的MNIST测试集来测试准确率，因此需要自行提交预测结果进入kaggle的服务器以获得最终的准确率，在kaggle上，每天能提交5次，本博客主要分为两部分：

1. 用于调试参数的代码；
2. 用于提交结果的代码。

需要下载的东西（数据和代码）

训练集、测试集以及相关代码都在如下的百度云盘中：

链接：https://pan.baidu.com/s/1YL1VjJUqPp_vBEGo4HQWWQ 
提取码：frjr 

用于调试参数的代码讲解

首先需要先导入一些库

# 数据分析库
import pandas as pd
# 科学计算库
import numpy as np 
# 导入tensorflow
import tensorflow as tf

import matplotlib.pyplot as plt

from tensorflow.python.framework import ops

然后导入数据集(在上方的百度网盘中可以下载)

data_train = pd.read_csv("train.csv")
data_test = pd.read_csv("test.csv")

通常来说，若是第一次遇见这些数据集，应该先简略的看看其中的数据的详情

data_train.head()

运行上述代码后，会出现

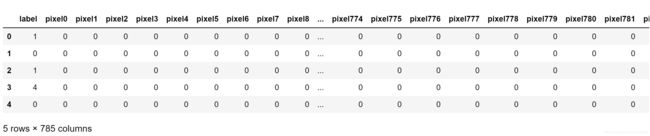
该代码的意思是查看data_train的前五行数据，可以发现，第一列是label，即该行是什么数字，后面pixel0到pixel783为[0,255]的像素值，每一张数字图片都是$28\times 28$的尺寸，此处是将其拉长一行向量，因此有$28\times 28=784$个元素。

接下来

data_train.info()

运行后出现以下结果：

由上可知，训练集共有42000组数据，每组数据都是一张图片，每组数据都有785列，其中第一列为label，剩下的784列则由图片拉成向量组成。

虽然改代码不使用训练集，但还是顺便输出出来看一下

data_test.head()

结果如下：

可以轻松的发现，测试集理所当然的少了label，因为在提交结果时就是要来预测测试集中的label。

接下来看一下测试集的属性

data_test.info()

结果如下：

其中，测试集只有28000组数据，少于训练集的42000组。测试集只有784列，因为没有label。

还原前几张图片出来看看（前5张）

for i in np.arange(5):
    num=data_train.iloc[i]
    pic=np.array(num)
    pic=pic[1:785]
    pic=pic.reshape(28,28)
    plt.title(str(num.label)) 
    plt.imshow(pic,cmap="gray")
    plt.show()

结果如下：





对照之前输出的训练集的前5行数据的label可以发现这5张图片确实对应的是数字1、0、1、4、0。

接下来需要去掉标签特征的相关性，将标签进行独热编码，因为例如数字1和数字5是没有谁优谁劣的，如果直接用1和5来作为标签，则会误导计算机数字5比数字1要好\坏5倍的潜在含义。

label_dummies = pd.get_dummies(data_train['label'])
data_train = data_train.join(label_dummies)

接下来再看一下数据集当前是什么样的

data_train.head()

结果如下所示：

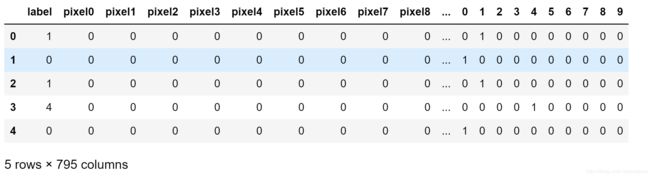
可以发现，在训练集中的最后10列增加了10个特征，此时这10个特征中1位于10个特征中的第几列，那该行数据的label就是几。

使用神经网络算法进行训练,此处设计简单的双层神经网络

# 初始化一个 Session
ops.reset_default_graph()
sess = tf.Session()

# 调参时固定随机种子
seed = 1
tf.set_random_seed(seed)
np.random.seed(seed) 

分割数据集来调试参数

predictors=data_train.columns.values.tolist()[1:785]
x_vals=data_train[predictors]
label_dum=data_train.columns.values.tolist()[785:]
y_vals=data_train[label_dum]
# 分割训练集 train/test = 80%/20%
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))
x_vals_train = x_vals.loc[train_indices]
x_vals_test = x_vals.loc[test_indices]
y_vals_train = y_vals.loc[train_indices]
y_vals_test = y_vals.loc[test_indices]

# 定义变量函数 (weights and bias)
def init_weight(shape, st_dev):
    weight = tf.Variable(tf.truncated_normal(shape, stddev=st_dev))
    return(weight)
    
def init_bias(shape, st_dev):
    bias = tf.Variable(tf.truncated_normal(shape, stddev=st_dev))
    return(bias)
    
# 创建占位符(Placeholders)
x_data = tf.placeholder(shape=[None, len(predictors)], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 10], dtype=tf.float32)

构建双层神经网络

# 创建不同的层:
def relu_layer(input_layer, weights, biases):
    layer = tf.add(tf.matmul(input_layer, weights), biases)
    return(tf.nn.relu(layer))

def liner_layer(input_layer, weights, biases):
    layer = tf.add(tf.matmul(input_layer, weights), biases)
    return(layer)

rand_st_dev=0.01
#-------- 创建第一个隐藏层 (100个隐藏单元)--------
hidden_nodes1=100
weight_1 = init_weight(shape=[len(predictors), hidden_nodes1], st_dev=rand_st_dev)
bias_1 = init_bias(shape=[hidden_nodes1], st_dev=rand_st_dev)
layer_1 = relu_layer(x_data, weight_1, bias_1)

#-------- 创建输出层 (10个输出)--------
output_nodes=10
weight_output = init_weight(shape=[hidden_nodes1, output_nodes], st_dev=rand_st_dev)
bias_output = init_bias(shape=[output_nodes], st_dev=rand_st_dev)
final_output = liner_layer(layer_1, weight_output, bias_output)

# 声明损失函数 (softmax)
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=final_output, labels=y_target))

# 声明优化算法(optimizer)
my_opt = tf.train.RMSPropOptimizer(0.0001,0.9)
train_step = my_opt.minimize(loss)

在此处声明计算准确率的op

predictions=tf.placeholder(shape=[None,10], dtype=tf.int32)
train_correct_prediction = tf.equal(tf.argmax(y_vals_train,1),
                                    tf.argmax(predictions,1))
train_accuracy_op = tf.reduce_mean(tf.cast(train_correct_prediction, tf.float32))
test_correct_prediction = tf.equal(tf.argmax(y_vals_test,1),
                                    tf.argmax(predictions,1))
test_accuracy_op = tf.reduce_mean(tf.cast(test_correct_prediction, tf.float32))

用训练集和验证集来调参

# 声明批量大小(batch size)
batch_size = 512
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)

# 训练循环
loss_vec = []
test_loss = []
train_acc=[]
test_acc=[]

for i in range(2000):
    rand_index = np.random.choice(len(x_vals_train), size=batch_size)
    rand_x = x_vals_train.iloc[rand_index]
    rand_y = y_vals_train.iloc[rand_index]
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
   
    if (i+1)%50==0:
        temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
        loss_vec.append(np.sqrt(temp_loss))

        predictions_train=sess.run(final_output,feed_dict={x_data: x_vals_train})
        train_accuracy=sess.run(train_accuracy_op,feed_dict={predictions:predictions_train})
        train_acc.append(train_accuracy)
        
        
        test_temp_loss = sess.run(loss, feed_dict={x_data: x_vals_test,y_target:y_vals_test})
        test_loss.append(np.sqrt(test_temp_loss))
        
        predictions_test=sess.run(final_output,feed_dict={x_data: x_vals_test})
        test_accuracy=sess.run(test_accuracy_op,feed_dict={predictions:predictions_test})
        test_acc.append(test_accuracy)
        
        print('迭代次数: ' + str(i+1) + '. 训练损失 = ' + str(temp_loss)+ '. 测试损失 = ' + str(test_temp_loss))
        print("训练集准确率为: " + str(train_accuracy) + " . 测试集准确率为: " + str(test_accuracy))
        print(" ")

此处的结果为：

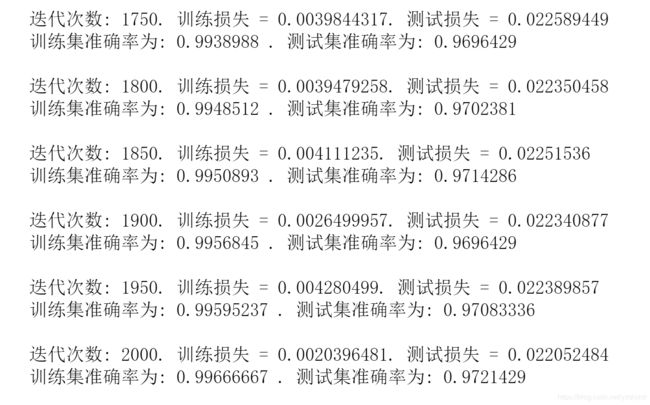
此处由于输出太多，故只截取最后的部分以作参考，由上可知，在训练了2000次后，训练集的准确率为0.99666667，已十分接近于1，而测试集的准确率为0.9721429，也是挺高的了。因为这个网络太简单了，因此限制了模型的泛化能力，所以参数没有花太多时间去调整，相信如果进一步调参，该网络的性能会更好。

最后绘制一些图来看看算法的性能趋势，其中每迭代50次画一个点，这是由于如果每次迭代都计算这些东西的话成本过高。

# 绘制 loss (MSE)
plt.plot(loss_vec, 'k-', label='Train Loss')
plt.plot(test_loss, 'r--', label='Test Loss')
plt.title('Loss (MSE) per Generation')
plt.legend(loc='upper right')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()

# 绘制 train 和 test 的准确率
plt.plot(train_acc, 'k-', label='Train Set Accuracy')
plt.plot(test_acc, 'r--', label='Test Set Accuracy')
plt.title('Train and Test Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()

输出结果如下所示：


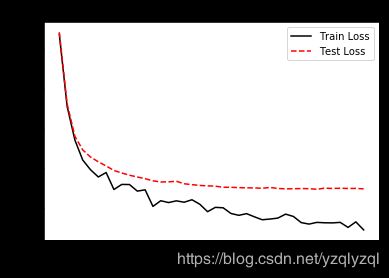
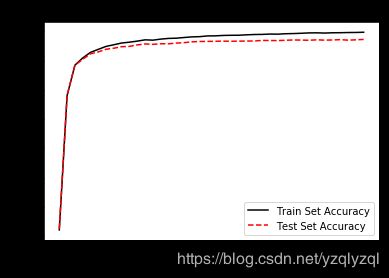
由上可知，验证集损失一直在下降，但没有训练集损失下降得快，且由于是小批量训练，训练集损失的下降呈现锯齿状，而验证集损失的下降趋势比较光滑。
验证集准确率一直在上升，但没有训练集准确率上升得快。

最后是一个好习惯，手动的关闭当前的session

sess.close()

至此，用于调试参数的代码讲解结束，完整的代码请参照开头百度云盘中的MNIST_base_update_parameters.ipynb或MNIST_base_update_parameters.py。

用于提交结果的代码讲解

通常来说，用于提交结果的代码是用用于调试参数的代码来修改得来的，这样比较方便且会减少未知bug的发生。此时使用调好的参数和所有训练数据来训练网络。

首先，依然是先导入所需的库

# 数据分析库
import pandas as pd
# 科学计算库
import numpy as np 
# 导入tensorflow
import tensorflow as tf

import matplotlib.pyplot as plt

from tensorflow.python.framework import ops

然后导入训练集合测试集

data_train = pd.read_csv("train.csv")
data_test = pd.read_csv("test.csv")

去掉训练集标签（label）特征的相关性

label_dummies = pd.get_dummies(data_train['label'])
data_train = data_train.join(label_dummies)

使用神经网络算法进行训练,此处按简单的双层神经网络的结构来设计网络

# 初始化一个 Session
ops.reset_default_graph()
sess = tf.Session()

# 调参时固定随机种子
seed = 1
tf.set_random_seed(seed)
np.random.seed(seed) 

划分训练集的特征x和标签y以及测试集的特征

predictors=data_train.columns.values.tolist()[1:785]
x_train=data_train[predictors]
label_dum=data_train.columns.values.tolist()[785:]
y_train=data_train[label_dum]

x_test=data_test[predictors]

加下来定义权重和偏置的函数，同时声明占位符

# 定义变量函数 (weights and bias)
def init_weight(shape, st_dev):
    weight = tf.Variable(tf.random_normal(shape, stddev=st_dev))
    return(weight)
    

def init_bias(shape, st_dev):
    bias = tf.Variable(tf.random_normal(shape, stddev=st_dev))
    return(bias)
    
    
# 声明占位符（Placeholders）
x_data = tf.placeholder(shape=[None, len(predictors)], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 10], dtype=tf.float32)

构建双层神经网络

# 创建不同的层:
def relu_layer(input_layer, weights, biases):
    layer = tf.add(tf.matmul(input_layer, weights), biases)
    return(tf.nn.relu(layer))

def sigmoid_layer(input_layer, weights, biases):
    layer = tf.add(tf.matmul(input_layer, weights), biases)
    return(tf.nn.sigmoid(layer))

def liner_layer(input_layer, weights, biases):
    layer = tf.add(tf.matmul(input_layer, weights), biases)
    return(layer)

rand_st_dev=0.01
#-------- 创建第一个隐藏层 (100个隐藏单元)--------
hidden_nodes1=100
weight_1 = init_weight(shape=[len(predictors), hidden_nodes1], st_dev=rand_st_dev)
bias_1 = init_bias(shape=[hidden_nodes1], st_dev=rand_st_dev)
layer_1 = relu_layer(x_data, weight_1, bias_1)

#-------- 创建输出层 (10个输出)--------
output_nodes=10
weight_output = init_weight(shape=[hidden_nodes1, output_nodes], st_dev=rand_st_dev)
bias_output = init_bias(shape=[output_nodes], st_dev=rand_st_dev)
final_output = liner_layer(layer_1, weight_output, bias_output)

# 声明损失函数 (softmax)
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=final_output, labels=y_target))

# 声明优化算法(optimizer)
my_opt = tf.train.RMSPropOptimizer(0.0001,0.9)
train_step = my_opt.minimize(loss)

在此处声明计算准确率的op

predictions=tf.placeholder(shape=[None,10], dtype=tf.int32)
train_correct_prediction = tf.equal(tf.argmax(y_train,1),
                                    tf.argmax(predictions,1))
train_accuracy_op = tf.reduce_mean(tf.cast(train_correct_prediction, tf.float32))

训练网络

# 声明批量大小(batch size)
batch_size = 512
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)

# 训练循环
loss_vec = []
train_acc=[]

for i in range(2000):
    rand_index = np.random.choice(len(x_train), size=batch_size)
    rand_x = x_train.iloc[rand_index]
    rand_y = y_train.iloc[rand_index]
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
    
    if (i+1)%100==0:
        temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
        loss_vec.append(np.sqrt(temp_loss))
        
        predictions_train=sess.run(final_output,feed_dict={x_data: x_train})
        train_accuracy=sess.run(train_accuracy_op,feed_dict={predictions:predictions_train})
        train_acc.append(train_accuracy)
        
        print('迭代次数: ' + str(i+1) + '. 训练损失 = ' + str(temp_loss))
        print("训练集准确率为: " + str(train_accuracy))
        print(" ")

输出如下所示，在此仅截取最后的一部分输出：

然后，绘制趋势图来观测一下结果

# 绘制 loss (MSE)
plt.plot(loss_vec, 'k-', label='Train Loss')
plt.title('Loss (MSE) per Generation')
plt.legend(loc='upper right')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()

# 绘制 train 和 test 的准确率
plt.plot(train_acc, 'k-', label='Train Set Accuracy')
plt.title('Train and Test Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()

输出如下所示：


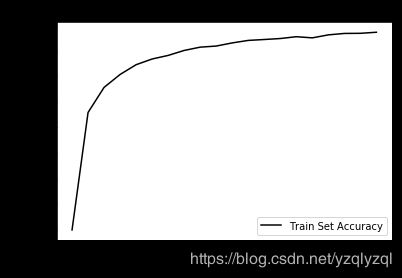
最后生成所要提交的文档，文档名为“20190725_1.csv”：

data_test_predictions=sess.run(final_output,feed_dict={x_data: x_test})
predictions=sess.run(tf.argmax(data_test_predictions,1))
Submission = pd.DataFrame({'ImageId':np.arange(1,28001),'Label':predictions})
Submission.to_csv('20190725_1.csv',index=False,sep=',')

然后是好习惯

sess.close()

手动关闭session。

提交后的结果

将20190725_1.csv在kaggle上提交后可得：

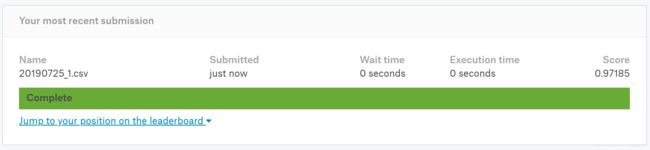
此处正确率有$97.185\%$，对于这种简单的模型来说已经是非常不错的准确率了，当然在此处还能通过调参来进一步提高准确率。
当然，和现在MNIST官网上最优的结果还相差甚远，

但那是之后更复杂模型的事了，该结果的错误率仅为$0.23\%$，即正确率为$99.77\%$。