随机森林算法的总结和基于python的简单实现
第一次写博客,水平有限,恳请指正交流.
接触机器学习也有一段时间了,以前只是看看理论,调调sklearn的包,感觉并没有真正的明白算法的具体细节。
现在开始利用空闲时间,把自己学过的算法用python实现一下,代码学习时间很短,所以代码结构不是很好,也没优化,以后我会努力写出优秀的代码的。
一 前言:随机森林(Random Forests)真正被系统性的提出是 BREIMAN 2001年的论文。
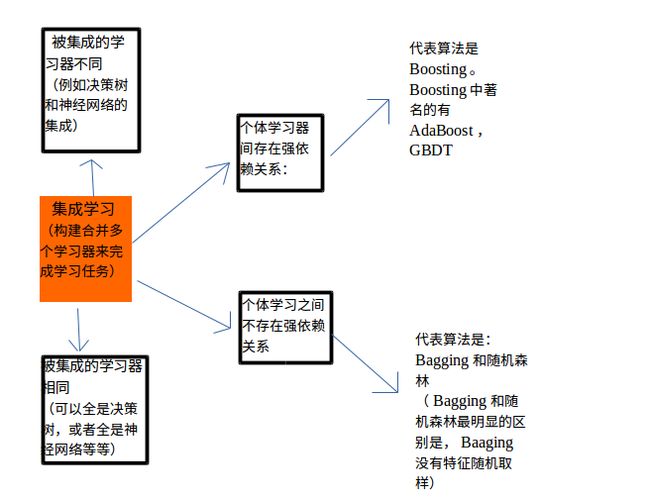
1 随机森林与集成学习的关系:
说到随机森林,就不得不提一下机器学习中的集成学习方法。这里参考周志华老师的西瓜书简单总结一下集成学习。
2.随机森林与决策树的关系
二.随机森林特点:
1.随机性:随机体现在两个方面,生成单颗决策树时,需要进行样本的有放回抽样(自助采样法),
在生成单颗决策树时,每个结点处,进行特征的随机抽样。
2.out-of-bag估计:每颗决策树的生成都需要自助采样,这时就会有1/3的数据未被选中,这部分数据称为袋外数据。
可以根据这部分数据进行 森林泛化误差(BREIMAN论文中介绍说袋外估计的泛化误差近似==测试集大小和训练集大小相同时的测试误差)特征重要性的估计。在代码中实现了泛化误差的估计,特征重要性有时间再补上。
(特征重要性的估计通常有两种方法:一是使用uniform或者gaussian抽取随机值替换原特征;一是通过permutation的方式将原来的所有N个样本的第i个特征值重新打乱分布。,第二种方法更加科学,保证了特征替代值与原特征的分布是近似的。这种方法叫做permutation test,即在计算第i个特征的重要性的时候,将N个样本的第i个特征重新洗牌,然后比较D和D(p)表现的差异性。如果差异很大,则表明第i个特征是重要的。)
3.随机森林未用到决策树的剪枝,那怎样控制模型的过拟合呢?主要通过控制 树的深度(max_depth),结点停止分裂的最小样本数(min_size)等参数。
4.缺失值处理:缺失值可以分为出现在训练集中,出现在测试集中两种情况。(本文代码只实现了测试集中缺失值的自动处理)
决策树(C4.5,CART等)具有缺失值自动处理能力。西瓜书中介绍了C4.5的缺失值处理原理。我对随机森林中的缺失值处理机制没有深究(个人理解:缺失值的处理需要针对不同的数据集和测试结果进行相应调整)。BREIMAN随机森林的网站上介绍的缺失值处理过程有很多种,这里写一下最简单的处理方式:
训练集中数据缺失:若样本缺失值为非类别型属性值,则取样本所属J class中该属性未缺失值的中值。若为类别型属性值缺失,则从样本所属J class中选择该属性最常出现的类别进行填充。(直白点说就是对于未知的东西就把它判断为大众化的,虽然不是很精确,但是可以在有限的计算复杂度下尽量降低风险)
测试集中数据缺失:When there is a test set, there are two different methods of replacement depending on whether labels exist for the test set.If they do, then the fills derived from the training set are used as replacements. If labels no not exist, then each case in the test set is replicated nclass times (nclass= number of classes). The first replicate of a case is assumed to be class 1 and the class one fills used to replace missing values. The 2nd replicate is assumed class 2 and the class 2 fills used on it.This augmented test set is run down the tree. In each set of replicates, the one receiving the most votes determines the class of the original case.(网站原文)
5.随机森林重要的参数:
n_features:推荐值为特征数量的平方根
n_trees: 森林中的树按说越多越好,但是当数量多到一定程度时,精度的提升已经不明显,但是计算消耗却很大。
评价函数:可以为Gini_index,信息增益,平方误差损失,方差等等,当然可以根据数据集类型的不同自己选择合适的评价函数(具体情况具体分析)
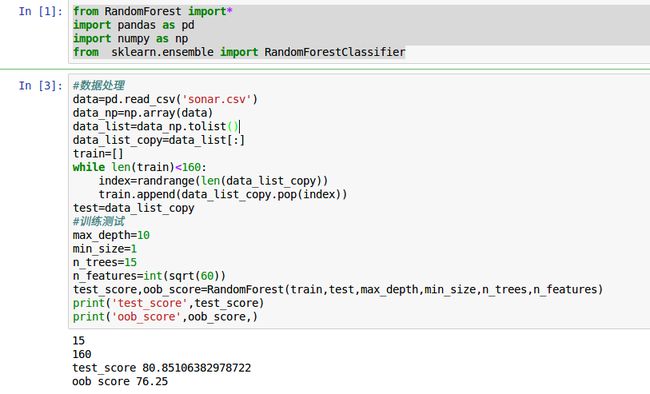
三 .代码
1.代码思想很简单,主要部分在于决策树的构建,可以参考《集体智慧编程》或者是MIT计算机科学和python或者是算法导论中的tree相关知识。
决策树的构建主要依据递归思想,并把每个结点当成一个实例。下面上代码:
# -*- coding:utf-8 -*-
'''
几点需要注意的问题
1:随机森林的随机体现在两个方面:样本有放回随机采样(西瓜书中的bootstrap),产生独立同分布子集(代码中用的randrange),
特征值采样(每个结点都采一次样,而不是一颗树采一次);
2:当train中存在缺失值,c4.5是按权重分配
当test中存在缺失值,在某结点走向两个分叉tb,fb,并根据tbfb的样本比重,对返回到该结点的结果进行重新计算
4:输出为label或者是概率(叶结点不纯时可疑选择输出概率)
7:随机森林中正则化:首先正则化是为了降低过拟合。对于决策树,降低过拟合的手段包括:剪枝,控制tree深度,控制gain或者gini变化大小,
以及控制结点样本数等情况,随机森林中没有剪枝操作,但是有max_depth,min_size等进行控制
8:当从原始训练集(size=m)进行有放回采样时(子集大小m,采样率1),会有1/3的数据未被取到。
5:特征的重要性程度,通过out-of-bag 估计
6:分类问题 (回归问题待实现)
'''
from random import randrange
from math import sqrt, log2
from drawtree import *
############################################################
########################一些数据处理函数的实现:#################
def subsample(dataset):
'''样本有放回随机采样,输入数据集,返回采样子集'''
sample=list()
n_sample=len(dataset)
while len(sample)=value
else:
split_fun = lambda row: row[column] == value
#将数据集拆分成两个集合并返回
set1=[row for row in rows if split_fun(row)]
set2=[row for row in rows if not split_fun(row)]
return (set1,set2)
#对各种可能的结果进行计数(每一行数据的最后一列(标签)记录了这一结果)
def uniquecounts(rows):
'''rows:输入样本集合;
返回值dict'''
results={}
#print(rows)
for row in rows:
rs=row[-1]
#print(rs)
if not rs in results.keys():
results[rs]=0
results[rs]+=1
return results
#决策树的构造过程:决策树构造过程中需要注意特征抽样.
def buildDTree(rows,scoref,n_features,min_size,max_depth,depth): #函数是对每个结点的建立
'''rows:数据集
scoref:评价函数
n_features:抽样特征数
min_size:结点停止继续分叉的样本数
max_depth:树的最大深度'''
if len(rows)<=min_size:
return decisionNode(results=uniquecounts(rows)) #当结点样本数量<=min_size时,停止分叉,并返回该结点的类别
if depth>=max_depth:
return decisionNode(results=uniquecounts(rows)) #当树深度>=max_depth时,停止分叉,并返回该结点的类别
current_score=scoref(rows)
#定义一些变量以记录最佳拆分条件
best_gain=0
best_criteria=None #最佳拆分点:(特征,特征取值)
best_sets=None #最佳拆分点产生的子集
#特征抽样:
rows_copy=rows[:]
features_index=[]
while len(features_index) 0:
for value in values:
(set1, set2) = divideset(data, col, value)
# 计算拆分下的信息增益:
p_set1 = float(len(set1) / len(data))
gain_sub = current_score - p_set1 * scoref(set1) - (1 - p_set1) * scoref(set2)
gain=p*gain_sub
if gain > best_gain and len(set1) > 0 and len(set2) > 0:
best_gain = gain
best_criteria = (col, value)
best_sets = (set1, set2)
else: #属性值未缺失时
for value in values:
(set1,set2)=divideset(rows,col,value)
#计算拆分下的信息增益:
p_set1=float(len(set1)/len(rows))
gain=current_score-p_set1*scoref(set1)-(1-p_set1)*scoref(set2)
if gain>best_gain and len(set1)>0 and len(set2)>0:
best_gain=gain
best_criteria=(col,value)
best_sets=(set1,set2)
#创建分支:
if best_gain>0:
TrueBranch=buildDTree(best_sets[0],scoref,n_features,min_size,max_depth,depth+1)
FalseBranch=buildDTree(best_sets[1],scoref,n_features,min_size,max_depth,depth+1)
return decisionNode(col=best_criteria[0],value=best_criteria[1],tb=TrueBranch,fb=FalseBranch)
else:
return decisionNode(results=uniquecounts(rows))
# 预测函数:
def predict_results(observation,tree):
if tree.results != None:
return tree.results
else:
v = observation[tree.col]
if v == None:
tr, fr = predict_results(observation,tree.tb), predict_results(observation,tree.fb)
tcount=sum(tr.values())
fcount=sum(fr.values())
tw=float(tcount)/(tcount+fcount)
fw=float(fcount)/(tcount+fcount)
result={}
for k,v in tr.items():
result[k]=v*tw
for k,v in fr.items():
if k not in result:result[k]=0
result[k] += v*fw
return result
else:
Branch = None
if isinstance(v, int) or isinstance(v, float):
if v >= tree.value:
Branch = tree.tb
else:
Branch = tree.fb
else:
if v == tree.value:
Branch = tree.tb
else:
Branch = tree.fb
return predict_results(observation, Branch)
def predict(observation, tree):
results=predict_results(observation,tree)
label = None
b_count = 0
for key in results.keys():
if results[key] > b_count:
b_count = results[key]
label = key
return label
##############################################################
############***精度评价函数***###########################
def accuracy(actual,predicted):
'''输入:实际值,预测值'''
correct=0
for i in range(len(actual)):
if actual[i]==predicted[i]:
correct+=1
accuracy=(float(correct)/len(actual))*100
return accuracy
##############################################################
##############***Out-of-Bag***################################
#进行袋外估计等相关函数的实现,需要注意并不是每个样本都可能出现在随机森林的袋外数据中
#因此进行oob估计时需要注意估计样本的数量
#Breiman 的论文说明 oob估计的error近似于测试集和训练集样本大小相同时的测试error
def OOB(oobdata,train,trees):
'''输入为:袋外数据dict,训练集,tree_list
return oob准确率'''
n_rows=[]
count=0
n_trees=len(trees) #森林中树的棵树
for key,item in oobdata.items():
n_rows.append(item)
print(len(n_rows)) #所有trees中的oob数据的合集
n_rows_list=sum(n_rows,[])
unique_list=[]
for l1 in n_rows_list: #从oob合集中计算独立样本数量
if l1 not in unique_list:
unique_list.append(l1)
n=len(unique_list)
print(n)
#对训练集中的每个数据,进行遍历,寻找其作为oob数据时的所有trees,并进行多数投票
for row in train:
pre = []
for i in range(n_trees):
if row not in oobdata[i]:
pre.append(predict(row,trees[i]))
if len(pre)>0:
label=max(set(pre),key=pre.count)
if label==row[-1]:
count+=1
return (float(count)/n)*100
##############################################################
############***RandomForest的实现***###########################
#综合多颗树的预测结果,给出预测结果
def bagging_predict(trees,row):
predictions=[predict(row,tree) for tree in trees]
#print(predictions)
return max(set(predictions),key=predictions.count)
def RandomForest(train,test,max_depth,min_size,n_trees,n_features,scoref=giniIndex):
trees=[] #产生的单颗树存于列表中
oobs={}
for i in range(n_trees):
subset=subsample(train)
oobs[i]=subset
tree=buildDTree(subset,scoref,n_features,min_size,max_depth,0)
trees.append(tree)
#drawtree(tree,jpeg='%d'%i)
oob_score=OOB(oobs,train,trees) #oob准确率
predictions=[bagging_predict(trees,row) for row in test]
actual = [row[-1] for row in test]
test_score=accuracy(actual, predictions) #测试集准确率
return test_score ,oob_score
贴其中一颗树的图:(这颗树的生成嗯时控制了min_size=4,所以会有不纯的叶结点)
(这棵树min_size=1,所以叶结点都很纯)
四.一些还没完成的问题:
1.随机森林进行回归分析
2.袋外估计特征重要性
3.样本权重不平衡(此次代码中假设样本权重均为1)
4.概率输出(此代码中只是根据叶结点样本统计,输出占比最大的样本的label),有时间应该实验一下label的概率输出(叶结点样本不纯时,计算各类的比例)。
参考资料:
[1]L Breiman. Random Forest[J]. Machine Learning, 2001, 45:5-32.
[2]《集体智慧编程》
[3] 西瓜书