方向余弦矩阵DCM&刚体的矢量—矩阵描述
方向余弦矩阵DCM&刚体的矢量—矩阵描述
- 简介
- 方向余弦矩阵
- 刚体的矢量—矩阵描述
简介
我本意是为了学习理论力学,但是我对方向余弦矩阵的理解不够,所以不得不补习一下基础知识。这个过程里,我发现网上其他的文章当中,没有从方向余弦矩阵讲到理论力学的(但是有DCM&无人机的文章)。为了方便自己以后复习,我就把两个部分合并在一起写下来。第一次写文,若有不足望海涵
方向余弦矩阵
- 简介
百度百科的解释
方向余弦是指在解析几何里,一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。方向余弦是指在解析几何里,一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。
“方向余弦矩阵”是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系,也可以用来表达一个向量对于另一组标准正交基的方向余弦。
我的通俗理解
线性空间中的一个矢量,是不依赖坐标系的。但是在理论力学中,我们往往需要一个坐标系去描述该矢量。
涉及到多个坐标轴系时,就需要寻找同一矢量的不同坐标表示之间的关系。而这个关系就是方向余弦矩阵。
符号说明
| 符号 | 说明 |
|---|---|
| I , J \bm{I},\bm{J} I,J | O X Y OXY OXY坐标轴系的基向量 |
| i , j \bm{i},\bm{j} i,j | O x y Oxy Oxy坐标轴系的基向量 |
| r \bm{r} r | 目标矢量 |
| I i , I j , J i , J j I_i,I_j,J_i,J_j Ii,Ij,Ji,Jj… | I i I_i Ii为 I \bm{I} I在 i \bm{i} i上的投影的长度,其他类同 |
| ( r I , r J ) (r_I,r_J) (rI,rJ) | r \bm{r} r在 O X Y OXY OXY坐标轴系下的表示 |
| ( r i , r j ) (r_i,r_j) (ri,rj) | r \bm{r} r在 O x y Oxy Oxy坐标轴系下的表示 |
例子
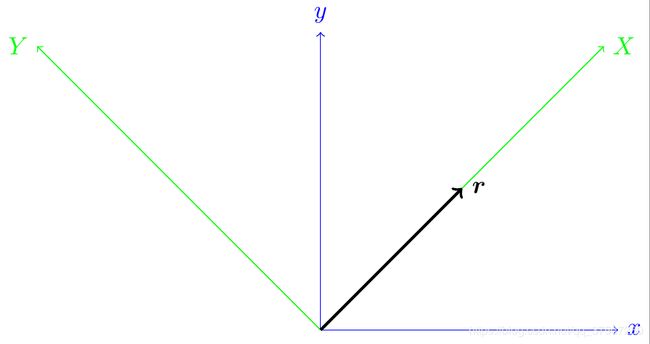
图中的矢量 r \bm{r} r(注意:矢量 r \bm{r} r与上面三个坐标系都没有关系)
请问:如何根据 ( r I , r J ) ({r_I},{r_J}) (rI,rJ),求出矢量 r \bm{r} r在 O x y Oxy Oxy坐标轴系下的坐标 ( r i , r j ) ({r_i},{r_j}) (ri,rj)?
反之,如果知道矢量 r \bm{r} r在 O x y Oxy Oxy坐标轴系下的坐标 ( r i , r j ) ({r_i},{r_j}) (ri,rj),如何求出 ( r I , r J ) ({r_I},{r_J}) (rI,rJ)?
这两个就需要方向余弦矩阵解答了。
2. 正题
Q1:根据 ( r i , r j ) ({r_i},{r_j}) (ri,rj),求出矢量 r \bm{r} r在 O X Y OXY OXY坐标轴系下的坐标 ( r I , r J ) ({r_I},{r_J}) (rI,rJ)
矢量 r \bm{r} r在 O X Y OXY OXY坐标轴系下的坐标为 ( r I , r J ) ({r_I},{r_J}) (rI,rJ),即:
r = r I I + r J J \bm{r} = r_I \bm{I}+r_J \bm{J} r=rII+rJJ
I , J \bm{I},\bm{J} I,J本身作为矢量,也是可以被 O x y Oxy Oxy表示的:
{ I = I i i + I j j J = J i i + J j j \begin{cases} \bm{I} = I_i \bm{i} + I_j \bm{j}\\ \bm{J} = J_i \bm{i} + J_j \bm{j} \end{cases} {I=Iii+IjjJ=Jii+Jjj
(注意:粗体 I I I和细体 I i , I j I_i,I_j Ii,Ij的差别)
带回后
r = r I I + r J J = r I ( I i i + I j j ) + r J ( J i i + J j j ) = ( r I I i + r J J i ) i + ( r I I j + r J J j ) j \begin {aligned} \bm{r}&=r_I \bm{I}+r_J \bm{J} \\ &= r_I ( I_i \bm{i} + I_j \bm{j})+r_J (J_i \bm{i} + J_j \bm{j}) \\ &=(r_I I_i + r_J J_i)\bm{i}+(r_I I_j + r_J J_j) \bm{j} \end {aligned} r=rII+rJJ=rI(Iii+Ijj)+rJ(Jii+Jjj)=(rIIi+rJJi)i+(rIIj+rJJj)j
( r i r j ) = ( r I I i + r J J i r I I j + r J J j ) = [ I i J i I j J j ] ( r I r J ) \left( \begin{matrix} r_i\\ r_j \end{matrix} \right)= \left( \begin{matrix} r_I I_i + r_J J_i\\ r_I I_j + r_J J_j \end{matrix} \right)= \left[ \begin{matrix} I_i & J_i \\ I_j & J_j \end{matrix} \right] \left( \begin{matrix} r_I \\ r_J \end{matrix} \right) (rirj)=(rIIi+rJJirIIj+rJJj)=[IiIjJiJj](rIrJ)
[ I i J i I j J j ] \left[ \begin{matrix} I_i & J_i \\ I_j & J_j \end{matrix} \right] [IiIjJiJj]就是方向余弦矩阵,按列展开,第一列表示 I \bm{I} I在 O x y Oxy Oxy坐标轴系下的坐标 I O x y \bm{I}^{Oxy} IOxy,第二列表示 J \bm{J} J在 O x y Oxy Oxy坐标轴系下的坐标 J O x y \bm{J}^{Oxy} JOxy,记作 [ I J ] O x y \left[ \begin{matrix}\bm{I} & \bm{J}\end{matrix}\right]^{Oxy} [IJ]Oxy。
具体矩阵的每一个元素的值是多少呢?
[ I J ] O x y = [ I ⋅ i ∥ i ∥ J ⋅ i ∥ i ∥ I ⋅ j ∥ j ∥ J ⋅ j ∥ j ∥ ] = [ ∥ I ∥ c o s ( I , i ) ∥ J ∥ c o s ( J , i ) ∥ I ∥ c o s ( I , j ) ∥ J ∥ c o s ( J , j ) ] \left[ \begin{matrix}\bm{I} & \bm{J}\end{matrix}\right]^{Oxy}= \left[ \begin{matrix} \frac{\bm{I \cdot i}}{\|{\bm{i}}\|} & \frac{\bm{J \cdot i}}{\|{\bm{i}}\|} \\ \frac{\bm{I \cdot j}}{\|{\bm{j}}\|} & \frac{\bm{J \cdot j}}{\|{\bm{j}}\|} \end{matrix} \right]= \left[ \begin{matrix} {\|\bm{I}\|}cos(\bm{I},\bm{i}) & {\|\bm{J}\|}cos(\bm{J},\bm{i}) \\ {\|\bm{I}\|}cos(\bm{I},\bm{j}) & {\|\bm{J}\|}cos(\bm{J},\bm{j}) \end{matrix} \right] [IJ]Oxy=[∥i∥I⋅i∥j∥I⋅j∥i∥J⋅i∥j∥J⋅j]=[∥I∥cos(I,i)∥I∥cos(I,j)∥J∥cos(J,i)∥J∥cos(J,j)]
当 ∥ I ∥ , ∥ J ∥ \|\bm{I}\|,\|\bm{J}\| ∥I∥,∥J∥均为 1 1 1时
[ I J ] O x y = [ I ⋅ i J ⋅ i I ⋅ j J ⋅ j ] = [ c o s ( I , i ) c o s ( J , i ) c o s ( I , j ) c o s ( J , j ) ] \left[ \begin{matrix}\bm{I}&\bm{J}\end{matrix}\right]^{Oxy}= \left[ \begin{matrix} {\bm{I \cdot i}} & {\bm{J \cdot i}} \\ {\bm{I \cdot j}} & {\bm{J \cdot j}} \end{matrix} \right]= \left[ \begin{matrix} cos(\bm{I},\bm{i}) & cos(\bm{J},\bm{i}) \\ cos(\bm{I},\bm{j}) & cos(\bm{J},\bm{j}) \end{matrix} \right] [IJ]Oxy=[I⋅iI⋅jJ⋅iJ⋅j]=[cos(I,i)cos(I,j)cos(J,i)cos(J,j)]
类似地:
[ i j ] O X Y = [ i ⋅ I j ⋅ I i ⋅ J j ⋅ J ] = [ c o s ( i , I ) c o s ( j , I ) c o s ( i , J ) c o s ( j , J ) ] \left[ \begin{matrix}\bm{i}&\bm{j}\end{matrix}\right]^{OXY}= \left[ \begin{matrix} {\bm{i \cdot I}} & {\bm{j \cdot I}} \\ {\bm{i \cdot J}} & {\bm{j \cdot J}} \end{matrix} \right]= \left[ \begin{matrix} cos(\bm{i},\bm{I}) & cos(\bm{j},\bm{I}) \\ cos(\bm{i},\bm{J}) & cos(\bm{j},\bm{J}) \end{matrix} \right] [ij]OXY=[i⋅Ii⋅Jj⋅Ij⋅J]=[cos(i,I)cos(i,J)cos(j,I)cos(j,J)]
根据方向余弦矩阵,就能变换矢量 r \bm{r} r的坐标表示。
3. 性质
- [ I J ] O x y \left[ \begin{matrix}\bm{I}&\bm{J}\end{matrix}\right]^{Oxy} [IJ]Oxy的转置等于 [ i j ] O X Y \left[ \begin{matrix}\bm{i}&\bm{j}\end{matrix}\right]^{OXY} [ij]OXY
- 方向余弦矩阵为正交矩阵
(证明:因为 I ⋅ J = 0 I \cdot J = 0 I⋅J=0所以 I O x y ⋅ J O x y = 0 I^{Oxy}\cdot J^{Oxy} = 0 IOxy⋅JOxy=0) - n阶方向余弦矩阵只有n个自由量
以三维坐标轴系为例,做一个不严谨但直观的解释:确定一个坐标轴系A只需要知道任意两个坐标轴,就可以确定第三条轴,从而确定整个坐标轴系;坐标轴A旋转至坐标轴B的夹角也是一个三维向量,从而就能确定坐标轴B。综上,3阶方向余弦矩阵需要3个自由量。
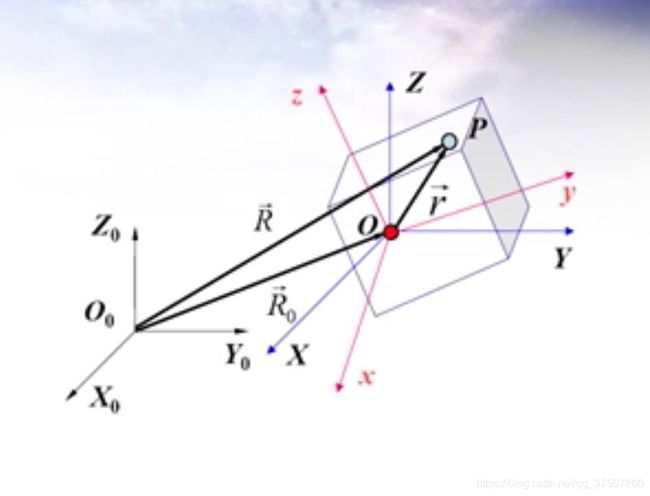
刚体的矢量—矩阵描述
| 符号 | 说明 |
|---|---|
| O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0 | 固定坐标系 |
| O X Y Z OXYZ OXYZ | 平动坐标系,由 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0 平移得到 |
| O x y z Oxyz Oxyz | 固连坐标系,由 O X Y Z OXYZ OXYZ旋转得到 |
| ρ ‾ \underline{\rho} ρ | r \bm{r} r在 O x y z Oxyz Oxyz下的坐标,为常数 |
| r ‾ \underline{r} r | r \bm{r} r在 O X Y Z OXYZ OXYZ下的坐标,随着刚体旋转而发生变化 |
| A A A | 从 O x y z Oxyz Oxyz到 O X Y Z OXYZ OXYZ的方向余弦矩阵,随着刚体旋转而发生变化( r ‾ = A ρ ‾ \underline{r} = A\underline{\rho} r=Aρ, ρ ‾ = A − 1 r ‾ = A T r ‾ \underline{\rho} = A^{-1} \underline{r}=A^{T} \underline{r} ρ=A−1r=ATr) |
如何求得 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0坐标系下, 刚体上任意一点的轨迹方程?
不考虑任何坐标轴系
R = R 0 + r \bm{R} = \bm{R_0}+\bm{r} R=R0+r
在 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0下
R ‾ = R 0 ‾ + r ‾ = R 0 ‾ + A ρ ‾ \underline{R} = \underline{R_0}+\underline{r} = \underline{R_0}+{ A\underline{\rho}} R=R0+r=R0+Aρ
刚体上任意一点的运动可以由一个向量 R 0 R_0 R0和一个矩阵 A A A描述
{ R 0 = R 0 ( t ) — — 描 述 平 动 A = A ( t ) — — 描 述 刚 体 相 对 于 基 点 的 转 动 ( 定 点 运 动 ) \begin{cases} \bm{R_0} = \bm{R_0(t)}——描述平动\\ \bm{A} = \bm{A(t)}——描述刚体相对于基点的转动(定点运动) \end{cases} {R0=R0(t)——描述平动A=A(t)——描述刚体相对于基点的转动(定点运动)
因此,一般刚体的运动可以分解为基点的平动和相对于基点的转动(定点运动)。
由于 R 0 \bm{R_0} R0有三个自由量,正交矩阵 A \bm{A} A有三个自由量,因此描述刚体运动需要六个独立参数。
如何求得 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0坐标系下, 刚体上任意一点的速度方程?
在 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0下对 R ‾ = R 0 ‾ + A ρ ‾ \underline{R} = \underline{R_0}+{ A\underline{\rho}} R=R0+Aρ求导:
R ‾ ˙ = R 0 ‾ ˙ + A ρ ‾ ˙ + A ρ ‾ ˙ = R 0 ‾ ˙ + A A T r ‾ ˙ + A ρ ‾ ˙ \dot{\underline{R}} = \dot{\underline{R_0}}+\dot{{ A}\underline{\rho}}+A\dot{\underline{\rho}}=\dot{\underline{R_0}}+\dot{{ A}A^T\underline{r}}+A\dot{\underline{\rho}} R˙=R0˙+Aρ˙+Aρ˙=R0˙+AATr˙+Aρ˙
由于 ρ ‾ \underline{\rho} ρ是常数,所以 A ρ ‾ ˙ = 0 A\dot{\underline{\rho}}=0 Aρ˙=0,因此
R ‾ ˙ = R 0 ‾ ˙ + A A T r ‾ ˙ \dot{\underline{R}} =\dot{\underline{R_0}}+\dot{{ A}A^T\underline{r}} R˙=R0˙+AATr˙

因此
v ‾ = R ‾ ˙ = R 0 ‾ ˙ + ω ~ r ‾ = R 0 ‾ ˙ + ω × r ‾ \underline{{v}} =\dot{\underline{R}} =\dot{\underline{R_0}}+\tilde{\omega}\underline{r}=\dot{\underline{R_0}}+\omega\times \underline{r} v=R˙=R0˙+ω~r=R0˙+ω×r
其中 R 0 ‾ ˙ \dot{\underline{R_0}} R0˙代表基点的平动速度, r ‾ ˙ = ω × r ‾ \dot{\underline{r}}=\omega\times \underline{r} r˙=ω×r代表相对于基点的转动速度。
如何求得 O 0 X 0 Y 0 Z 0 O_0X_0Y_0Z_0 O0X0Y0Z0坐标系下, 刚体上任意一点的加速度方程?
a ‾ = v ‾ ˙ = R 0 ‾ ¨ + ω ˙ × r ‾ + ω × r ‾ ˙ = R 0 ‾ ¨ + ω ˙ × r ‾ + ω × ( ω × r ‾ ) \underline{{a}} = \dot{\underline{v}} =\ddot{\underline{R_0}}+\dot{\omega}\times \underline{r}+\omega\times \dot{\underline{r}}=\ddot{\underline{R_0}}+\dot{\omega}\times \underline{r}+\omega\times (\omega\times \underline{r}) a=v˙=R0¨+ω˙×r+ω×r˙=R0¨+ω˙×r+ω×(ω×r)
a ‾ = a 0 ‾ + ε × r ‾ + ω × ( ω × r ‾ ) \underline{{a}} = \underline{a_0}+{\varepsilon}\times \underline{r}+\omega\times (\omega\times \underline{r}) a=a0+ε×r+ω×(ω×r)
其中
{ a 0 ‾ = R 0 ‾ ¨ 基 点 的 加 速 度 ε × r ‾ 转 动 加 速 度 ( 其 中 ε = ω ˙ ) ω × ( ω × r ‾ ) 向 ( 轴 ) 心 加 速 度 \begin{cases} \underline{a_0}=\ddot{\underline{R_0}} & 基点的加速度\\ {\varepsilon}\times \underline{r} & 转动加速度(其中\varepsilon = \dot{\omega})\\ \omega\times (\omega\times \underline{r}) &向(轴)心加速度 \end{cases} ⎩⎪⎨⎪⎧a0=R0¨ε×rω×(ω×r)基点的加速度转动加速度(其中ε=ω˙)向(轴)心加速度
参考:
理论力学-刚体运动的矩阵与向量描述
https://wenku.baidu.com/view/7e699e4e8e9951e79b892757.html