Redis详解：Redis底层数据结构（下）

Redis底层数据结构（上）：https://blog.csdn.net/qq_40378034/article/details/89295462

四、跳跃表

跳跃表是一种有序数据结构，它通过在每个节点中维持多个指向其他节点的指针，从而达到快速访问节点的目的

跳跃表支持平均$O(logN)$、最坏O(N)复杂度的节点查找，还可以通过顺序性操作来批量处理节点

Redis使用跳跃表作为有序集合键的底层实现之一，如果一个有序集合包含的元素数量比较多，又或者有序集合中元素的成员是比较长的字符串时，Redis就会使用跳跃表来作为有序集合键的底层实现

Redis只在两个地方用到了跳跃表，一个是实现有序集合键，另一个是在集群节点中用作内部数据结构

1、跳跃表的实现

Redis的跳跃表由redis.h/zskiplistNode和redis.h/zskiplist两个结构定义，其中zskiplistNode结构用于表示跳跃表节点，而zskiplist结构则用于保存跳跃表节点的相关信息，比如节点的数量，以及指向表头节点和表尾节点的指针等等

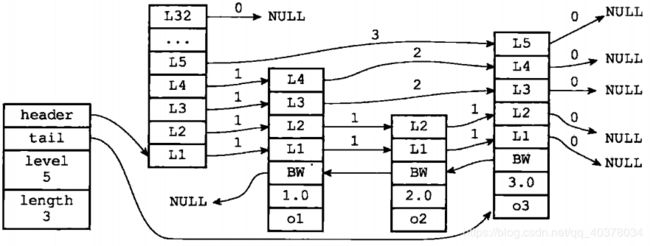
上图中一个跳跃表示例，位于图片最左边的是zskiplist结构，该结构包含以下属性：

• header：指向跳跃表的表头节点
• tail：指向跳跃表的表尾节点
• level：记录目前跳跃表内，层数最大的那个节点的层数
• length：记录跳跃表的长度，也即是，跳跃表目前包含节点的数量

位于zskiplist结构右方的是四个zskiplistNode结构，该结构包含以下属性：

• 层：节点中用L1、L2、L3等标记节点的各个层，L1代表第一层、L2代表第二层，每个层都带有两个属性：前进指针和跨度。前进指针用于访问表尾方向的其他节点，而跨度则记录了前进指针所指向节点和当前节点的距离
• 后退指针：节点中用BW字样标记节点的后退指针，它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用
• 分值：各个节点中的1.0、2.0和3.0是节点所保存的分值。在跳跃表中，节点按各自所保存的分值从小到大排列
• 成员对象：各个节点的o1、o2、o3是节点所保存的成员对象

1）、跳跃表节点

typedef struct zskiplistNode{
	// 后退指针
	struct zskiplistNode *backward;
    
	// 分值
	double score;
    
	// 成员对象
	robj *obj;
    
	// 层
	struct zskiplistLevel{
		// 前进指针
        struct zskiplistNode *forward;
        
		// 跨度
		unsigned int span;
    }level[];
    
}zskiplistNode;

1）层

跳跃表节点的level数组可以包含多个元素，每个元素都包含一个指向其他节点的指针，程序可以通过这些层来加快访问其他节点的速度，一般来说，层的数量越多，访问其他节点的速度就越快

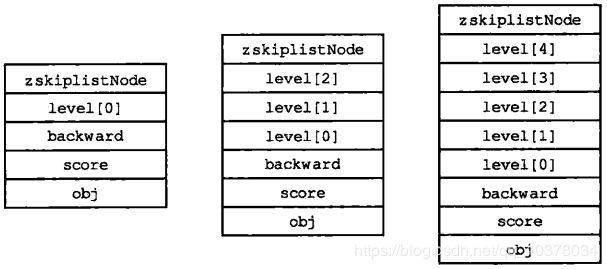
每次创建一个新跳跃表节点的时候，程序都根据幂次定律（越大的数出现的概率越小）随机生成一个介于1和32之间的值作为level数组的大小，这个大小就是层的高度

下图中分别展示了三个高度为1层、3层和5层的节点

2）前进指针

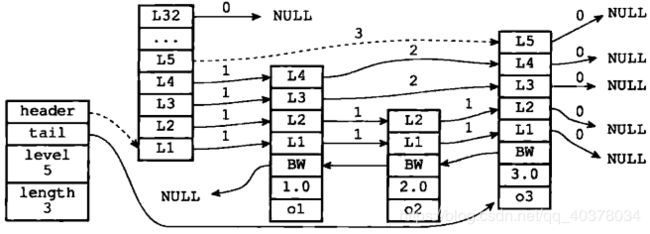
每个层都有一个指向表尾方向的前进指针，用于从表头向表尾方向访问节点

下图中用虚线表示出了程序从表头向表尾方向，遍历跳跃表中所有节点的路径

3）跨度

层的跨度用于记录两个节点之间的距离

• 两个节点之间的跨度越大，它们相距得就越远
• 指向NULL的所有前进指针的跨度都为0，因为它们没有连向任何节点

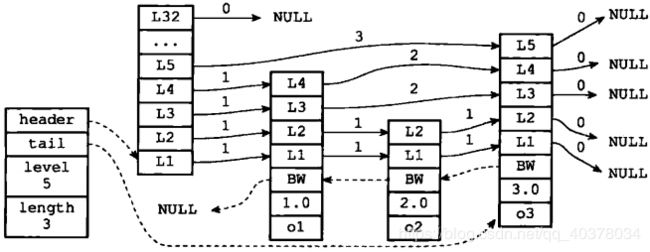
跨度实际上是用来计算排位的：在查找某个节点的过程中，将沿途访问过的所有层的跨度累计起来，得到的结果就是目标节点在跳跃表中的排位

上图中用虚线标记了在跳跃表中查找分值为3.0、成员对象为o3的节点时，沿途经历的层：查找的过程中只经过了一个层，并且层的跨度为3，所有目标节点在跳跃表中的排位为3

4）后退指针

节点的后退指针用于从表尾向表头方向访问节点：跟可以一次跳过多个节点的前进指针不同，因为每个节点只有一个后退指针，所以每次只能后退至前一个节点

5）分值和成员

节点的分值是一个double类型的浮点数，跳跃表中的所有节点都按分值从小到大来排序

节点的成员对象是一个指针，它指向一个字符串对象，而字符串对象则保存着一个SDS值

在同一个跳跃表中，各个节点保存的成员对象必须是唯一的，但是多个节点保存的分值却可以是相同的：分值相同的节点将按照成员对象在字典序中的大小来进行排序，成员对象较小的节点会排在前面（靠近表头的方向），而成员对象较大的节点则会排在后面（靠近表尾的方向）

2）、跳跃表

typedef struct zskiplist {
	//表头节点和表尾节点
	structz skiplistNode *header,*tail;
    
	//表中节点数量
	unsigned long length;
    
	//表中层数最大的节点的层数
	int level;
}zskiplist;

header和tail指针分别指向跳跃表的表头和表尾节点，通过这两个指针，程序定位表头节点和表尾节点的复杂度为O(1)

通过使用length属性来记录节点的数量，程序可以在O(1)复杂度内返回跳跃表的长度

level属性则用于在O(1)复杂度内获取跳跃表中层高最大的那个节点的层数量，表头节点的层高不计算在内

五、整数集合

整数集合是集合键的底层实现之一，当一个集合只包含整数值元素，并且这个集合的元素数量不多时，Redis就会使用整数集合作为集合键的底层实现

127.0.0.1:6379> SADD numbers 1 3 5 7 9
(integer) 5
127.0.0.1:6379> OBJECT ENCODING numbers
"intset"

1、整数集合的实现

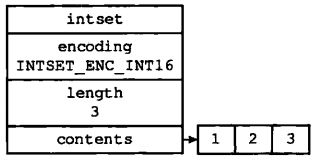
整数集合是Redis用于保存整数值的集合抽象数据结构，它可以保证类型为int16_t、int32_t、int64_t的整数值，并且保证集合中不会出现重复元素

typedef struct intset{
	// 编码方式
    uint32_t enconding;
    
	// 集合包含的元素数量
	uint32_t length;
    
	// 保存元素的数组    
	int8_t contents[];
}intset;

contents数组是整数集合的底层实现：整数集合的每个元素都是contents数组的一个数组项，各个项在数组中按值的大小从小到大有序地排列，并且数组中不包含任何重复项

length属性记录了整数集合包含的元素数量，也即是contents数组的长度

contents数组的真正类型取决于enconding属性的值

2、升级

每当我们要将一个新元素添加到整数集合里面，并且新元素的类型比整数集合现有所有元素的类型都要长时，整数集合需要先进行升级，然后才能将新元素添加到整数集合里面

升级整数集合并添加新元素共分为三步进行：

1）、根据新元素的类型，扩展整数集合底层数组的空间大小，并为新元素分配空间

2）、将底层数组现有的所有元素都转换成与新元素相同的类型，并将类型转换后的元素放置到正确的位上，而且在放置元素的过程中，需要继续维持底层数组的有序性质不变

3）、将新元素添加到底层数组里面

一个包含三个int16_t类型的元素的整数集合：

contents数组的各个元素，以及它们所在的位：

进行空间重分配之后的数组：

从int16_t类型转换为int32_t类型：

添加新元素到数组中：

3、升级的好处

整数集合的升级策略有两个好处，一个是提升整数集合的灵活性，另一个是尽可能地节约内存

4、降级

整数集合不支持降级操作，一旦对数组进行了升级，编码就会一直保持升级后的状态

六、压缩列表

压缩列表是列表建和哈希键的底层实现之一。当一个列表键只包含少量列表项，并且每个列表项要么就是小整数值，要么就是长度比较短的字符串，那么Redis就会使用压缩列表来做列表键的底层实现。当一个哈希键只包含少量键值对，而且每个键值对的键和值要么就是小整数值，要么就是长度比较短的字符串，那么Redis就会使用压缩列表来做哈希键的底层实现

1、压缩列表的构成

压缩列表是Redis为了节约内存而开发的，是由一系列特殊编码的连续内存块组成的顺序型数据结构。一个压缩列表可以包含任意多个节点，每个节点可以保存一个字节数组或者一个整数值

压缩列表各个组成部分的详细说明：

2、压缩列表节点的构成

压缩列表节点的各个组成部分：

1）、previous_entry_length

节点的previous_entry_length属性以字节为单位，记录了压缩列表中前一个节点的长度。previous_entry_length属性的长度可以是1字节或者5字节：

• 如果前一节点的长度小于254字节，那么previous_entry_length属性的长度为1字节：前一节点的长度就保存在这一个字节里面
• 如果前一个节点的长度大于254字节，那么previous_entry_length属性的长度为5字节：其中属性的第一字节会被设置为0xFE（十进制254），而之后的四个字节则用于保存前一节点的长度

因为节点的previous_entry_length属性记录了前一个节点的长度，所以程序可以通过指针运算，根据当前节点的起始位置来计算出前一个节点的起始位置

2）、encoding

节点的encoding属性记录了节点的content属性所保存数据的类型以及长度

3）、content

节点的content属性负责保存节点的值，节点值可以是一个字节数组或者整数，值的类型和长度由节点的encoding属性决定

3、连锁更新

如果在一个压缩列表中，有多个连续的、长度介于250字节到253字节之间的节点e1至eN

因为e1至eN的所有节点的长度都小于254字节，所以记录这些节点的长度只需要1字节长的previous_entry_length属性，e1至eN的所有节点的previous_entry_length属性都是1字节长的

如果我们将一个长度大于等于254字节的新节点new设置为压缩列表的表头节点，那么new将成为e1的前置节点

因为e1的previous_entry_length属性仅长1字节，它没办法保存新节点new的长度，所以程序将对压缩列表执行空间重分配操作，并将e1节点previous_entry_length属性从原来的1字节长扩展5字节长

e1原来的长度介于250字节至253字节之间，在为previous_entry_length属性新增四个字节的空间之后，e1的长度就变成了介于254字节至257字节之间，而这种长度使用1字节长的previous_entry_length属性是没办法保存的

因此，为了让e2的previous_entry_length属性可以记录下e1的长度，程序需要再次对压缩列表执行空间重分配操作，并将e2节点的previous_entry_length属性从原来的1字节长扩展为5字节长

正如扩展e1引发了对e2的扩展一样，扩展e2也会引发对e3的扩展，而扩展e3又会引发对e4的扩展……为了让每个节点的previous_entry_length属性都符合压缩列表对节点的要求，程序需要不断地对压缩列表执行空间重分配操作，直到eN为止

Redis将这种在特殊情况下产生的连续多次空间扩展操作称之为连锁更新

删除节点也可坑引发连锁更新，如果e1至eN都是大小介于250字节至253字节的节点，big节点的长度大于等于254字节，而small节点的长度小于254字节，那么我们将small节点从压缩列表中删除之后，为了让e1的previous_entry_length属性可以记录big节点的长度，程序将扩展e1的空间，并由此引发之后的连锁更新

因为连锁更新在最坏情况下需要对压缩列表执行N次空间重分配操作，而每次空间重分配的最坏复杂度为O(N)，所以连锁更新的最坏复杂度为$O(N^2)$

尽管连锁更新的复杂度较高，但它真正造成性能问题的几率是很低的

• 首先，压缩列表要恰好有多个连续的、长度介于250字节至253字节之间的节点，连锁更新才有可能被引发
• 其次，即使出现连锁更新，但只要被更新的节点数量不多，就不会对性能造成任何影响

ziplistPush等命令的平均复杂度仅为O(N)