强化学习(四) - 无模型学习(MC、TDL)
上一节讲的是在已知模型的情况下,通过动态规划来解决马尔科夫决策过程(MDP)问题。具体的做法有两个:一个是策略迭代,一个是值迭代。
从这一节开始,我们将要进入模型未知的情况下,如何去解决MDP问题。
模型未知,即状态转移概率 P s s ′ a P^a_{ss′} Pss′a 这些我们是不知道的。所以我们无法直接利用如下Bellman方程来求解V和Q值得到最优策略。
![]()
所以,为了能够从环境中学习,我们需要让agent与environment交互,得到一些经历(样本)。然后通过这些经历来进行策略评估与策略迭代,从而最终得到最优策略。
这种做法的理论是从蒙特卡罗方法中来的。所以我们先讲蒙特卡罗学习。接着从蒙特卡罗的缺点出发,进一步讲解了时序差分学习以及λ时序差分强化学习。
Monte-Carlo Learning(蒙特卡罗学习)
蒙特卡罗方法又叫做统计模拟方法,它使用随机数(或伪随机数)来解决计算问题。
比如下图,矩形的面积我们可以轻松得到,但是对于阴影部分的面积计算困难。所以为了计算阴影部分的面积,我们可以在矩形上均匀地撒豆子,然后统计在阴影部分的豆子数占总的豆子数的比例,就可以估算出阴影部分的面积。
对于无模型强化学习,虽然我们不知道状态转移概率P,但是这个概率是真实存在的。我们可以直接去尝试、不断采样,然后会得到奖赏,通过奖赏来评估值函数。这个想法与蒙特卡罗方法的思想是一致的,我们可以尝试很多次,最后估计的V值就会很接近真实的V值了。
episode
episode就是经历,每条episode就是一条从起始状态到结束状态的经历(路径)。

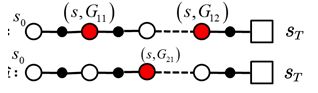
首先我们要得到的是某一个状态s的平均收获。所以我们说的episode要经过状态s。所以上图中第二条路径没有经过状态s,对于s来说就不能使用它了。而且最后我们episode都是要求达到终点的,才能算是一个episode。
蒙特卡罗学习是指在不清楚MDP状态转移概率及即时奖励的情况下,直接从经历完整的Episode来学习状态价值,通常情况下某状态的价值等于在多个Episode中以该状态算得的所有收获的平均。
在蒙特卡罗方法中,计算状态s在每一个样本中的回报的均值分为first visit 和every visit两种方法。
first visit: 在计算状态s处的值函数时,只利用每次实验(episode)中第一次访问到状态s时返回的值。如上图所示,计算s出的均值只利用了G11( G表示从s开始一直到终点的所有R之和 ),因此计算公式如下:

every visit : 在计算状态s处的值函数时,利用所有访问到状态s时的回报返回值。即:

所以,蒙特卡罗学习就是指不基于模型本身,而是直接从经历过的episode中进行学习,通过不同episode的平均收获值替代价值函数。
Monte-Carlo Policy Evaluation(蒙特卡罗策略评估)
蒙特卡罗策略评估使用多个episodes的平均获得值来代替这个状态价值函数。

N(s)表示状态s出现的次数。每次状态s出现,N(s)加1。
上面的做法需要等到所有的episodes都经历完了,再去计算V(s)。
其实可以使用Incremental mean(累进更新平均值)。具体的做法就是:
对于每来一个episode: S 1 , A 1 , R 2 , S 2 , A 2 , . . . , S t , A t , R t + 1 , . . . , S k S_1,A_1,R_2,S_2,A_2,...,S_t,A_t,R_{t+1},...,S_k S1,A1,R2,S2,A2,...,St,At,Rt+1,...,Sk
对于episode里的每一个状态 S t S_t St,有一个收获 G t G_t Gt。每碰到一次 S t S_t St,使用下面的式子计算状态的平均价值V(s):


Temporal-Difference Learning(时序差分学习)
TD Learning中会把 G t G_t Gt写成递归的形式。这样,每走一步都可以更新一次V。
而蒙特卡罗中,却需要走完整个episode,才能得到 G t G_t Gt,从而更新一次V。 蒙特卡罗学习方法的更新是这样的:
![]()
在TD learning中,算法在估计 G t G_t Gt时,用的是离开该状态时的即时奖励 R t + 1 R_{t+1} Rt+1与下一个状态 S t + 1 S_{t+1} St+1的预估状态价值乘以折扣因子γ组成:(用目标值 R t + 1 + γ V ( S t + 1 ) R_{t+1}+γV(S_{t+1}) Rt+1+γV(St+1)代替 G t G_t Gt)

区别:
蒙特卡罗每次更新都需要等到agent到达终点之后再更新;
而对于TD learning来说,agent每走一步它都可以更新一次,不需要等到到达终点之后才进行更新
MC、TDL、DP 总结
Monte-Carlo, Temporal-Difference 和Dynamic Programming这三种学习方法都是用来计算状态价值的。
它们的区别在于:
前两种是在无模型下常用的方法,而MC方法又需要一个完整的episode来更新状态价值,TD则不需要完整的episode(单步更新)。
DP方法则是基于模型的计算状态价值的方法。它通过计算一个状态S所有可能的转移状态S’及其转移概率以及对应的即时奖励来计算这个状态S的价值。也正是因为它知道整个模型的情况(知道状态转移概率与即时奖励),所以它才能够这样子计算全面的情况。
下图中的这颗树,代表了整个状态与动作空间。对于蒙特卡罗方法来说,要更新一次V值,需要有一个完整的样本(即图中红色部分就是一个样本)。这条路径经过了三个状态,所以可以更新三个状态的V值。

下图的红色部分是TDL每次更新所需要的。对于MC和TDL来说,它们都是无模型的,所以它们只能通过尝试来近似真实值。
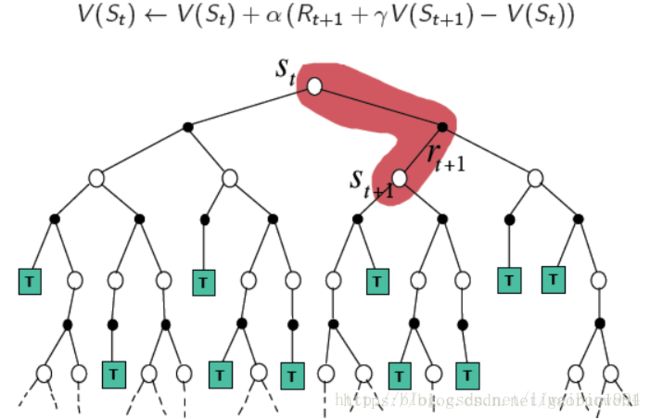
这是动态规划的V值计算,由于知道了模型,所以可以直接计算期望V值。

参考:
强化学习(四):蒙特卡罗学习(MonteCarlo)与时序差分学习(TD learning)