图形学中的光和辐射学（Radiometry）

最近重读Realtime Rendering 一书，对书中光照模型等内容有些感受；准备写些笔记记录一下自己的认识。本篇先主要讲讲辐射学（Radiometry）和简单光照模型；后面会讲讲BRDF及其实现吧。

光

光的本质其实很复杂，物理学至今仍没完全搞清楚；它是一种电磁辐射但却有波粒二相性。幸好我们研究的是图形学不是量子物理。图形学的光只是个近似；我们只要想象它会向空间发射带有能量的光子（particles），然后这些光子会和物体表面发生作用（反射，折射和吸收）。最后的结果是我们看到了物体的颜色和各种纹理。

然后因为能量守恒，所以入射光等于被反射的光加吸收的光再加折射的光。

light incident at surface = light reflected + light absorbed + light transmitted

辐射学（Radiometry）

为了计算物体表面的颜色值（Shading），我们首先必须考虑光在空间中的分布以及能量是如何从光源传播到物体表面的。这是辐射学的范畴。考虑如下图所示的空间中的点光源：

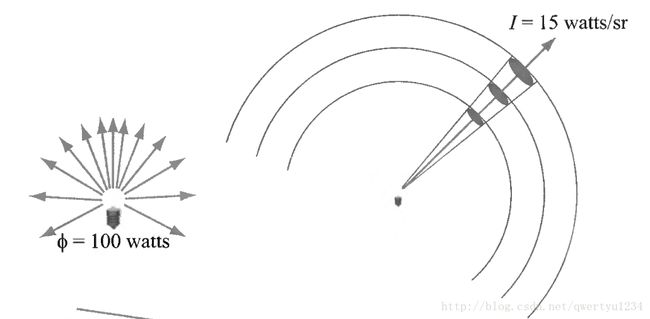
在同一方向上，近处的较小的表面和远处较大的接收到的光子能量应该相同。这说明方向角很重要；以该点为顶点的圆锥内，所有表面接收到的光子能量是一样的。
所以这里要引出固体角的概念。

固体角（Solid Angle)

先看平面上角度的定义，然后再引申到空间。

如上图所示：平面上角度是所围成的扇形的弧长除以半径；

dφ = （dl*cosθ） / r

单位是弧度，整个圆周就是2π。
而引申到空间，就是围成的圆锥在球体表面的投影除以半径的平方。

dω = （dA*cosθ） / （r*r）

由半球面面积公式容易知道这个比值是常量，与球的半径无关的。这就是我们要的方向角，整个球面就是4π。

从上面的图可以计算出相对与球体坐标：

dω = sinθdθdφ

这是后面要用到的结果。

Radiance & Luminance

光源首先是个辐射源，它会向周围辐射能量Q；也就是其的基本物理量是功率W。然而，光源消耗的能量不可能全部转换为光能。光通量就是衡量光源中光能的那部分功率。
这里还要插一部分关于可见光测量的概念。上面提到的都是辐射学，适用于所有电磁辐射。而具体到可见光，它的所有概念（如光通量，光照强度）都跟视觉函数有关。
如下图：

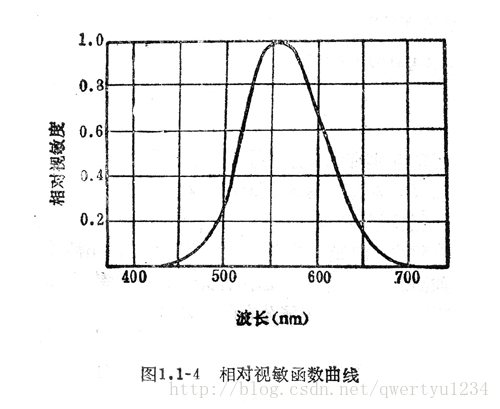
这就是为什么人眼感觉绿光会比红光或者蓝光亮。明视觉下，同功率的光源，555纳米的绿光看起来是最亮的。

辐射学（Radiometry）	色度学（Photometry）
辐射通量（radiant flux） Watt	光通量（luminous flux） lm
辐射照度（irradiance）	光照度（illuminance） lux
辐射强度（radiant intensity）	光照强度（luminance intensity）
辐射亮度（radiance）	光亮度（luminance） nit

这两组概念在数量上的差别只是CIE的标准视觉函数；其物理意义差别在于色度学的概念引入了人的主观感受，也就是同样的能量，不同颜色的光人感受到的亮度不一样。除了这个主观因素，它们背后的物理意义是一样的。所以下面的讨论中有时并没有区分这两组概念；而实际图形学用的都是RGB三分量。

光通量（Φ）
光源在单位时间内，向周围空间辐射出使人眼产生感觉的能量，称为光通量。用符号Φ表示，实用单位为流明（lm），简称流。单位电功率所发出的流明数（lm/w），称为发光效率。1流明相当于1/680W的单色光源辐射的能量。

Φ = dQ / dt

光源是向周围辐射能量的，所以在每个方向上其光通量并不一定相同。比如手电筒，聚光前灯泡可能是均匀向四周发光，但聚光后它的光束全部向一特定范围内发射，这样该方向就会比较明亮。所以光源的明亮度是和方向有关，某一方向上辐射能量越多自然越亮。而与力学的单位比较，光通量相当于压力，而发光强度相当于压强。要想被照射点看起来更亮，不仅要提高光通量，而且要增大会聚的手段，实际上就是减少面积，这样才能得到更大的强度。

发光强度（I）
光源在某一特定方向上单位立体角（球面度sr）内辐射的光通量，称为光源在该方向上的发光强度，简称光强，用符号I表示，单位为坎德拉（cd），简称坎。 1（cd）=1（lm）/1（sr）。

实际经常要考虑的是光源照射某一表面的情况；也就是光相对于空间中某一表面A的分布情况。

E = dΦ / dA

照度（E）
衡量的是某一表面A上所有入射光的光通量。
还有个辐射出射照度（M，radiosity），是某一表面所有发出的光的光通量。
勒克司(lux，法定符号lx)是照度(Illuminance)的单位。等于1流明的光通量均匀照在1平方米表面上所产生的照度。

对于理想的单一方向光源（directional light），其照度在它的方向上是常数E。而实际的光源，其照度往往和物体与光源距离有关。可以考虑下图所示的点光源。

在某一方向角内，发光强度是I；该方向上所有面照射到的光通量是一样的。但是，很明显离光源越近光线越密集，单位面积上的光通量也越大。

E = I*ω / A
ω = A / （r*r）
E = I / （r*r）

对更一般的情况，有：

dΦ = I*dω = E*dA
L = I/dA = E/dω

而图形学中经常使用和关心的量是亮度（L）。这是因为人眼或是图像传感器感受到的光强是和这个亮度成正比的。

而图形学中最关键的计算是Shading；也就是计算物体表面任意点相对于Camera位置的亮度（L）。Camera相当于人的眼睛，它观察到的值直接正比与亮度。

而一般物体本身并不发光，人眼观测到某一点的亮度是直接正比于该点附近微小面dA所接收到的光强，也就是照度E，如下图所示：

光亮度(luminance)
是表示发光面明亮程度的，以L表示，指发光表面在指定方向的发光强度与垂直于指定方向的发光面的面积之比，单位是坎德拉/平方米。

空间中光的分布是和方向有关的；对于某一位置p上的微小表面dA，radiance是：

而其他物理量则可以表示为：

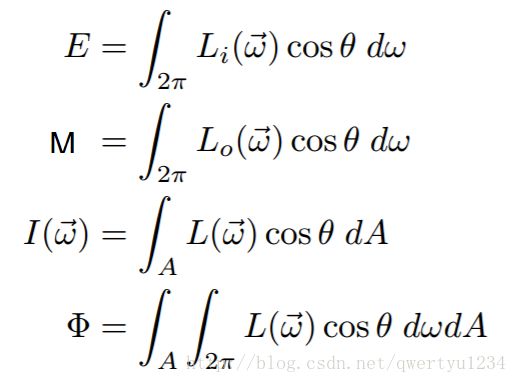
Radiance在空间中的分布实际取决于位置和方向；它是一个5个参数的函数：L(x1,y1,z1,θ,φ) 3个参数决定位置，另外两个决定方向（θ,φ是球面坐标）。
Radiance&Luminance有这么几个特性：

• 图像传感器、人眼或者照相机感受或测量的量直接正比于Radiance
• 图形学中主要就是计算这个量
• 在光线传播方向（Ray）上，Radiance是保持不变的
• Radiance是和距离无关的。
  首先看第3点，也就是光从一个微表面传播到另一个微表面，L值是一样的，如下图：
  
  这个可以由能量守恒得到证明，即出射光和入射光的能量L*dω*dA是一样的。
  
  然后看第1点，这也是为什么我们最关心也是最后的计算结果是亮度的原因。考虑下图所示的简单传感器模型：
  
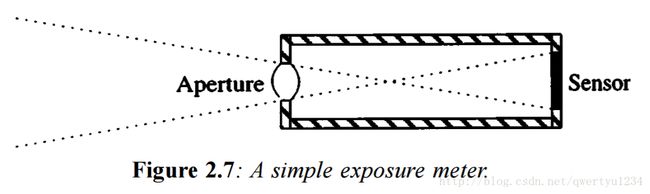
  盒子里后挡板黑色区域是图像传感器，它的感光面积是a；而整个装置的孔径是A。所以当该装置装好后，它的可感受光的区域就确定了，也就是相当于图形学里Camera的视锥体确定了。所以整个感光面接收到的光的能量是：
  
  如果空间中光亮度L是恒定的，则传感器接收到的光通量正比于亮度L。由以上推导可以看出图像传感器装置的输出受光亮度影响，它的输出信号应该取决于传感器装置自身几何参数（a，A)和空间光亮度。

光源模型

一般图形学主要光源模型是单一方向光和理想点光源。其中前者是Luminance在它的方向上常量；后者是整个空间发光强度I是常量。
下图是两者光源的物理量：

还有一种Spot light，其实是点光源的扩展；它是在某范围内发光强度是一个和方向有关的简单函数。具体参考Realtime Rendering一书第七章。

BRDF

前面说过，光照射到物体时会发生一些列作用（反射，折射和吸收）。而对于一般不透明物体，主要是反射和吸收；也就是物体会吸收一部分波长的光，然后反射另一部分波长的光。这种反射特性可以量化为物体表面的材质（Material)。最终的结果是我们看到了一个被照亮的物体。而且物体表面的颜色明显与空间中光的分布和观察者的角度有关。
BRDF函数（Bidirectional Reflection Distribution Function），就是一个描述当光照射到物体表面时有多少光被反射的函数。
上面一节说过，图形学主要关心的是Radiance；这里被反射的光怎么量化呢？其实也就是要计算被反射光的Radiance或者Luminance（L）。而从上一节分析可知，它取决于观测角度和入射光线照度。表面某一点的特定观察角度的被反射光的Radiance除以入射光线照度，应该是一个和物体材质有关的常量系数：

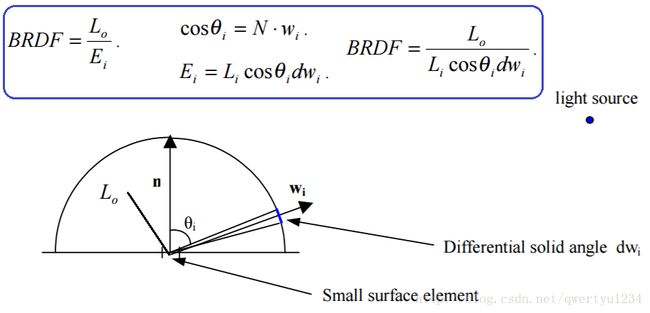
BRDF一般有6个参数，如图所示：

u,v是物体表面坐标，也就是texture采样的坐标。图形学里很多时候使用的是位置无关的BRDF函数；也就是这种材质反射特性是一致的。而实际的物体一般反射特性和位置有关，不同表面区域可能不同，比如木头。一种解决这个问题的办法是引入表面纹理。
有了BRDF函数，我们就有了反射光亮度计算公式：

这里只是粗略提了一下BRDF，后面会详细讲讲这个东西。这个函数其实是现在图形学光照模型里的核心内容之一了。