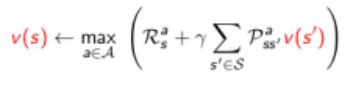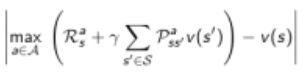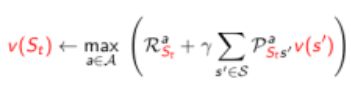动态规划是强化学习里面最基础的部分,其核心思想----通用策略迭代(Generalized Policy Iteration,GPI)。
首先强调一点,动态规划(Dynamic Programming)要求一个完全已知的环境模型,所谓完全已知,就是MDP的五元组全部已知,当然了,主要还是指状态转移概率已知。这种学习方式就是有模型学习(Model-based learning)。
这里我的疑问还是两个。
1.动态规划和前面的有什么联系?
答:强化学习前面已经说过,是一种序列决策问题,一开始不清楚环境的工作方式,不知道执行什么动作是对的,什么是错的,然后就只好不断的在环境试错,进而发现一个好的策略。同样,规划(planning)也属于序列决策问题,不同的是规划的环境是已知的,比如游戏的规则已知等,那么agent就不需要靠与环境的交互来获取下一个状态了,而是知道自己执行某个动作后的状态是什么,然后再优化自己的策略。这两者是不一样的。
动态规划可以将一个复杂问题分为一系列简单的子问题,一旦解决了这些简单的子问题,再将这些子问题的解结合起来就变成复杂问题的解了,并且同时将它们的解保存起来,如果下次遇到相同的子问题,就不用重新计算了。动态规划本质上就是一种环境模型已知的规划方法(planning)。
2.动态规划到底是干什么的?
动态规划的“动态”,指的是某个问题由序列化状态组成,状态的转换是step-by-step进行的。因此,可以step-by-step解决问题。“规划”就是优化子问题。上一节我们提到,通过Bellman方程MDP被递归的切分成子问题,同时它有值函数,保存了每一个子问题的解,因此它能通过动态规划来求解。针对MDP,切分成的子问题就是在每个状态下应该选择的action是什么,MDP的子问题是以一种递归的方式存在,这一时刻的子问题取决于上一时刻的子问题选择了哪个action。
动态规划简单说可以分为两部分,一是预测(prediction),也就是已知MDP的状态、动作、奖励、转移概率、折扣因子和策略,求出每一个状态下的值函数,也就是每个状态下能获得的reward是多少。第二就是控制,什么意思呢,就是在前面的状态、动作等等都已知,但策略未知的情况下,计算出最优的值函数,并且借此计算出最优的策略。动态规划的目的就是完成上面的两件事。适用于动态规划的问题,一般状态转移矩阵都是已知的,简单说就是环境模型已知了,这个时候就可以看做planning问题了。
那么,动态规划解决问题的方法呢,就是GPI,也就是策略迭代、策略评估、策略迭代、策略评估.....知道策略收敛至最优。
1.策略迭代Policy Iteration
怎么迭代呢?先有值,然后改进,再估计值,再改进.....这就是迭代。具体说就是:
策略评估policy evaluation:基于当前的policy计算出每个状态的值函数。
策略改进policy improvement:基于当前的值函数,利用贪心算法找到当前最优的policy。
迭代公式为:\[{v_{k + 1}}(s) = \sum\limits_{a \in A} {{\rm{\pi }}(a|s)(R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{v_k}(s')} )} \]
用语言描述上式就是:对于一次迭代,状态s的价值等于前一次迭代该状态的即时奖励与所有s的下一个可能状态s’的价值与其概率成绩的和。
矩阵形式表示就是:\[{{\bf{v}}^{k + 1}} = {{\bf{R}}^{\rm{\pi }}} + \gamma {{\bf{P}}^{\rm{\pi }}}{{\bf{v}}^k}\]
下面以grid world为例来说明上面式子是如何运用的:
已知条件:
状态空间S:如图所示,S1-S14均为非终止状态,ST为终止状态,就是灰色方格所示两个位置。
动作空间A:{上,下,左,右}对于任何非终止状态可以进行四个方向的动作。
转移概率P:任何试图离开方格世界的动作,其位置将不会发生变化,也就是所谓的在边界执行向外的动作时,位置不变,其余条件下将以1的概率转移到动作指定的状态。(这里肯定是概率为1了,因为规则指制定的很明确,动作会直接跳转下一个位置。但其他MDP问题则不一定啊,比如执行一个动作后,可能会面临多个状态,这时候对于执行完动作后下一个可能的状态就会有一个概率)。
即时奖励R:任何在非终止状态间的转移得到的即时奖励均为-1,进入终止状态的即时奖励为0.
衰减系数γ:1.
当前策略π:Agent初始采取随机行动策略,在任何一个非终止状态下有均等的几率采取任一方向的移动动作。
问题:评估在这个方格世界里给定的策略。
这个问题就等同于:求解该方格世界在给定策略下的状态价值问题,也就是求解在给定策略下该方格世界里每一个状态的价值。
上面介绍的就是值迭代的全部过程,通过已知的模型,对全局状态对应的值函数进行迭代更新,在不需要实际一次一次尝试的情况下,只根据模拟运算迭代,就可以借助值函数评估,利用贪婪策略获得执行动作的最优策略,如果迭代次数足够多的情况下,可以得到一个近似收敛的全部状态的值函数表,就像上图最后一个所示。
上面是一个基本的策略评估过程,没有进行策略改进,主要是因为这个问题太简单了,策略在第3次迭代就已经收敛到最优状态了,没有必要进行策略改进了。
但实际上,更多的问题在长时间的值迭代后,策略收敛并不明显,这个时候,我们该怎么做呢?先状态值函数估计一段时间,然后看看策略怎么样,根据各个状态的值函数,给出一个相对比初始随机要好一点的策略,然后根据这个策略再次进行值函数评估,经过一段时间迭代后,继续调整策略,如此反复,直至最终策略收敛。这就是策略迭代的思想。
根据上面的内容,总结一下,什么是策略迭代呢?策略迭代就是在当前策略上迭代计算v值,再根据v值贪婪地更新策略,如此反复多次,最终得到最优策略π*和最优状态价值函数V*。这里需要说明一下,贪婪的意思就是指仅采用某个动作,这个动作使得状态价值得到最大的行为。下面放上那两个经典的示意图。
上图已经清晰地说明了策略迭代的含义,那么,问题来了,很多时候,策略的更新收敛速度会比状态价值函数值的收敛速度快很多,那么这个时候,还有必要一定要迭代计算直到状态价值得到收敛吗?因为这个时候策略早已经收敛了啊,继续迭代值函数是不是一种资源浪费呢?
答:当然没有必要继续迭代了,我们需要的就是最优策略,至于状态的最优值函数,则根据需求确定是否继续迭代,以及迭代到什么程度。当不需要持续迭代至最优价值函数时,我们可以设置一些条件提前终止迭代,比如设定一个e,比较两次迭代的价值函数平方差,小于e即可;此外,还可以直接设置迭代次数;或者说每迭代一次就更新一次策略。这就是修饰过的策略迭代,英文是Modified Policy Iteration.
2.价值迭代Value Iteration
有了策略迭代,就肯定有价值迭代了。先介绍一下基本定理。
优化原则:一个最优策略可以被分解为两部分,一部分从状态s到下一个s’采取了最优行为A*,另一部分就是在状态s’时遵循一个最优策略。
定理:一个策略能够使得状态s获得最优价值,当且仅当:对于从状态s可以到达的任何状态s’,该策略能够使得状态s’的价值是最优价值:\[{v_*}(s) \leftarrow \mathop {\max }\limits_{a \in A} R_s^a + \gamma \sum\limits_{s'} {P_{ss'}^a{v_*}(s')} \]
确定性价值迭代
在前一个定理的基础上,如果我们清楚地知道我们期望的最终(goal)状态的位置以及反推需要明确的状态间关系,那么可以认为是一个确定性的价值迭代。此时,我们可以把问题分解成一些列的子问题,从最终目标状态开始分析,逐渐往回推,直至推至所有状态。
价值迭代,从初始状态价值开始同步迭代计算,最终收敛,整个过程中没有遵循任何策略。与策略迭代不同,在值迭代过程中,算法不会给出明确的策略,迭代过程其间得到的价值函数,不对应任何策略。价值迭代虽然不需要策略参与,但仍然需要知道状态之间的转移概率,也就是需要知道模型。
最后,再说回来,动态规划的两个问题:预测和控制。预测问题就是在给定策略下迭代计算各个状态的价值函数,控制问题就是通过策略迭代,先给定或随机策略下计算状态价值函数,根据状态函数贪婪更新策略,多次反复找到最优策略。此外,单纯的价值迭代,全程没有策略参与也能获得最优策略,但需要知道状态转移矩阵,即状态s在行为a后到达的所有后续状态及概率。
接下来,说一下复杂度问题,使用状态价值函数或者行为价值函数两种价值迭代的算法时间复杂度都较大,为O(mn2)或者O(m2n2).一种改进方案是使用异步动态规划,其他方法即放弃使用动态规划。
3.动态规划的一些扩展
异步动态规划
a.原位动态规划(In-place dynamic programming):直接原地更新下一个状态的v值,而不像同步迭代那样需要额外存储新的v值。在这种情况下,按何种次序更新状态价值有时候会比较有意义。
b.重要状态有先更新(Priortised Sweeping):对那些重要的状态有先更新。这个时候可以使用Bellman error来确定哪些状态是比较重要的。Bellman error反映的是当前状态价值与更新后的状态价值差的绝对值。Bellman error越大,越有必要优先更新。对那些Bellman error较大的状态进行备份,这种算法使用优先级队列能够较得到有效的实现。
c.real-time programming:更新那些仅与个体关系密切的状态,同时使用个体的经验来知道更新状态的选择。有些状态虽然理论上存在,但在现实中几乎不会出现,利用已有现实经验。
采样更新Sample Backups
动态规划使用full-width backups。意味着使用DP算法,对于每一次状态更新,都要考虑到其所有后继状态及所有可能的行为,同时还要使用MDP中的状态转移矩阵、奖励函数(信息)。DP解决MDP问题的这一特点决定了其对中等规模(百万级别的状态数)的问题较为有效,对于更大规模的问题,会带来Bellman维度灾难。因此在面对大规模MDP问题是,需要寻找更加实际可操作的算法,主要的思想是Sample Backups,后续会详细介绍。这类算法的优点是不需要完整掌握MDP的条件(例如奖励机制、状态转移矩阵等),通过Sampling(举样)可以打破维度灾难,反向更新状态函数的开销是常数级别的,与状态数无关。
近似动态规划(Approximate Dynamic Programming)
使用其他技术手段(例如神经网络)建立一个参数较少、消耗计算资源较少、同时虽然不完全精确但却能够用的近似价值函数。
本节内容主要还是以理解基本概念为主,在实际中很少用动态规划来解决大规模强化学习问题。但ADP用来发文章,尤其是控制领域,近几年来还是非常好的。
参考文献
[1]. Reinforcement learning: an introduction.2017 Draft.
[2].http://www.cnblogs.com/steven-yang/p/6493328.html
[3].http://blog.csdn.net/zz_1215/article/details/44138843
[4].http://chenrudan.github.io/blog/2016/06/17/reinforcementlearninglesssion3.html