自动驾驶之车辆运动学与动力学模型

1. 车辆运动学模型：

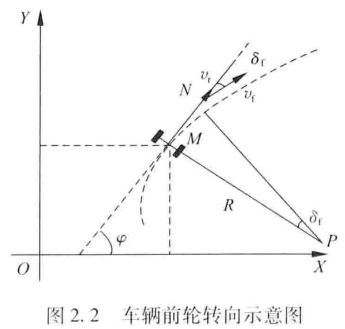
车辆转向运动模型如图$2.1$所示。

在惯性坐标系$OXY$下,

• $\left(X_r,Y_r\right)$和$\left(X_f,Y_f\right)$分別为车辆后轴和前轴轴心的坐标;
• $\phi$为车体的横摆角(航向角);
• ${\delta }_{\mathrm{f}}$为前轮偏角;
• $v_{\mathrm{r}}$为车辆后轴中心速度;
• $v_{\mathrm{f}}$为车辆前轴中心速度;
• $l$为轴距(注意,变量下标$f$代表 front—前,$r$代表rear—后,下同);

图2.2原图：

便于理解：

图2.2所示为车辆转向过程示意图,$R$为后轮转向半径,$P$为车辆的瞬时转动中心,$M$为车辆后轴轴心,$N$为前轴轴心。此处假设转向过程中车辆质心侧偏角保持不变,即车辆瞬时转向半径与道路曲率半径相同。

在后轴行驶轴心$\left(X_r,Y_r\right)$处，速度为：
$$v_r={\dot{X}}_r\cos \phi +{\dot{Y}}_r\sin \phi \text{\hspace{1em}(1)}$$
前后轴的运动学约束为：
$$\{\begin{array}{l}{\dot{X}}_f\sin \left(\phi +{\delta }_f\right)-{\dot{Y}}_f\cos \left(\phi +{\delta }_f\right)=0\\ {\dot{X}}_r\sin \phi -{\dot{Y}}_r\cos \phi =0\end{array}\text{\hspace{1em}(2)}$$
由式(1)和式(2)联合可得：
$$\{\begin{array}{l}{\dot{X}}_r=v_r\cos \phi \\ {\dot{Y}}_r=v_r\sin \phi \end{array}\text{\hspace{1em}(3)}$$

式3推导：将式1等式两边同时乘以$\cos \phi$，然后将式2代入可得式3

根据前后轮的几何关系可得：
$$\{\begin{array}{l}{X}_{\mathrm{f}}=X_r+l\cos \phi \\ Y_{\mathrm{f}}=Y_r+l\sin \phi \end{array}\text{\hspace{1em}(4)}$$
根据式2，式3和式4可得车辆横摆角速度$\omega$为：
$$\omega =\frac{v_r}{l}\tan {\delta }_f\text{\hspace{1em}(5)}$$

式5推导：对式4左右求导：
$$\begin{array}{l}{\dot{X}}_f={\dot{X}}_r+l(-\sin \phi )\cdot \dot{\phi }=V_r\cos \phi +l(-\sin \phi )\cdot \dot{\phi }\\ {\dot{Y}}_f={\dot{Y}}_r+l\cos \phi \cdot \dot{\phi }=V_r\cdot \sin \phi +l\cos \phi \cdot \dot{\phi }\end{array}$$
所以：
$$\begin{array}{rl}& \left(V_r\cos \phi -l\sin \phi \cdot \dot{\phi }\right)\sin \left(\phi +{\delta }_f\right)-\left(V_r\cdot \sin \phi +l\cos \phi \cdot \dot{\phi }\right)\cdot \cos (\phi +{\delta }_f)=0\\ & \begin{array}{r}{V}_r\cos \phi \sin (\phi +{\delta }_f)-V_r\sin \phi (\cos \phi +{\delta }_f)-l\sin \phi \cdot \dot{\phi }\sin (\phi +{\delta }_f)-l\cos \phi \cdot \dot{\phi }\cos (\phi +{\delta }_f)=0\end{array}\end{array}$$
积化和差公式可得：
$$\begin{array}{rl}& V_r\cdot \sin {\delta }_f=l\cdot \dot{\phi }\cdot \cos {\delta }_f\\ & V_r\cdot \tan {\delta }_f=l\cdot \dot{\phi }\\ & \frac{V_x}{l}\cdot \tan {\delta }_f=\omega \end{array}$$

同时由和车速可得到转向半径和前轮偏角：
$$\{\begin{array}{l}R=v_{\mathrm{r}}/\omega \\ {\delta }_f=\arctan (l/R)\end{array}\text{\hspace{1em}(6)}$$
由式(3)和式(5)可得到车辆运动学模型为:
$$\left[\begin{array}{c}{\dot{X}}_{\mathrm{r}}\\ {\dot{Y}}_{\mathrm{r}}\\ \dot{\phi }\end{array}\right]=\left[\begin{array}{c}\cos \phi \\ \sin \phi \\ \tan {\delta }_f/l\end{array}\right]v_{\mathrm{r}}\text{\hspace{1em}(7)}$$
该模型可被进一步表示为更为一般的形式:
$${\dot{\xi }}_{\mathrm{k}\mathrm{i}\mathrm{n}}=f_{\mathrm{k}\mathrm{i}\mathrm{n}}\left({\mathbf{\xi }}_{\mathrm{k}\mathrm{i}\mathrm{n}},{\mathbf{u}}_{\mathrm{k}\mathrm{i}\mathrm{n}}\right)\text{\hspace{1em}(8)}$$
其中,状态量${\mathbf{\xi }}_{\mathrm{k}\mathrm{i}\mathrm{n}}={\left[X_r,Y_r,\phi \right]}^{\top }$,控制量${\mathbf{u}}_{\mathrm{k}\mathrm{i}\mathrm{n}}={\left[v_r,{\delta }_f\right]}^{\mathrm{T}}$。在无人驾驶车辆的路径跟踪控制过程中,往往希望以$\left[v_r,\omega \right]$作为控制量,将式(5)代人式(7)中,该车辆运动学模型可以被转换为如下形式:
$$\left[\begin{array}{c}{\dot{X}}_{\mathrm{r}}\\ {\dot{Y}}_{\mathrm{r}}\\ \dot{\phi }\end{array}\right]=\left[\begin{array}{c}\cos \phi \\ \sin \phi \\ 0\end{array}\right]v_{\mathrm{r}}+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\omega \text{\hspace{1em}(9)}$$

2. 车辆动力学模型：

车辆整车动力学模型一般包括用于分析车辆平顺性的质量-弹簧一阻尼模型和分析车辆操纵稳定性的车辆一轮胎模型。

两者研究的侧重点不同。平顺性分析的重点是车辆的悬架特性,而车辆操纵稳定性分析的重点是车辆纵向及侧向动力学特性。

研究目标是使车辆快速而稳定地跟踪期望路径,属于车辆操纵稳定性问题,因此对于悬架特性不做深入探究;

同时,本书所建立的动力学模型主要是作为模型预測控制器中的预測模型使用,需要在较为准确地描述车辆动力学过程的基础上尽可能进行简化,以减少控制算法的计算量。

综合上述分析,在进行车辆动力学建模时,进行以下理想化的假设：

1. 假设无人驾驶车辆在平坦路面上行驶,忽略车辆垂向运动。
2. 悬架系统及车辆是刚性的,忽略悬架运动及其对耦合关系的影响。
3. 只考虑纯侧偏轮胎特性,忽略轮胎力的纵横向耦合关系。
4. 用单轨模型来描述车辆运动,不考虑载荷的左右转移。
5. 假设车辆行驶速度变化缓慢,忽略前后轴的载荷转移。
6. 忽略纵向和横向空气动力学。

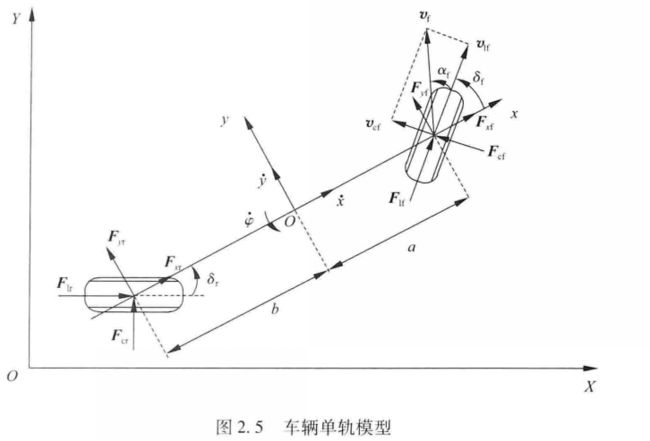
2.1 车辆单轨模型：

基于以上6点理想假设,平面运动车辆只具有3个方向的运动,即纵向、横向和横摆运动。设定车辆为前轮驱动。

满足以上设定的平面运动车辆单轨模型如图2.5所示。其中,坐标系$oxyz$为固定于车身的车辆坐标系。$xoz$处于车辆左右对称的平面内,车辆质心所在点为坐标原点$O$,$x$轴为沿车辆纵轴,$y$轴与车辆纵轴方向垂直,而$z$轴满足右手法则,垂直于$xoy$且向上。坐标系$OXY$为固定于地面的惯性坐标系,也满足右手法则。

图2.5中关于轮胎受力定义如下:

• ${\mathbf{F}}_{\mathrm{l}\mathrm{f}},{\mathbf{F}}_{\mathrm{l}\mathrm{r}}$:前、后轮胎受到的纵向力。
• ${\mathbf{F}}_{\mathrm{e}\mathrm{f}},{\mathbf{F}}_{\mathrm{e}\mathrm{r}}$:前、后轮胎受到的侧向力。
• ${\mathbf{F}}_{\mathrm{x}\mathrm{f}},{\mathbf{F}}_{\mathrm{x}\mathrm{r}}$:前、后轮胎受到的$x$方向的力。
• ${\mathbf{F}}_{\mathrm{y}\mathrm{f}},{\mathbf{F}}_{\mathrm{y}\mathrm{r}}$:前、后轮胎受到的$y$方向的力。

根据牛顿第二定律,分别得沿$x$轴、$y$轴和绕$z$轴的受力平衡方程。

在$x$轴方向上：(其中，乘以2是因为有两个前轮两个后轮)
$$m\ddot{x}=m\dot{y}\dot{\phi }+2{\mathbf{F}}_{xf}+2{\mathbf{F}}_{xr}\text{\hspace{1em}(10)}$$

其中，$ \dot{y} \dot{\varphi}$项是速度乘以角速度得加速度；再乘以质量$ m\dot{y} \dot{\varphi}$表示力；

方向：右手螺旋定则可以得出角速度方向垂直向上（角速度的方向和运动平面垂直），然后角速度$ \dot{\varphi}$叉乘速度$ \dot{y}$右手螺旋定则得到加速度方向沿$x$负方向；然后因为惯性力与速度方向相反所以最终得到惯性力的方向为$x$正方向；

式11同理；

在$y$方向上：
$$m\ddot{y}=-m\dot{x}\dot{\phi }+2{\mathbf{F}}_{yf}+2{\mathbf{F}}_{yr}\text{\hspace{1em}(11)}$$
在$z$轴方向上：
$$I_z\ddot{\phi }=2a{F}_{yf}-2b{F}_{yr}\text{\hspace{1em}(12)}$$
式12中，$a$,$b$分别为质心到前后轴的距离，$m$为车辆质量，$I_z$为车辆绕$z$轴的转动惯量。式12中转动惯量为标量与车辆自身有关，角加速的的方向可以与力矩的方向一致，可以由力矩的方向得到。

轮胎在$x$方向和$y$方向上受到的合力与纵、侧向力的转换关系如下:
$$\begin{array}{l}{F}_{xf}=F_{lf}\cos {\delta }_f-F_{ef}\sin {\delta }_f\end{array}\text{\hspace{1em}(13)}$$

$$F_{xr}=F_{lr}\cos {\delta }_r-F_{er}\sin {\delta }_r\text{\hspace{1em}(14)}$$

$$F_{yf}=F_{lf}\sin {\delta }_f+F_{ef}\cos {\delta }_f\text{\hspace{1em}(15)}$$

$$F_{yr}=F_{lr}\sin {\delta }_r+F_{er}\cos {\delta }_r\text{\hspace{1em}(16)}$$

轮胎的纵向力、侧向力可以表示为轮胎侧偏角、滑移率、路面摩擦系数和垂向载荷等参数的复杂函数:
$${\mathbf{F}}_l=f_l\left(\alpha ,s,\mathbf{\mu },{\mathbf{F}}_z\right)\text{\hspace{1em}(17)}$$

$${\mathbf{F}}_e=f_l\left(\alpha ,s,\mathbf{\mu },{\mathbf{F}}_z\right)\text{\hspace{1em}(18)}$$

式中,$\alpha$为轮胎侧偏角,$s$为滑移率,$\mathbf{\mu }$为路面摩擦系数,${\mathbf{F}}_z$为轮胎所受到的垂向载荷。

轮胎的侧偏角$\alpha$可以由几何关系计算得到:
$$\alpha ={\tan }^{-1}\frac{v_e}{v_l}\text{\hspace{1em}(19)}$$
式中,$v_e$和$v_l$为轮胎在侧向、纵向的速度,可以用坐标系方向的速度$v_x$和$v_y$表示:
$$v_l=v_y\sin \delta +v_x\cos \delta \text{\hspace{1em}(20)}$$

$$v_e=v_y\cos \delta -v_x\sin \delta \text{\hspace{1em}(21)}$$

式中,$\delta$为轮胎偏转角。轮胎的速度往往难以直接获取,一般可以通过车辆速度计算得到。根据图2.5中的速度关系可以推导出以下转换关系:轮胎在地面上的滑移率$s$可以由以下算式计算:
$${\mathbf{v}}_{yf}=\dot{y}+a\dot{\phi }{\mathbf{v}}_{yr}=\dot{y}-b\dot{\phi }\text{\hspace{1em}(22)}$$

$$v_{xf}=\dot{x}{v}_{xr}=\dot{x}\text{\hspace{1em}(23)}$$

22式中，根据质心的速度加上在前后轮的线速度，得到在前后轮出的$y$方向的速度；

轮胎在地面上的滑移率$s$可以由以下算式计算:
$$s=\{\begin{array}{l}1-\frac{r{\omega }_t}{v}\left(v>r{\omega }_t,v\ne 0\right)\\ 1-\frac{v}{r{\omega }_t}\left(v<r{\omega }_t,{\omega }_t\ne 0\right)\end{array}\text{\hspace{1em}(24)}$$
式中,$r$为车轮半径,${\omega }_t$为车轮旋转角速度。

此处与书中原公式有所不同，书中应该是有误的。

假设车辆行驶速度变化缓慢,忽略前后轴的载荷转移,可以通过以下算式计算得到车辆前、后轮胎所受到的垂向载荷:
$$F_{zf}=\frac{bmg}{2(a+b)}\text{\hspace{1em}(25)}$$

$${\mathbf{F}}_{zr}=\frac{amg}{2(a+b)}\text{\hspace{1em}(26)}$$

最后,考虑车身坐标系与惯性坐标系之间的转换关系,可得:
$$\dot{Y}=\dot{x}\sin \phi +\dot{y}\cos \phi \text{\hspace{1em}(27)}$$

$$\dot{X}=\dot{x}\cos \phi -\dot{y}\sin \phi \text{\hspace{1em}(28)}$$

结合式(10)~式(28),可以得到车辆非线性动力学模型。通过算式间的代换,除了路面摩擦系数$\mathbf{\mu }$和滑移率$s$外,其他参数都可以由车辆状态信息计算得到。路面摩擦系数$\mathbf{\mu }$为道路固有信息,给定道路条件后就能获取。把滑移率$s$作为系统的控制量,将有效改善车辆在低附着路面的行驶性能,但对于滑移率的控制本身就是一个复杂的控制问题。因此,假设被控车辆具备良好的防抱死制动系统(ABS),滑移率始终保持在最佳工作点,将系统描述为以下状态空间表达式：
$$\begin{array}{rl}& {\dot{\xi }}_{\mathrm{d}\mathrm{y}\mathrm{n}}=f_{\mathrm{d}\mathrm{y}\mathrm{n}}\left({\mathbf{\xi }}_{\mathrm{d}\mathrm{y}\mathrm{n}},{\mathbf{u}}_{\mathrm{d}\mathrm{y}\mathrm{n}}\right)\\ & {\mathbf{\eta }}_{\mathrm{d}\mathrm{v}\mathrm{a}}=h_{\mathrm{d}\mathrm{y}\mathrm{n}}\left({\mathbf{\xi }}_{\mathrm{d}\mathrm{y}\mathrm{n}}\right)\end{array}\text{\hspace{1em}(29)}$$
在该系统中:

• 状态量选取为${\mathbf{\xi }}_{\mathrm{d}\mathrm{n}\mathrm{n}}={\left[\begin{array}{l}\dot{y},\dot{x},\phi ,\dot{\phi },Y,X\end{array}\right]}^{\top }$
• 控制量选取为${\mathbf{u}}_{\mathrm{d}\mathrm{y}\mathrm{n}}={\delta }_{\mathrm{f}}$(仅考虑前轮转向车辆,${\delta }_{\mathrm{r}}$视为0)
• 输出量选取为${\mathbf{\eta }}_{\mathrm{d}\mathrm{y}\mathrm{n}}={\left[\begin{array}{l}\phi ,Y\end{array}\right]}^{\mathrm{T}}$。

在实际的控制过程中,路面摩擦系数$\mathbf{\mu }$和滑移率$s$视为已知量,该模型即模型预测控制器中预测模型的基础。

2.2 轮胎模型:

在进行车辆动力学仿真时,轮胎所受的垂直力、纵向力、侧向力和回正力矩对汽车的平顺性、操纵稳定性和安全性起着重要作用。由于轮胎结构复杂,动力学性能呈非线性,选择符合实际又便于使用的轮胎模型是建立车辆模型并进行动力学仿真的关键。主要的轮胎模型可以分为理论轮胎模型、经验轮胎模型和物理轮胎模型等。

其中, Pacejka提出的以魔术公式( Magic Formula,MF)为基础的经验轮胎模型,运用三角函数的组合公式拟合轮胎试验数据,描述轮胎的纵向力${\mathbf{F}}_1$,侧向力${\mathbf{F}}_e$。,回正力矩${\mathbf{M}}_z$.,翻转力矩${\mathbf{M}}_x$,阻力矩${\mathbf{M}}_y$,与侧偏角$\alpha$,滑移率$s$之间的定量关系,以及纵向力、侧向力的联合作用工况,能够表达不同驱动情况时的轮胎特性。魔术公式的一般表达式为:
$$Y(x)=D\sin \{\mathrm{Carctan}[Bx-E(Bx-\arctan (Bx))]\}\text{\hspace{1em}(30)}$$
式中,

• 系数$B$,$C$,$D$依次由轮胎的垂直载荷和外倾角确定;$B$为刚度因子;$C$为形状因子;$D$为峰值因子;$E$为曲率因子。$C$为曲线形状因子，决定曲线是侧向力、纵向力还是回正力矩。
• $Y$为输出变量,可以是纵向力${\mathbf{F}}_1$,侧向力${\mathbf{F}}_e$。,回正力矩${\mathbf{M}}_z$.;
• $x$为输入变量,在不同的情况下分別表示轮胎的侧偏角$\alpha$或纵向滑移率$s$;

在实际应用中,由于帘布层转向效应、侧偏力作用或滚动阻力会引起偏移,通常还会引入垂直偏移$S_v$和水平偏移$S_h$(见图2.6)。

Pacejka轮胎模型认为,轮胎在垂直、侧面方向上是线性的,阻尼为常量。这在侧向加速度${\mathbf{a}}_y⩽0.4g$、轮胎侧偏角$\alpha ⩽5^{\circ }$的情景下对常规轮胎具有很高的拟合精度。此外,魔术公式具有较好的健壮性,在极限值以外一定程度内仍可使用,可以对有限工况进行外推且具有较好的置信度。

利用魔术公式计算轮胎的纵向力及侧向力的关系式分別介绍如下：

（1）轮胎纵向力计算方法：

$${\mathbf{F}}_l=D\sin \left[\text{ Carctan }\left(B{x}_{}-E\left(B{x}_{}-\arctan \left(B{x}_{}\right)\right)\right)\right]+S_{\mathrm{v}}\text{\hspace{1em}(31)}$$

式中，

• $x=s+S_h$,$s$为纵向滑移率（负值出现在制动态，-100表示车轮抱死），$S_h$为曲线的水平方向漂移，$S_h$为曲线的垂直方向漂移。
• $C$为曲线的形状因子,$C=B_0$。
• $D$为曲线峰值因子,表示曲线的最大值,$D=B_1{\mathbf{F}}_z^2+B_2{\mathbf{F}}_z$,其中$F_z$为轮胎受到的垂向载荷。
• $B$为刚度因子,$B=\left(B_3{\mathbf{F}}_z^2+B_4{\mathbf{F}}_z\right)\times {\mathrm{e}}^{-B_5{F}_z}/(C\times D)$。
• $E$为曲线的曲率因子,表示曲线最大值附近的形状,$E=B_6{\mathbf{F}}_z^2+B_7{\mathbf{F}}_z+B_{\mathrm{g}}$。
• $S_{\mathrm{h}}$为曲线的水平方向漂移:$S_{\mathrm{h}}=B_9{\mathbf{F}}_z+B_{10}$
• $S_{\mathrm{v}}$为曲线的垂直方向漂移:$S_v=0$。

在纯滑移率作用下轮胎的纵向力如图2.7所示。

（2）轮胎侧向力计算方法：

$${\mathbf{F}}_e=D\sin \left[\text{ Carctan }\left(B{x}_{}-E\left(B{x}_{}-\arctan \left(B{x}_{}\right)\right)\right)\right]+S_{\mathrm{v}}\text{\hspace{1em}(32)}$$

式中，

• $x=\alpha +S_h$,$\mathbf{\alpha }$为轮胎侧偏角，$S_h$为曲线的水平方向漂移，$S_v$为曲线的垂直方向漂移。
• $C$为曲线的形状因子,$C=A_0$。
• $D$为曲线峰值因子,表示曲线的最大值,$D=A_1{\mathbf{F}}_z^2+A_2{\mathbf{F}}_z$,其中$F_z$为轮胎受到的垂向载荷。
• $B$为刚度因子,$B=A_3\sin \left(2\arctan \frac{F_z}{A_4}\right)\times \left(1-A_5|\gamma |\right)/(C\times D)$，其中$\gamma$为轮胎外倾角。
• $E$为曲线的曲率因子,$E=A_6{F}_z+A_7$。
• $S_{\mathrm{h}}$为曲线的水平方向漂移:$S_{\mathrm{h}}=A_9{\mathbf{F}}_z+A_{10}+A_8\gamma$。
• $S_{\mathrm{v}}$为曲线的垂直方向漂移:$S_1=A_{11}{F}_z\gamma +A_{12}{F}_z+A_{13}$。

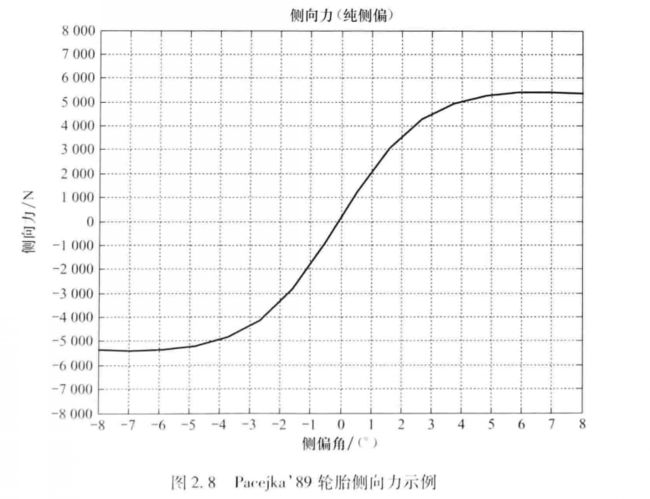
在纯侧偏角作用下轮胎的侧向力如图2.8所示。

（3）轮胎侧向力计算方法：

$${\mathbf{M}}_z=D\sin \left[\text{ Carctan }\left(B{x}_{}-E\left(B{x}_{}-\arctan \left(B{x}_{}\right)\right)\right)\right]+S_{\mathrm{v}}\text{\hspace{1em}(33)}$$

式中，

• 此时$x$为回正力矩计算组合变量，$x=\alpha +S_h$,$\mathbf{\alpha }$为轮胎侧偏角，$S_h$为曲线的水平方向漂移，$S_v$为曲线的垂直方向漂移。
• $C$为曲线的形状因子，回正力矩计算时取$C_0$值,$C=C_0$。
• $D$为曲线峰值因子,表示曲线的最大值,$D=C_1{\mathbf{F}}_z^2+C_2{\mathbf{F}}_z$,其中$F_z$为轮胎受到的垂向载荷。
• $BCD$为回正力矩零点处的扭转刚度,$BCD=\left(C_3{\mathbf{F}}_z^2+C_4{\mathbf{F}}_z\right)\times \left(1-C_6|\gamma |\right)\times e^{-C_5{F}_z}$，其中$\gamma$为轮胎外倾角。
• $B$为刚度因子：$B=BCD/(C\times D)$。
• $E$为曲线的曲率因子,$E=\left(C_7{\mathbf{F}}_z^2+C_8{\mathbf{F}}_z+C_9\right)\times \left(1-C_{10}|\gamma |\right)$。
• $S_{\mathrm{h}}$为曲线的水平方向漂移:$S_h=C_{11}\gamma +C_{12}{F}_z+C_{13}$。
• $S_{\mathrm{v}}$为曲线的垂直方向漂移:$S_v=\gamma \left(C_{14}{F}_z^2+C_{15}{F}_z\right)+C_{16}{F}_z+C_{17}$。

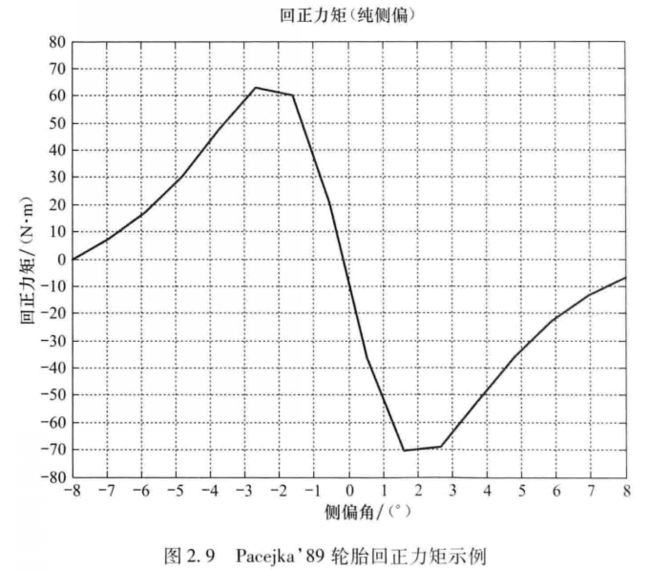
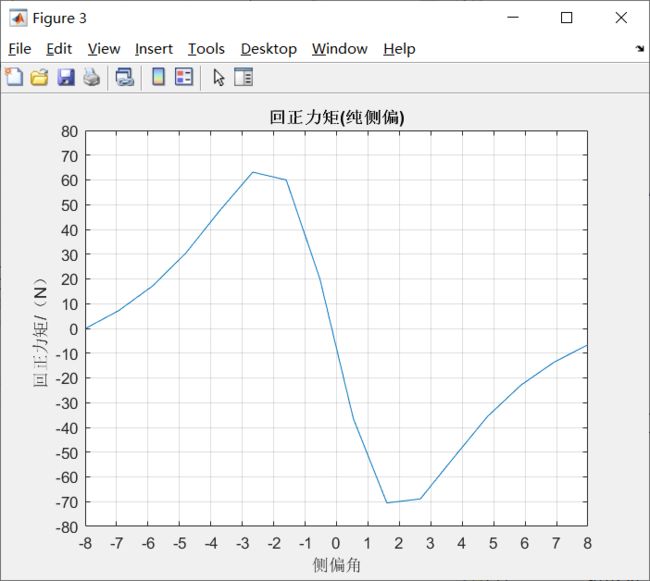
在纯侧偏角作用下轮胎的回正力矩如图2.9所示。

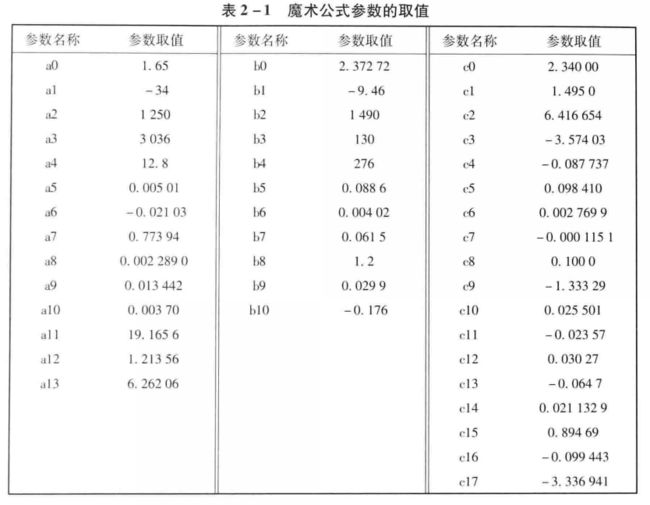
代码实现：轮胎模型matlab代码实现 （代码实现中参数的取值如下表2-1）

执行结果：

2.3 小角度假设下的车辆动力学模型：

通过将式(29)和轮胎模型结合,可以发现建立的非线性状态空间表达式相对于模型预测控制器的设计来说还是过于复杂,因此需要进一步简化。图2.10为根据实验数据所绘制的不同载荷下轮胎纵向力及側向力曲线。

从图2.10中可以看出,在侧偏角及纵向滑移率较小时,轮胎力可以用线性函数近似描述。这在侧向加速度$a_y⩽0.4g$的情况下对常规轮胎具有较高的拟合精度。在这个范围内,用以下算式得到轮胎的纵向力和侧向力：
$$F_l=C_{l}s{F}_e=C_e\alpha \text{\hspace{1em}(34)}$$
式中,$C_l$为轮胎纵向刚度,$C_e$为轮胎侧偏刚度。

在之前所建立的非线性模型中,存在较多的三角函数,对于模型简化有较大的困难。因此,在轮胎力的计算过程中,提出小角速度假设,即满足如下近似条件:
$$\cos \theta \approx \theta ,\sin \theta \approx \theta ,\tan \theta \approx \theta$$
式中,$\theta$表示各个角,包括前轮偏角,前、后轮胎侧偏角等。

通过以上简化并结合式(19)~式(23),可以得到轮胎側偏角的计算关系式:
$${\alpha }_{\mathrm{f}}=\frac{\dot{y}+a\dot{\phi }}{\dot{x}}-{\delta }_{\mathrm{f}}{\alpha }_{\mathrm{r}}=\frac{\dot{y}-b\dot{\phi }}{\dot{x}}\text{\hspace{1em}(35)}$$

之所以后面一项没有减去${\delta }_{\mathrm{r}}$，是因为：(仅考虑前轮转向车辆,${\delta }_{\mathrm{r}}$视为0,书中第25页有提到)

根据式(35)和线性轮胎模型,就可以很容易计算得到轮胎力。

前、后轮胎的侧向力:
$$F_{\mathrm{e}\mathrm{f}}=C_{\mathrm{e}\mathrm{f}}\left({\delta }_{\mathrm{f}}-\frac{\dot{y}+a\dot{\phi }}{\dot{x}}\right)F_{\mathrm{e}\mathrm{r}}=C_{\mathrm{e}\mathrm{r}}\frac{b\dot{\phi }-\dot{y}}{\dot{x}}\text{\hspace{1em}(36)}$$

此处$F_{\mathrm{e}\mathrm{f}}$等式右端的负号可以在系数$C_{\mathrm{e}\mathrm{f}}$中体现，所以相减的顺序可以和上面有所不同。

前、后轮胎的纵向力：
$$F_{lf}=C_{lf}{s}_f{F}_{lr}=C_{lr}{s}_r\text{\hspace{1em}(37)}$$
将以上简化后的结果代入式(29)，即分别代入式（10）式(11)和式(12)后,得到了基于前轮偏角较小和线性轮胎模型假设后的车辆动力学非线性模型:
$$\begin{array}{l}m\ddot{y}=-m\dot{x}\dot{\phi }+2\left[C_{ef}\left({\delta }_{\mathrm{f}}-\frac{\dot{y}+a\dot{\phi }}{\dot{x}}\right)+C_{\mathrm{e}\mathrm{r}}\frac{b\dot{\phi }-\dot{y}}{\dot{x}}\right]\\ m\ddot{x}=m\dot{y}\dot{\phi }+2\left[C_{\mathrm{l}\mathrm{f}}{s}_{\mathrm{f}}+C_{\mathrm{e}\mathrm{f}}\left({\delta }_{\mathrm{f}}-\frac{\dot{y}+a\dot{\phi }}{\dot{x}}\right){\delta }_{\mathrm{f}}+C_{l\mathrm{r}}{s}_{\mathrm{r}}\right]\\ I_z\ddot{\phi }=2\left[a{C}_{\mathrm{e}\mathrm{f}}\left({\delta }_{\mathrm{f}}-\frac{\dot{y}+a\dot{\phi }}{\dot{x}}\right)-b{C}_{\mathrm{e}\mathrm{r}}\frac{b\dot{\phi }-\dot{y}}{\dot{x}}\right]\\ \dot{Y}=\dot{x}\sin \phi +\dot{y}\cos \phi \\ \dot{X}=\dot{x}\cos \phi -\dot{y}\sin \phi \end{array}\text{\hspace{1em}(38)}$$
在该系统中,状态量选取为${\xi }_{\mathrm{d}\mathrm{y}\mathrm{n}}={\left[\begin{array}{l}\dot{y},\dot{x},\phi ,\dot{\phi },Y,X\end{array}\right]}^{\mathrm{T}}$控制量选取为${\mathbf{u}}_{\mathrm{d}\mathrm{y}\mathrm{n}}={\delta }_{\mathrm{f}}$。

参考文献：

无人驾驶车辆模型预测控制 龚建伟等著

汽车的横摆角速度

惯性力

角速度方向判断

角加速度的方向可以与力矩的方向相同，可以有力矩方向得到

力矩图

力矩

滑移率

滑移率百科

魔术公式百科