迷宫问题解决方法：分别基于深度搜索和广度搜索的思想来实现

        本文针对迷宫问题，探讨解决思路并给出实现代码。在本文中，采用的图的深度优先搜索和广度优先搜索两种方法分别对迷宫的路径进行了求解。

        首先来看迷宫问题的描述，可以参考此处，简而言之就是，通过一个二维数组（int型）来表示迷宫，迷宫中0表示可行，1表示不可行。在本文的实现中，可以输入给定迷宫，定义迷宫入口和出口，并查找迷宫路径。

        总体的描述：在本文中，定义了结构体Node，用于存放节点信息，而Node内只有两个变量，标识节点的行坐标与列坐标。定义了迷宫类maze，并分别定义了相应的get、set函数，输入显示迷宫的函数，以及迷宫路径求解，路径打印的函数等，在下文代码会分别看到。最后，编写了简单的测试样例，来对以上的实现进行测试。

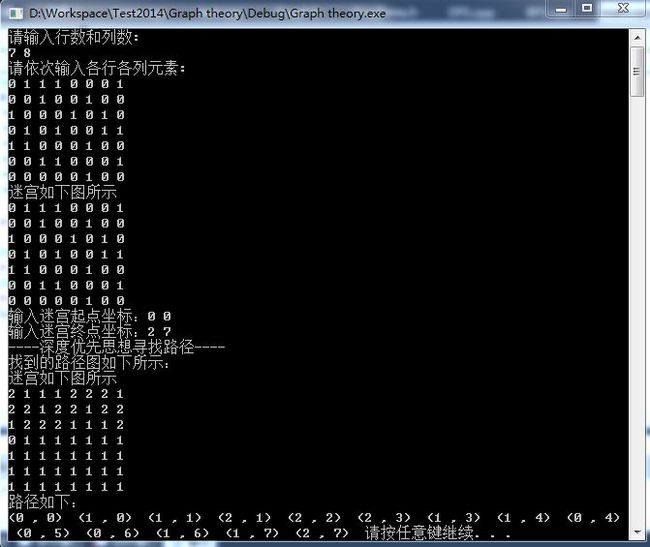
        深度优先搜索的思想：对于深度优先搜索解决迷宫问题的思想，在于从起始点开始，沿着某一可行的方向进行探寻，若在新的坐标点之后仍能继续前进，则继续前进，直到找到所求的结束点；若当前点前行遇到阻碍（意即除了它的上一点的方向之外，其余的四个方向都不可行），则采取回溯方法，回溯到上一个点，并将该点标记为不可行，再继续在回溯的顶点上探寻可行的方向，如此重复，知道找到结束点。基于以上分析可以发现，对于每个点，需要知道当它不可行时退回到哪个点，故而需要记录其上一个点甚至是已经走过的路线的路径，在此处可以通过栈来加以存储记录。每前进到下一个点，就将该点加入栈中，若某点不可行，则弹出栈顶元素（即当前点），然后获得此时的栈顶元素（即上一个点）在进行探寻，到最后，若路径存在，栈中的点则为路径的所有点，切起始点在栈底，而结束点在栈顶。

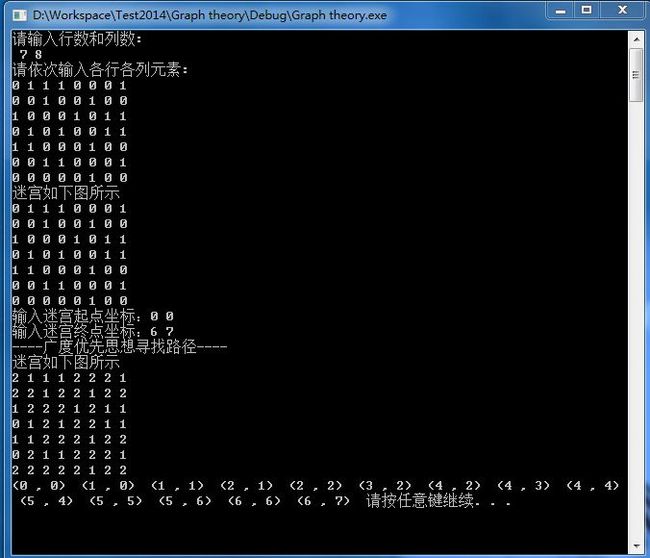
        对于广度优先搜索的思想，也是类似。只是广度优先搜索的思想是从起始点开始，将其所有的邻接顶点均放入队列，每次从队列头取元素，检查其是否是结束点，若不是，则将其所有未被访问过的邻接顶点加入队列中。由于队列并不像堆栈一样保留了所有经过的点，故而本文中采用二维数组 pre来存放每个点的上一个点的位置，在初始时设置pre的所有点的上一个点坐标为（-1，-1）以示其未被访问。在最后，若存在路径，则从pre的终点位置依次倒退上一个点知道起始点即可。

       下面给出示例代码：在本代码的实现中，迷宫的行列以及各个点的内容均由操作者输入，同时起始点与结束点也是有操作者设定的，增加了一定的操作性。

/*迷宫问题，深度优先搜索和广度优先搜索的思路分别解决。
*FileName: maze.cpp
*----By F8Master
*/

#include
#include
#include
using namespace std;

const int defaultRowAccount = 30;
const int defaultColAccount = 30;

struct Node //节点结构体定义
{
	int rowNum;//节点坐标行列号
	int colNum;
};

class Maze
{
public:
	Maze(int r=defaultRowAccount,int c =defaultColAccount);
	~Maze(){delete []node;}
	int getRow(){return rowAccount;} //以下几个分别获得或设置行列以及节点信息
	int getCol(){return colAccount;}
	void setRow(int r){rowAccount = r;}
	void setCol(int c){colAccount = c;}
	int getNode(Node n){return node[n.rowNum][n.colNum];} //参数为点
	int getNode(int i,int j){return node[i][j];} //函数重载，参数为点的横纵坐标
	void setNode(Node n,int value){node[n.rowNum][n.colNum]=value;}
	void setNode(int i,int j,int value){node[i][j] = value;}//函数重载，前两个参数为点的横纵坐标
	void drawMaze();//依据输入构造迷宫
	void printMaze();//画出迷宫
	void dealMaze(stack &s ,Node &sNode,Node &eNode);//深搜的思路找迷宫路径
	void dealMaze(Node &sNode,Node &eNode,Node **pre);//函数重载。广搜的思路找迷宫路径
	void printRoute(stack &s); //深度搜索之后打印路径
	void printRoute(Node **pre ,Node start,Node end);//函数重载。广度优先搜索之后打印路径
private:
	int **node; //存放迷宫的数组
	int maxRowAccount;
	int maxColAccount;
	int rowAccount;//迷宫中行数
	int colAccount;//列数
};

Maze::Maze(int r,int c ){ //构造函数
	rowAccount = 0;
	colAccount = 0;
	maxRowAccount = defaultRowAccount;
	maxColAccount = defaultColAccount;
	node = new int *[maxRowAccount];//node初始化
	for(int i =0;i>i>>j;
	this->setRow(i);
	this->setCol(j);
	cout<<"请依次输入各行各列元素:"<>k;
			temp.rowNum = i;
			temp.colNum = j;
			this->setNode(temp,k);
		}
}
void Maze::printMaze()
{
	cout<<"迷宫如下图所示"< &s ,Node &sNode,Node &eNode)//参数依次为存储路径所用的栈，起始点横纵坐标，结束点横纵坐标
{
	cout<<"----深度优先思想寻找路径----"<getRow();
	int colAll = this->getCol();
	Maze deal;//用于记录并解决问题的迷宫图，会实时修改
	deal.setRow( rowAll);
	deal.setCol( colAll);
	for(int i = 0;igetNode(temp));
		}

	node.rowNum = sNode.rowNum;
	node.colNum = sNode.colNum;
	s.push(node);
	deal.setNode(node,instack);//改变标记，表明该点已经访问过

	while(!s.empty())//注意此方法由于探寻方向的顺序固定，故找到的不一定是最佳路径，只是可行路径
	{
		node = s.top();
		/*cout<<"\n弹出点："<<"("<0 && deal.getNode(node.rowNum-1,node.colNum)==access)//向上可行
		{
			node.rowNum--; 
			s.push(node);
			deal.setNode(node,instack);
		}
		else if(node.rowNum0 && deal.getNode(node.rowNum,node.colNum-1)==access)//向左可行
		{
			node.colNum--;
			s.push(node);
			deal.setNode(node,instack);
		}
		else if(node.colNum q;
	int rowAll = this->getRow();
	int colAll = this->getCol();
	
	Maze deal;//用于记录并解决问题的迷宫图
	deal.setRow( this->getRow());
	deal.setCol( this->getCol());
	temp.rowNum = -1;
	temp.colNum = -1;
	for(int i = 0;igetNode(i,j));
			pre[i][j]=temp;
		}
	node.rowNum = sNode.rowNum;
	node.colNum = sNode.colNum;
	q.push(node);
	deal.setNode(node.rowNum,node.colNum,instack);//改变标记，表明该点已经访问过

	while(!q.empty())
	{
		node = q.front();
		q.pop();
		if(node.rowNum ==eNode.rowNum && node.colNum == eNode.colNum)//找到
		{
			break;
		}
		if(node.rowNum>0 && deal.getNode(node.rowNum-1,node.colNum)==access)//向上可行
		{
		
			temp.rowNum = node.rowNum-1;
			temp.colNum = node.colNum;
			q.push(temp);//邻接未被访问的可行点加入队列
			deal.setNode(temp.rowNum,temp.colNum,instack);//邻接点访问之后改变其标记
			pre[temp.rowNum][temp.colNum] = node;//记录其上一个点的坐标
		}
		if(node.rowNum0 && deal.getNode(node.rowNum,node.colNum-1)==access)//向左可行
		{
			temp.rowNum = node.rowNum;
			temp.colNum = node.colNum-1;
			q.push(temp);
			deal.setNode(temp.rowNum,temp.colNum,instack);
			pre[temp.rowNum][temp.colNum] = node;
		}
		if(node.colNum &s)//深搜之后，打印路径，s中存放了路径的所有点
{
	Node temp;
	stack out;
	if(s.empty())
	{
		cout<<"不存在路径!"< s; 
	Node node = end;
	s.push(node);
	while(node.rowNum!=start.rowNum || node.colNum!=start.colNum)
	{	
		node = pre[node.rowNum][node.colNum];
		s.push(node);
	}
	while(!s.empty())
	{
		node = s.top();
		cout<<"("<s;
	Node startN,endN;
	maze.drawMaze(); //输入迷宫
	maze.printMaze();//显示未经改动的迷宫图

	cout<<"输入迷宫起点坐标：";
	cin>>startN.rowNum>>startN.colNum;
	
	cout<<"输入迷宫终点坐标：";
	cin>>endN.rowNum>>endN.colNum;

	maze.dealMaze(s,startN,endN);//深搜思想解决
	maze.printRoute(s);//打印路径
	
}
void test_Maze_BFS()
{
	Maze maze;
	Node startN,endN;
	Node **pre;
	maze.drawMaze();
	pre = new Node *[maze.getRow()];
	for(int i = 0;i>startN.rowNum>>startN.colNum;

	cout<<"输入迷宫终点坐标：";
	cin>>endN.rowNum>>endN.colNum;

	maze.dealMaze(startN,endN,pre);
	maze.printRoute(pre,startN,endN);
}

下面给出若干测试样例：

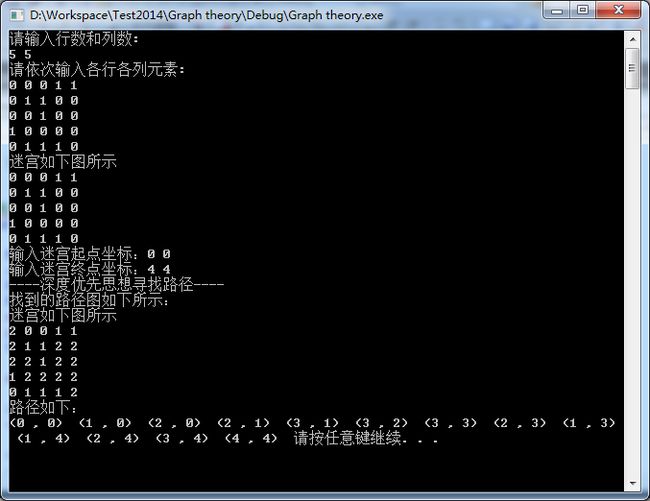
用深度搜索实现5×5迷宫中的搜索（左上角到右下角）：

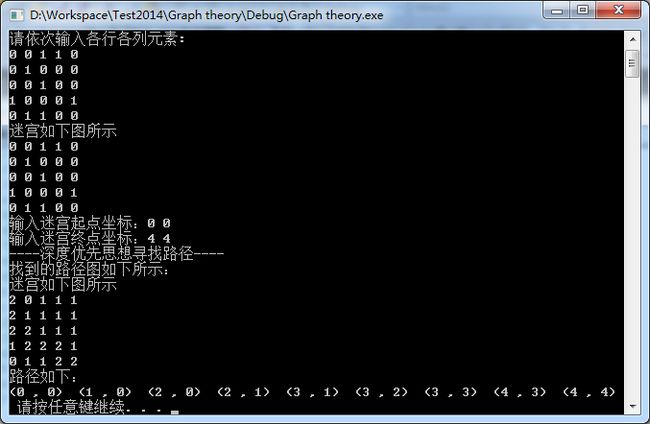
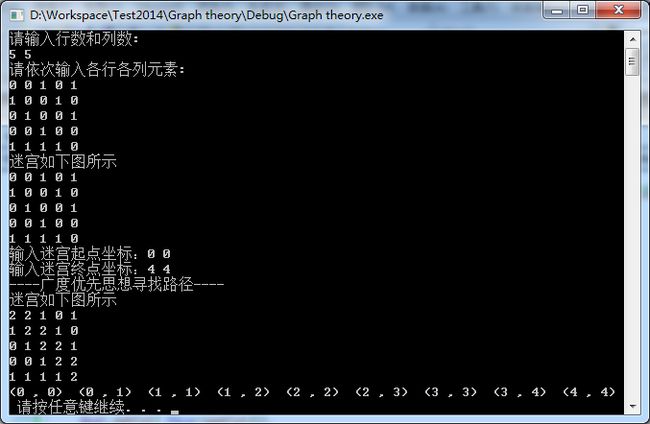
        用广度搜索实现5×5迷宫中的搜索（左上角到右下角）：

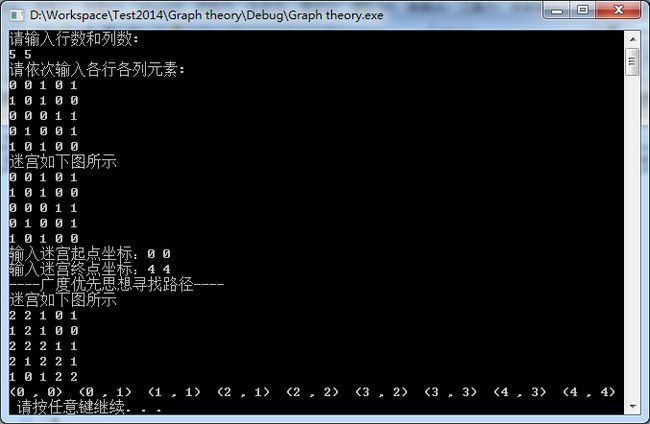
7×8的迷宫中分别找给顶点：

转载于:https://www.cnblogs.com/f8master/p/3826071.html