一招制敌的贪心算法

摘要

本文主要介绍贪心算法。 贪心算法并不是一种特定的算法，而是一种策略，一种一招制敌的策略。每次都贪心选择最好的，就是贪心算法。 所以贪心算法往往效率高，代码短。常见的贪心问题：区间问题， Huffman树等。

区间问题

最大不相交区间数

例题： HDU 2037 今年暑假不AC

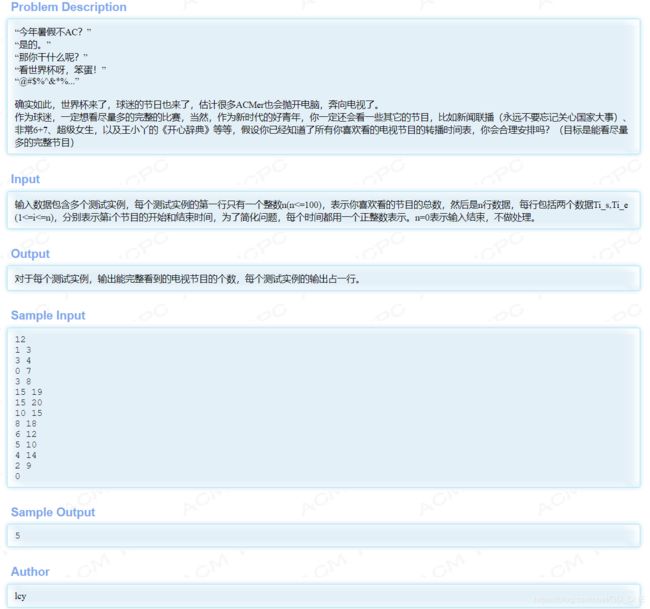
题目大意就是给出n个节目，n个节目起止时间不同，要求选出最多的没有时间冲突的节目。

这道题是一道经典的贪心问题。本质上就是求出最大不相交区间数。对于本题，区间端点可以相交。

做法：对所有节目按结束时间从小到大排序。然后枚举每个区间是否和前一个区间有相交。如果没有，节目数就加一。

C++代码：

#include 
#include 
using namespace std;

struct node{ 
    int l, r;
}arr[100005];

int cmp(node a, node b){
    return a.r < b.r;
}
int main(){
    int n;
    while(cin>>n, n){ 
        int l, r;
        for(int i = 0; i < n; i++){
            cin>>l>>r;
            arr[i].l = l;
            arr[i].r = r;
        }
        
        sort(arr, arr + n, cmp);
        
        int f = -2e9;
        int res = 0;
        for(int i = 0; i < n; i++){
            if(arr[i].l >= f){
                res ++;
                f = arr[i].r;
            }
        }
        cout<<res<<endl;
    }
    return 0;
}

区间覆盖问题

例题 POJ 2376 Cleaning Shifts

题目大意：John有N头牛，每头牛都有不同的工作时间，John将一天分为T个时间段，从1~T。他想让每个时间段都有牛做静洁工作，问最少需要几头牛。

也就说，找出最少的牛，这些牛的工作时间可以覆盖1~T。

做法：将每头牛按工作时间的起始时间从小到大进行排序，然后对于1~T时刻中未被覆盖的时刻中的起始时刻，找出起始时间能覆盖该时刻并且结束时间最晚的牛。

注意本题坑点：本题给出的是时刻而不是区间端点，所以除了第一头牛的开始时间必须是1，此后的第i头牛的起始时间最晚是第i-1头牛的结束时间+1.
例如对于样例：
4 10
1 3
3 5
4 7
8 10
答案是选择[1 3] [4 7] [8 10]

首先，1~T时刻中 1时刻是未被覆盖的时刻中的起始时刻，只有[1 3] 能够覆盖。

然后 4时刻变为未被覆盖的时刻中的起始时刻， 只有[4 7] 能够覆盖4时刻

最后 8时刻变为未被覆盖的时刻中的起始时刻， 只有[8 10] 能够覆盖8时刻

此时1~T时刻已经被覆盖完了，结束。

所以最终答案是 3。

JAVA代码：

import java.io.*;
import java.util.*;
import java.math.*;

public class Main{
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    
    static class node implements Comparable<node>{ //自定义类，保存起止时间
        int l, r;                               //需要按起始时间排序，所以实现Comparable接口，自定义排序。
        node(int l, int r){                   
            this.l = l;
            this.r = r;
        }
        public int compareTo(node b) {
            return this.l - b.l;
        } 
    }
    
    static node[] arr = new node[25005];
    
    static int Int(String s){
        return Integer.parseInt(s);
    }
    
    public static void main(String[] args) throws Exception{
    	
        int T, n;
        String[] s = in.readLine().split(" ");
        n = Integer.parseInt(s[0]);
        T = Integer.parseInt(s[1]);
        
        for(int i = 0; i < n; i++){
        	String[] s1 = in.readLine().split(" ");// 读入
        	arr[i] = new node(Int(s1[0]), Int(s1[1]));
        }
        
        Arrays.sort(arr, 0, n - 1); // 排序
        
        int flag = 0, res = 0, start = 1; // // 刚开始1时刻是未被覆盖的区间的起始时刻
     
        for(int i = 0; i < n; i++){
            int j = i;
			int r = -1000;
            
            if(arr[0].l > 1){
                break;
            }
            while(j < n &&(start != 1 &&arr[j].l <= start+1|| start == 1 && arr[j].l == 1)){
                r = Math.max(r, arr[j].r);
                j ++;
            }
            res ++;
            if(r < start){ // 如果r < start说明没有符合条件的区间。直接break输出-1
                break;
            }
            
            if(r >= T   ){ // 如果 r >= T 说明区间已经被完全覆盖，break输出答案
                flag = 1;
                break;
            }
            
            start = r; // 更新起始时刻
            i = j - 1; // 0 ~ j-1个区间已经遍历过了，直接跳过。
        }
        if(flag != 1) res = -1;
        out.write(Integer.toString(res));
        out.flush();
    }
}

Huffman树

Huffman树也是贪心思想的经典体现，给定n个叶结点，用这n个叶结点构造一个二叉树，Huffman树是带权路径长度最小的二叉树。

Huffman树详解视频：
https://www.bilibili.com/video/BV18t411U7bj/?spm_id_from=333.788.videocard.4

Huffman树的特点：权值越大的叶结点一定距离根节点越近，权值越小的叶节点一定距离根节点越远。

构造Huffman树：
为了保证得到的带权路径长度最小，我们每次都要合并两个最小的叶节点。

例题： POJ 3253

题目大意： John想将一块木板切割成n块，没切割一次，就会发费当前切割的木板总长度的代价，求最小代价。

转化为Huffman树， John最终切成的木块长度就是叶节点。 所以只需要建个Huffman树然后求出带权路径长度就行了。

使用优先队列每次合并两个最小的节点。

代码：

import java.io.*;
import java.util.*;
import java.math.*;

public class Main{
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    
    static int Int(String s){
        return Integer.valueOf(s);
    }
    
    public static void main(String[] args) throws Exception{
    	int n = Int(in.readLine());
       	PriorityQueue<Integer> heap = new PriorityQueue<Integer>(); // 小根堆
    
        while(n --> 0){
            heap.add(Int(in.readLine()));
        }
    	
    	long res = 0;// 答案很大，用long存
    
    	while(heap.size() != 1)
    	{
    	    int min = heap.poll() + heap.poll();
    	    res += min;
    	    heap.add(min);
    	}
    	
    	out.write(res + "");
    	out.flush();
    }
}

还有很多其他类型的贪心问题，文本就不在一一列举，做贪心主要就是看能不能贪对，想不出来怎么贪心就做不对，想出来了代码就很简单，所以还是要多做题。