Apollo进阶课程㉙丨Apollo控制技术详解——控制器的类型
原创： 阿波君 Apollo开发者社区 8月28日
控制主要是为了弥补数学模型和物理世界执行之间的不一致性。对于自动驾驶而言，规划的轨迹和车辆的实际运行轨迹并不完全一致，控制器按照规划轨迹在条件允许下尽可能地调节车辆的运行轨迹。
上周阿波君为大家详细介绍了「进阶课程㉘Apollo控制技术详解——基于模型的控制方法」。
主要介绍Apollo使用基于模型的控制方法，包括四个部分：建模、系统辨识、控制器设计和参数调优。其中详细地讲解了建模的类别、属性以及控制模块中的模型包括运动学模型和动力学模型。此外，还介绍了系统辨识、控制器设计等。
本周阿波君将继续与大家分享Apollo控制技术详解——控制器类型的相关课程。下面，我们一起进入进阶课程第29期。
目录
1.前馈环控制
优化控制
LQR（二次线性调节器）
MPC
鲁棒性控制（Robust Control）
离散化
2.控制器设计的其它方面
3.控制器的发展趋势
4.工程应用案例
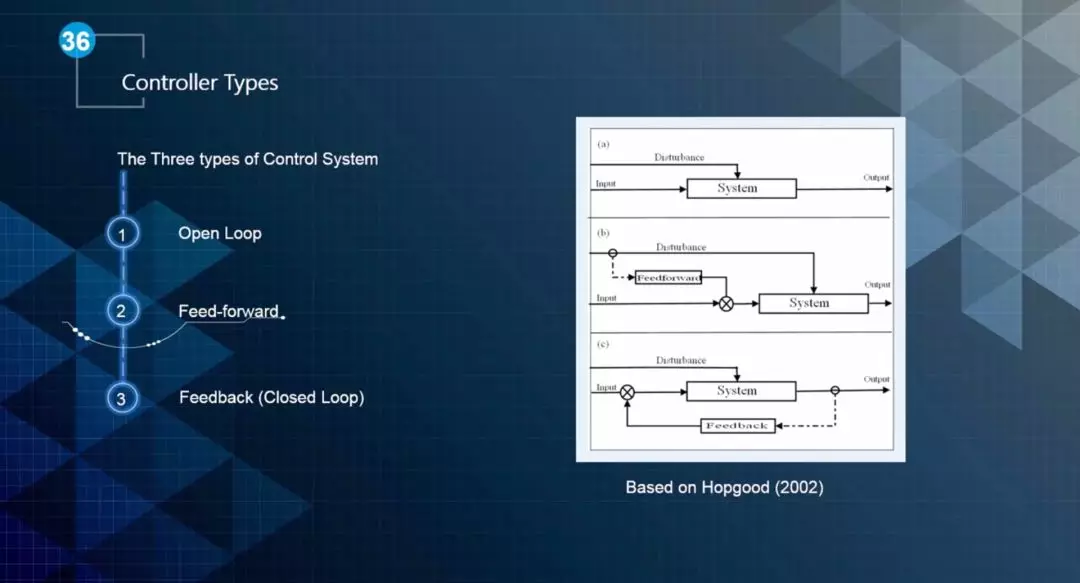
控制器的类型大致可以分为三类，分别是开环控制、前馈环控制和后馈环控制，如图1所示。
▲图1 控制器的类型
1.前馈环控制
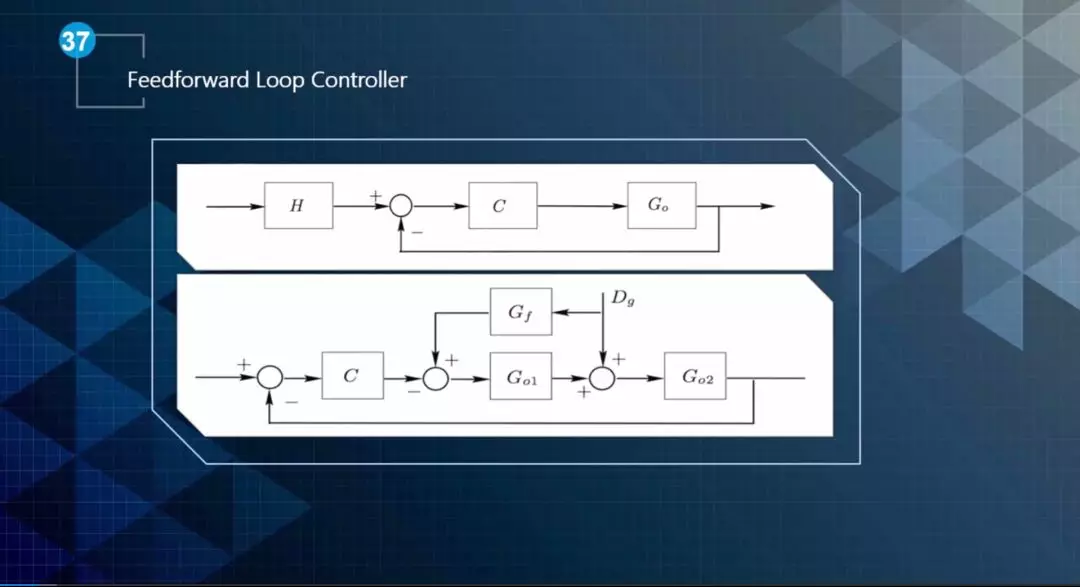
前馈环控制器可以分为两类，如图2所示。上图是增加一个H，可以看出是一个前置滤波器，把输入转化为理想的输入。下图是把扰动量加入到前馈环中，将模型的先验知识添加到环路，减少扰动的影响。
▲图2 前馈环控制器的类别
前馈环控制器的主要控制策略有很多种，这里主要介绍三种，分别是Optimal Control（优化控制）、 Adaptive Control（自适应控制）、Robust Control（鲁棒性控制），如图3所示。
▲图3 前馈环控制的主要控制策略
那么设计控制器的时候需要考虑什么因素呢？首先是可控性和可观性。可控性（Controllability）是指系统是不是能按期望通过控制量U达到相应的动态；可观性（Observability）是指在初识状态已知的情况下，是不是可以重构整个系统的状态，如图4所示。
▲图4 控制器设计考虑可控性和可观性
优化控制
优化控制的目的是在给定系统的情况下，找到或者设计出一个控制法则使系统可以满足特定的优化标准。图5给出了优化控制的一个分类和演化过程。最早可追溯到上世纪五六十年代的卡尔曼滤波和后来的LQR。这两个控制在一起可以得到一个LQG，需要注意的是LQG是一个线性并且没有限制的控制器，在这个基础上增加限制，就得到了LMPC。在LMPC的基础上，增加非线性因素就得到了MPC。从上图左边到右边的控制器演化，响应速度更快，但是计算代价更高。
▲图5 优化控制
LQR（二次线性调节器）
Apollo项目开源了LQR算法，这里简要介绍一下。在线性化的横向状态方程上做LQR，一般的表示方程如图6所示。
▲图6 LQR算法
它的状态空间可以用方程
表示，
是输入，集中最重要是设计代价函数，如图中的第四行所示。首先，代价函数必须是corrected的，是x的二次方的形式。另外，还有两个调节因子，一个是Q，另一个是R。
在这个基础上，增加前馈项，然后做一个拉普拉斯转换，从时域转换到频域。我们的目标是使系统的error X=0，经过一系列变换之后可以算出
，进而得到前馈项，具体过程如图7所示。
▲图7 Controller Design-LQR Controller的求解过程
MPC
MPC控制器的基本逻辑如图8所示。它包含Predictive Plant、Real Plant、MPC Controller以及Feedback Correction。MPC和跟LQR的区别在于，MPC有一个关于时间T的优化矩阵，同时还有一系列的控制约束。如果想设计一个非常高效的、能在工程上应用其满足鲁棒性理论要求的控制器，一定要做离散化。
▲图8 MPC控制器的基本逻辑
MPC的代价函数如图9所示。从图中可以看出，代价函数增加了约束边界，有上边界和下边界。
▲图9 MPC的代价函数
关于优化控制的一些课外阅读，可以参照图10中列出的参考文献。
▲图10 优化控制的相关参考资料
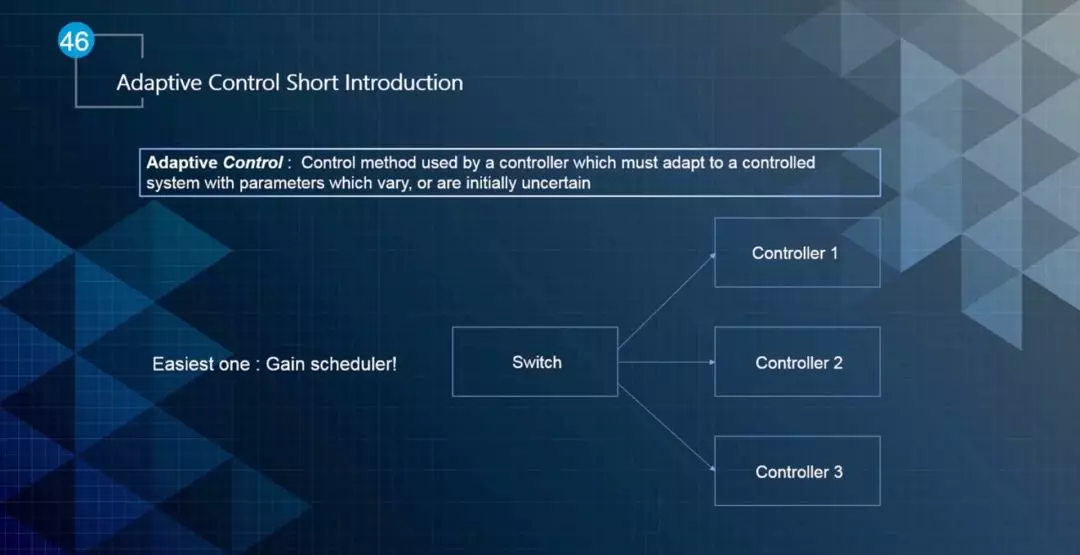
下面简单介绍一下自适应控制和鲁棒性控制。自适应控制是一种针对控制系统中参数多变或者初始值不确定的控制方法。最简单的一种方法就是根据输入使用swith的方式，根据输入或者gain选择不同的控制算法，如下图所示。
▲图11 自适应控制
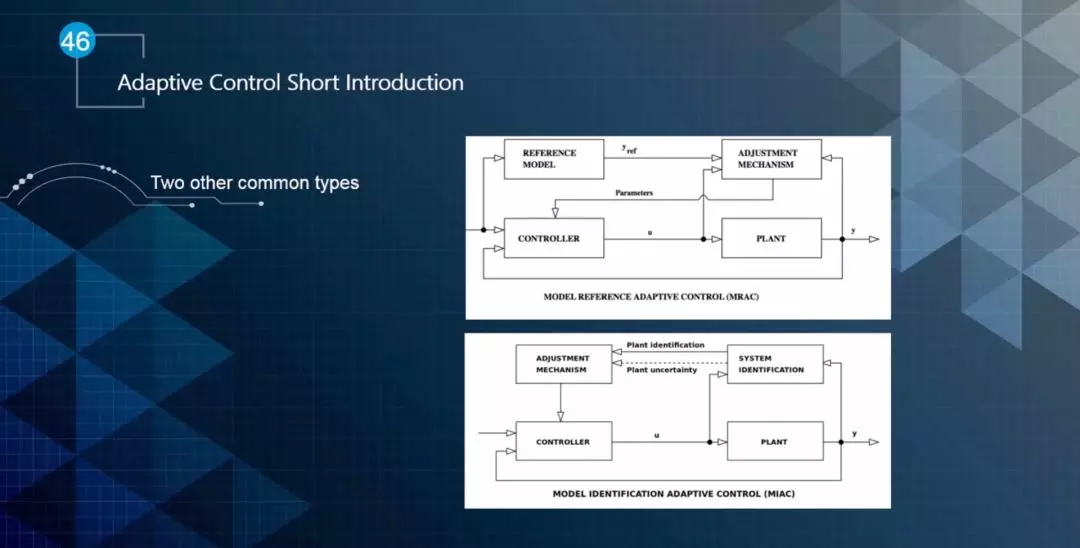
实际上，自适应控制更多的作为其他控制器的一种补充使用，图12展示了两种常用的模式。
▲图12 自适应控制的两种使用模式
关于自适应控制的更多详细介绍，可以参考图13列出的参考资料。
▲图13 自适应控制的相关参考资料
鲁棒性控制（Robust Control）
鲁棒性用来解决如何确定模型的正确性问题。它主要是用来处理模型的非确定性，是一种在已知模型错误边界的情况下，设计一个性能不错而且稳定的控制器的方法。最简单的鲁棒性控制器是LQR/LTR控制器，也是一个二次线性调节器，如图14所示。
▲图14 LQR/LTR控制器
离散化
首先，我们讨论为什么要做离散化。离散化实际上是在尽可能的保存连续空间信息的情况下，把连续空间的问题转换为离散空间的描述，使得计算机能够更好地处理。需要注意的是离散化跟Digital Stability是相关的，如果采样不够好，会丢失很多信息使得系统不稳定。
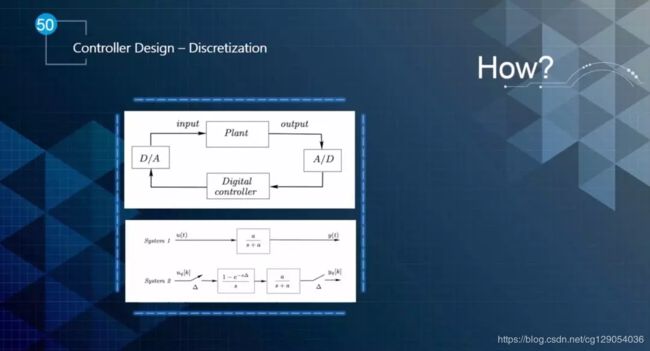
其此，如何进行离散化呢？离散化有很多的方法，各种方法都有各自的优缺点。但是总的来说都是把数字信号转换为模拟输入/输出信号，如图15所示。同样，也会把Analog输出进行离散化，然后输入到数字信号控制器中。
▲图15 控制器设计—离散化
图16是进行离散化的一个简单例子，左边是时域里的函数performance的表达方式，右边是进行离散化的一些常用表达形式。最后一列是收敛的速率，表示在一定工况下，数字控制器在给定的时间下是可以保证收敛的。
▲图16 控制器设计—离散化例子
图17给出了离散化时的一下简单转换公式对应关系。
▲图17控制器设计—离散化时转换公式对应关系
更多关于离散化的详细介绍可以参考图18列出的一些参考资料。
▲图18 离散化相关参考文献资料
2.控制器设计的其它方面
控制器设计，除了上面提到的比较重要的几个控制方法之外，还有其它次要的因素需要考虑，这些因素更多的是影响控制器的性能，包括Deadzone、饱和和抗饱和等。
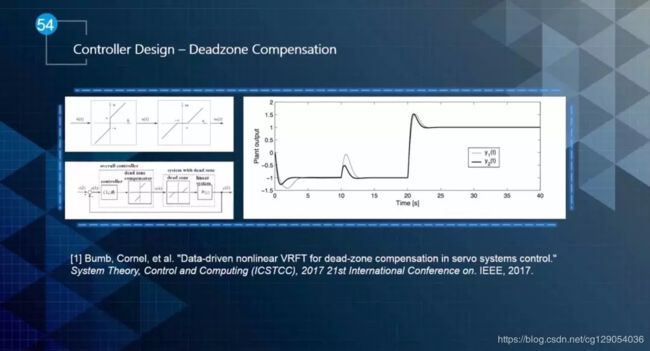
Deadzone主要是执行器的一些特性引起的，例如汽车的油门，可能给油0%～15%的区间都不会使汽车前行，这个时候反应在图上就是一条平行的线段，我们称之为Deadzone。在控制器设计的时候需要对这部分进行补偿设计，如图19所示。
▲图19 控制器设计—Deadzon补偿
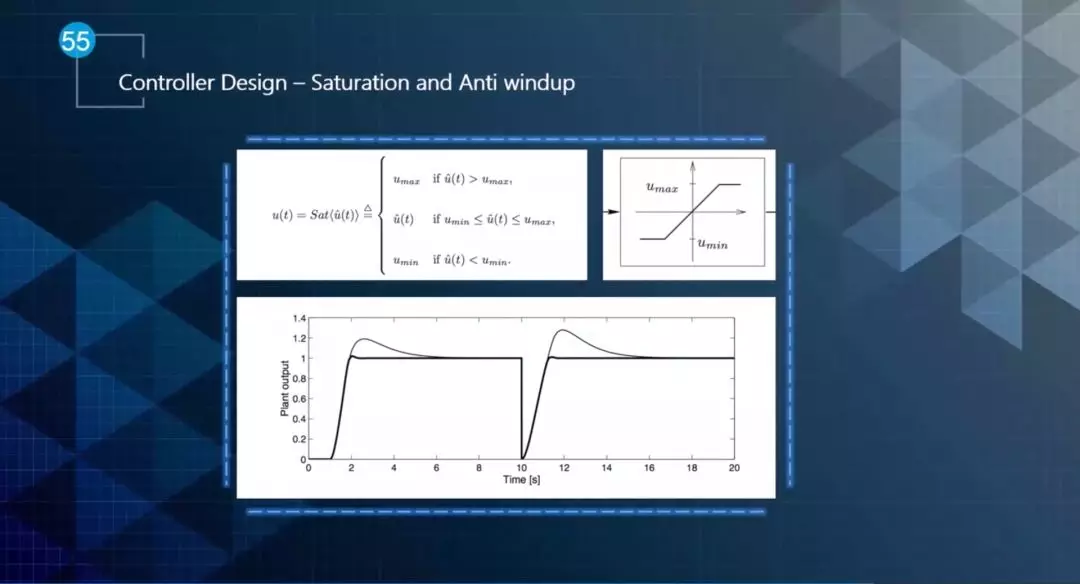
饱和和抗饱和处理也是出于对执行器的特性的考虑，通常一个执行器是有上限和下限的。如图20所示，把输出值做一个限制，使得输出在执行器的上下限范围内。如果不进行饱和处理，在输出100%的情况下突然转换状态，收敛到最终值可能需要很长的时间。
▲图20 饱和和抗饱和处理
关于Deadzone补偿和饱和、抗饱和的更多相关资料，可参考图21列出的参考文献。
▲图21 Deadzone补偿、饱和和抗饱和的相关参考文献
3.控制器的发展趋势
这部分更多的是讨论，目前还没有完整的理论或者应用案例。未来控制器可能从以下几个方面发展，如图22所示，包括数据驱动的控制、结合轨迹生成的控制、结合预测的控制、基于模型的增强学习控制方法。
▲图21 控制器的未来发展方向
4.工程应用案例
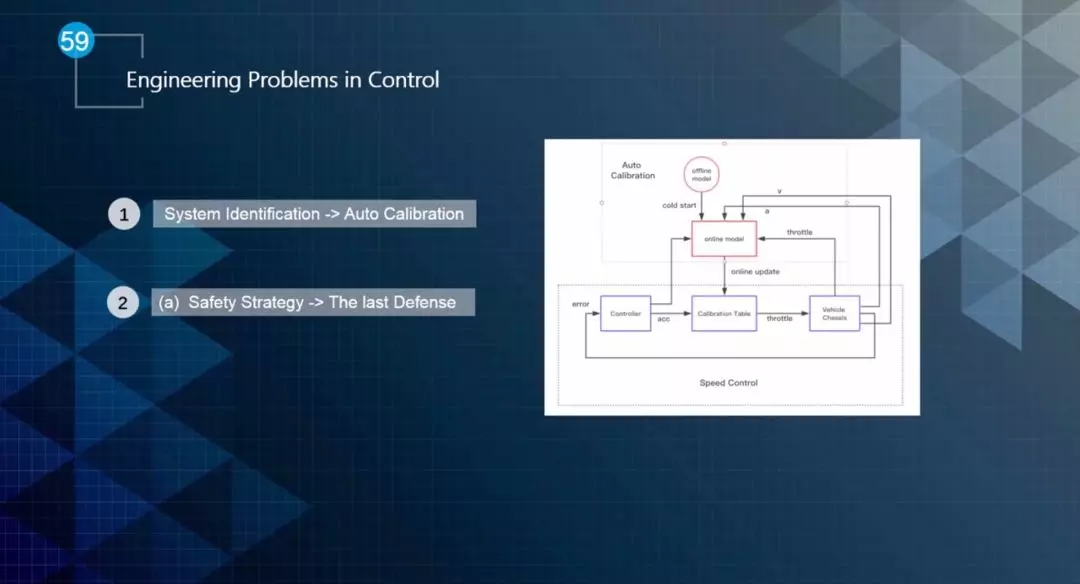
目前，在Apollo中，控制的工程应用主要有两个方面，一个是系统识别，使用的是自动标定方法。另一个是安全策略，如图23所示。
▲图23 工程应用案例
在自动驾驶系统中，有很多的部件参数是不确定，供应商也不会提供，但是在控制或者其它模块可能需要对这些部件进行建模，首先就得识别部件的参数，通常采用的是自动标定的方法。
安全策略的考虑主要是基于控制是否与底层交流的最后一个模块，所以有很多的安全策略需在控制层面完成。安全信息可分为两个部分：上游信息（Planner发出）+下层反馈信息。如果上游Planning信息丢失、延时、未更新，控制系统需要做出诸如Emergency Stop、缓行之类的决策。类似的，由于接触不稳或者其它因素，导致控制指令没有执行，控制器也需要做一些安全策略的考虑。