巨大数运算

巨大数的运算：

由于实现了包含整数和小数的运算，小数的除法运算比较繁琐且有比较高的难度，所以在有限的时间内只完成了加、减、乘这三则运算。后期如需增加除法运算，只需完成相关函数编写，此代码无需改动。

由于当前计算机对于数据的处理是存在一定限度的，c语言提供了许多整数类型，一般情况下使用int类型，但int类型的范围在-217483648~2147483647，当数据超出该范围时就需要使用另外的方法对这些数据进行处理，虽然float类型和double类型

也可以使用，但是float的有效位数只有7位，double类型的有效位数也只有15位，处理小数时精确度太低，小数位数越多，丢失的信息也就越大。因此需要提供一种对位数超出表示范围的数据的处理工具—也就是这个巨大数的处理工具。

#include 
#include 
#include 

typedef unsigned char boolean;

#define	TRUE			0
#define	FALSE			1
#define POSITIVE_SIGN           0
#define NEGATIVE_SIGN           1
#define MAX_BIT                 9999
#define MIN_BIT		        0

1.存储 

要处理巨大数的存储和表示；首先想到的就是字符串，但是使用字符串的弊端是存在很多次的类型转换，因此，在这里采用万进制的存储方式。万进制的原理同二进制十进制一样，万进制就是逢万进一。

例如：

2635938756 可表示为：26+3593+8756；

因为在乘法运算中1000010000的值在int的范围之内，而100000100000则超出了int可表示的范围。使用万进制，每次将存储四个字节，数组中的每个元素取值为0~9999，和使用字符串的效率相同。在这里，巨大数是从.txt文件中读取的，所以后续会采用文件操作。

typedef struct HUGENUMBER {
	boolean hugeSign;  //符号位 
	int *hugeArray;    //存放巨大数的数组 
	int hugeCount;     //巨大数数组元素个数    
	int point;         //小数点
}HUGENUMBER;

 2.初始化巨大数

假设文件中存放的数都是合法的。先判断第一个字符是否为符号（可能是‘-’、‘+’或无符号），并记录下来，巨大数的实际长度应该从第一个数字开始。因为包含小数部分，所以这里将整数与小数分开处理，只用记录小数点位置。巨大数位数hugeCount = decimalLenth + integerLenth，根据得到的位数就去申请存放巨大数的数组空间，因为存储方式是4位一组，则数组的长度 = (位数 + 3) / 4。存放时巨大数最高位的数据需单独处理，因为最高位的数字不一定是4个，例如26 3593 8756，先存放高位的26，存放最高位数字方法如下：（integerLenthDigit 是一个辅助变量）

定义一个只读数组const char *format[4] = {"%4d", "%1d", "%2d", "%3d"};将hugeCount % 4作为数组下标取出相应字符串，做为fscanf函数的格式符。

    fscanf(fp, format[integerLenthDigit % 4], &hugeNumber->hugeArray[hugeNumber->hugeCount - 1]);

剩下的数字按每4位依次读取并按顺序存放，小数部分则直接按每4位读取并依次存放，数组最后一个元素中存放的数字也不一定是4个，但根据高高低低原则，个数不够的在后面补0，并不影响数值的结果和计算。

void initHugeNumber(HUGENUMBER *hugeNumber, FILE *fp) {
	const char *format[4] = {"%4d", "%1d", "%2d", "%3d"};
	int firstIndex;                 //初始下标；
	int fileLenth;			//总长；
	char firstSign;                 //第一个符号；
	int integerLenth;		//整数位数；
	int decimalLenth;		//小数长度；
	int integerLenthDigit;    	//整数位数(辅助变量)；
	char ch;
	int i;
	int j;
	int p;
	int q;
	int index;

	fseek(fp, 0, SEEK_SET);
	fread(&firstSign, sizeof(char), 1, fp);
	firstIndex = (firstSign >= '0' && firstSign <= '9') ? 0 : 1;

	fseek(fp, 0, SEEK_END);
	fileLenth = ftell(fp);
	q = fileLenth;
	fileLenth += (firstSign >= '0' && firstSign <= '9') ? 0 : -1;
	integerLenth = fileLenth;

	fseek(fp, 0, SEEK_SET);
	for(i = 0; i < q; i++) {
		ch = fgetc(fp);
		if(ch == '.') {
			integerLenth = i;
			fileLenth--;
		}
	}

	if(firstSign < '0' || firstSign > '9') {
		integerLenthDigit = integerLenth - 1;
	} else {
		integerLenthDigit = integerLenth;
	}

	decimalLenth = fileLenth - integerLenthDigit;
	index = decimalLenth % 4;
	decimalLenth = (decimalLenth + 3) / 4;
	hugeNumber->point = -decimalLenth;
	integerLenth = (integerLenthDigit + 3) / 4;

	fseek(fp, firstIndex, SEEK_SET);
	hugeNumber->hugeSign = (firstSign == '-') ? NEGATIVE_SIGN : POSITIVE_SIGN;
	hugeNumber->hugeCount = decimalLenth + integerLenth;		//(fileLenth + 3) / 4;
	hugeNumber->hugeArray = (int *) calloc(sizeof(int), hugeNumber->hugeCount);

	fscanf(fp, format[integerLenthDigit % 4], &hugeNumber->hugeArray[hugeNumber->hugeCount - 1]);
	j = hugeNumber->hugeCount - 1;

	for(i = 0; i < integerLenth - 1; i++) {
        fscanf(fp, "%4d", &hugeNumber->hugeArray[--j]);
    }

    fgetc(fp);
    for(i = decimalLenth - 1; i >= 0; i--) {
        fscanf(fp, "%04d", &hugeNumber->hugeArray[i]);
    }

    while(index) {
        hugeNumber->hugeArray[0] *= 10;
        index = (index + 1) % 4;
    }
}

3.巨大数的对齐

因为小数的参与，巨大数的运算就不单单是从低位向高位进行加减运算了。首先我们需要将两个巨大数按小数点位置对齐，整数长度取整数位数高的巨大数整数长度，小数长度取小数位数高的巨大数小数长度，空余的位置补 0 (注意：calloc自动初始化该内存空间为零)，不影响数据的值。

void fillHugeNumber(HUGENUMBER *hugeNumber1, HUGENUMBER *hugeNumber2, HUGENUMBER *tmpHugeNumber1, HUGENUMBER *tmpHugeNumber2) {
	int i;
	int point1;
	int point2;
	int point;
	int initLenth1;
	int initLenth2;
	int initLenth;
	int lenth;

	point1 = abs(hugeNumber1->point);
	point2 = abs(hugeNumber2->point);
	initLenth1 = hugeNumber1->hugeCount - point1;
	initLenth2 = hugeNumber2->hugeCount - point2;
	point1 > point2 ? (point = point1) : (point = point2);
	initLenth1 > initLenth2 ? (initLenth = initLenth1) : (initLenth = initLenth2);
	lenth = initLenth + point;
    tmpHugeNumber1->hugeArray = (int *) calloc(sizeof(int), lenth);
    tmpHugeNumber2->hugeArray = (int *) calloc(sizeof(int), lenth);

    for(i = 0; i < point1; i++) {
    	tmpHugeNumber1->hugeArray[point - i - 1] = hugeNumber1->hugeArray[point1 - i - 1];
    }

    for(i = 0; i < initLenth1; i++) {
    	tmpHugeNumber1->hugeArray[point + i] = hugeNumber1->hugeArray[point1 + i];
    }

    for(i = 0; i < point2; i++) {
    	tmpHugeNumber2->hugeArray[point - i - 1] = hugeNumber2->hugeArray[point2 - i - 1];
    }

    for(i = 0; i < initLenth2; i++) {
    	tmpHugeNumber2->hugeArray[point + i] = hugeNumber2->hugeArray[point2 + i];
    }

 	free(hugeNumber1->hugeArray);
    free(hugeNumber2->hugeArray);

    hugeNumber1->hugeArray = tmpHugeNumber1->hugeArray;
    hugeNumber2->hugeArray = tmpHugeNumber2->hugeArray;
    hugeNumber1->hugeCount = lenth;
    hugeNumber2->hugeCount = lenth;
}

4.巨大数的加法

处理巨大数时，为了避免对负数操作过程中的复杂运算（借位），在此引进微易码补码（此方法目前并没有数学理论证明，但经大量实验证实其方法计算结果准确无误！），与反码的原理相似。微易码补码是将负数除符号位外按位取反，也就是用9减去每一位。

如：-123 4567对应的补码为9876 5432；

符号位的确定。将负号记为 1 ，正号记为 0 。经过多次的推导又有结论：计算结果的符号位的确定是用两个数的符号位和进位按位异或。

如：12+345 符号位就是0^0^0 = 0；                         10-22   符号位就是0^1^0 = 1；

相加时需要考虑进位问题，无进位时计算结果无误。但有进位时，微易码补码会出现错误，例子如下：

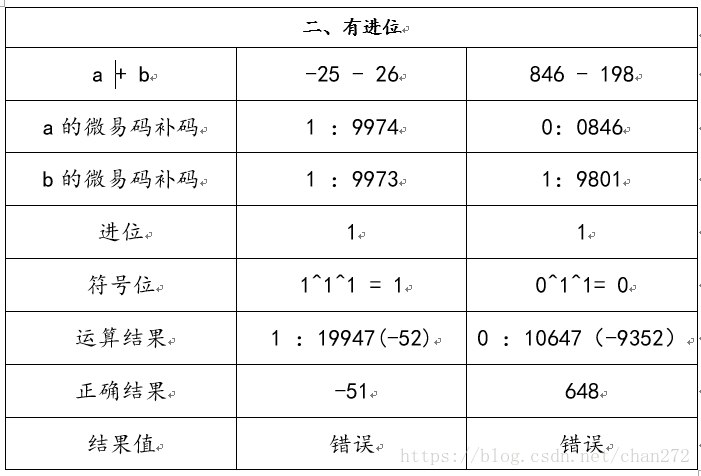
由上表可得，在有进位时，微易码补码在一定情况下出现错误，但是如果将进位的结果加到最后运算的值上，即对9947再加上进位就是9948，转换过后就是-51，而且这个规律运用到无进位的计算中也是正确的。但是在此又需要考虑另一种情况，会出现过饱和状态。如：在两个数最高位相加时 9990 + 1000 =1 0990，进位是 1 。所以在这种情况下，对于结果在申请空间时就得多申请一个空间，作为数据前的辅助位，正数为0000，负数为9999。

HUGENUMBER addHugeNumber(HUGENUMBER *hugeNumber1, HUGENUMBER *hugeNumber2) {
	HUGENUMBER result = {0};
	int tmpLenth;
	int tmp;
	int carry = 0;
	int i;
	int point1;
	int point2;
	int biteResult;

    result.hugeCount = hugeNumber1->hugeCount + 1;
	tmpLenth = result.hugeCount;
	result.hugeArray = (int *) calloc(sizeof(int), result.hugeCount);
	
	getCompliment(hugeNumber1);
	getCompliment(hugeNumber2);	

	for(i = 0; i < result.hugeCount - 1; i++) {
		biteResult = hugeNumber1->hugeArray[i] + hugeNumber2->hugeArray[i];
		result.hugeArray[i] = (biteResult + carry) % 10000;
		carry = (biteResult + carry) / 10000;
	}

	result.hugeSign = hugeNumber1->hugeSign ^ hugeNumber2->hugeSign ^ carry;
	if(hugeNumber1->hugeSign == NEGATIVE_SIGN && hugeNumber2->hugeSign == NEGATIVE_SIGN) {
		result.hugeArray[0] += 1;
	} 			
	//当两个负数相加时，需要在结果最后一位加1！
	
	if(result.hugeArray[result.hugeCount - 1] == 0) {
		result.hugeCount = result.hugeCount	- 1;
	}

	getCompliment(&result);

	point1 = abs(hugeNumber1->point);
    point2 = abs(hugeNumber2->point);
    result.point = -(point1 > point2 ? point1 : point2); 

	return result;
}

5.巨大数减法

如上一步加法所述，遇到减法或负数时，将其转化为微易码补码的形式进行加法运算，只需要增加一个补码转换函数。

void getCompliment(HUGENUMBER *hugeNumber) {
	int i;

	if(hugeNumber->hugeSign == NEGATIVE_SIGN) {
		for (i = 0; i < hugeNumber->hugeCount; i++) {
        hugeNumber->hugeArray[i] = 9999 - hugeNumber->hugeArray[i];
    	}
	} else {

		return;
	}
}

6.巨大数乘法

乘法的运算与十进制相同，按位相乘。上述过程中进行了小数点对齐工作，乘法在此变得更为容易，只需计算小数点位置和存储结果的数组长度，长度应为两个乘数的长度之和。结果的符号位：两个乘数符号相同则为正，不同则为负。结果则是将每次的乘积相加。

HUGENUMBER multiplyHugeNumber(HUGENUMBER hugeNumber1, HUGENUMBER hugeNumber2) {
	int i;
	int j;
	int carry;
	int resultIndex;
	int point1;
	int point2;
	int eachResult;
	HUGENUMBER mulResult = {0};

	mulResult.hugeCount = hugeNumber1.hugeCount + hugeNumber2.hugeCount;
	mulResult.hugeArray = (int *) calloc(sizeof(int), mulResult.hugeCount);

	mulResult.hugeSign = (hugeNumber1.hugeSign == hugeNumber2.hugeSign) ? 0 : 1;
	for(i = 0; i < hugeNumber1.hugeCount; i++) {
		carry = 0;
		resultIndex = i;
		for(j = 0; j < hugeNumber2.hugeCount; j++) {
			eachResult = hugeNumber1.hugeArray[i] * hugeNumber2.hugeArray[j] + carry;
			carry = (mulResult.hugeArray[resultIndex] + eachResult) / 10000;
			mulResult.hugeArray[resultIndex] = (mulResult.hugeArray[resultIndex] + eachResult) % 10000;
			resultIndex++;
		}
		mulResult.hugeArray[resultIndex] = carry;
	}
	point1 = abs(hugeNumber1.point);
	point2 = abs(hugeNumber2.point);
	mulResult.point = -(point1 + point2);

	return mulResult;
}

7.巨大数的输出

将符号单独输出，再依次输出数组元素，遇到小数点时输出小数点。

void showHugeNumber(HUGENUMBER hugeNumber) {
	int i;
	int point = abs(hugeNumber.point);

	printf("%c", (hugeNumber.hugeSign == 1) ? '-' : ' ');
	printf("%d", hugeNumber.hugeArray[hugeNumber.hugeCount - 1]);
	for(i = hugeNumber.hugeCount - 2; i >= 0; i--) {
		if(i == point - 1) {
			printf(".");
		}
		printf("%04d", hugeNumber.hugeArray[i]);
	}
	printf("\n");
}

8.文件操作及主函数

主函数可根据自己意愿更改。

boolean readFile(HUGENUMBER *hugeNumber, const char *fileName) {
	FILE *fp;

	fp = fopen(fileName, "r");
	if(NULL == fp) {
		printf("该文件不存在！");
		return FALSE;
	} 

	initHugeNumber(hugeNumber, fp);

	return TRUE;
}


int main() {
	const char *fileName1 = "./data1.txt";
	const char *fileName2 = "./data2.txt";

	HUGENUMBER hugeNumber1 = {0};
	HUGENUMBER hugeNumber2 = {0};
	HUGENUMBER result1 = {0};
	HUGENUMBER result2 = {0};
	HUGENUMBER tmpHugeNumber1 = {0};
	HUGENUMBER tmpHugeNumber2 = {0};

	readFile(&hugeNumber1, fileName1);
	readFile(&hugeNumber2, fileName2);
	showHugeNumber(hugeNumber1);
	showHugeNumber(hugeNumber2);

	result1 = multiplyHugeNumber(hugeNumber1,  hugeNumber2);
	showHugeNumber(result1);

	fillHugeNumber(&hugeNumber1, &hugeNumber2, &tmpHugeNumber1, &tmpHugeNumber2);
	//showHugeNumber(hugeNumber1);
	//showHugeNumber(hugeNumber2);

	result2 = addHugeNumber(&hugeNumber1, &hugeNumber2);

	showHugeNumber(result2);

	free(hugeNumber1.hugeArray);
	free(hugeNumber2.hugeArray);
	free(result1.hugeArray);
	free(result2.hugeArray);

	return 0;
}