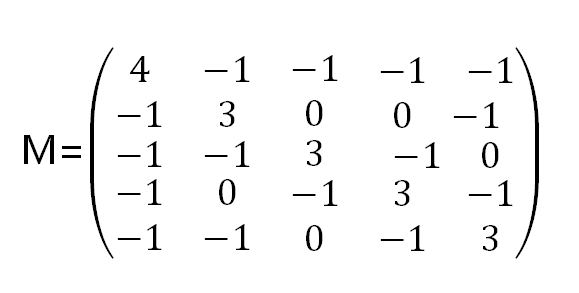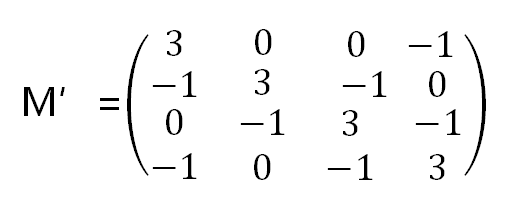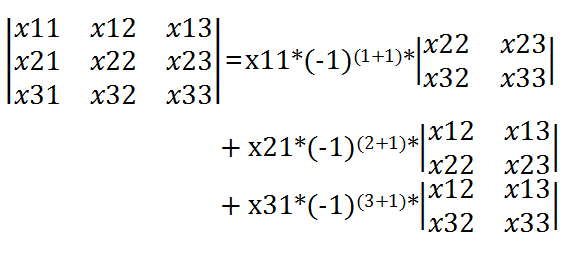无向连通图的生成树个数
我们知道，每个无向连通图都会有自己的生成树。但是大家更熟悉的，是无向图的最小生成树（MST）算法。本文旨在讨论计算无向连通图的生成树个数的时间复杂度为O(n3)的方法。另外一种时间效率高的递推式方法的讲解在文末附有链接。
我们可以利用矩阵在O(n3)的时间内求出无向连通图的生成树个数。对于一个无向连通图，我们可以根据以下规则列出一个矩阵M：
- 主对角线上的值M(i,i)为i节点的度。
- a[i,j]的值为点i到点j的平行边的条数的相反数。显然，如果i,j不连通，M(i,j)=0。
通过这样的规则，一个矩阵就在O(n2)的时间内建立起来。
以图1为例。
这样，我们就得到了矩阵M:
参考代码（init）：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
begin
fillchar(ma,sizeof(ma),
0
);
readln(n,m);
for
i:=
1
to
n
do
for
j:=
1
to
n
do
begin
read(x);
if
x=
1
then
begin
ma[i,i]:=ma[i,i]+
1
;
ma[i,j]:=-
1
;
end
;
end
;
end
.
|
恩，有了这个矩阵有什么用呢？
【定理】删除矩阵中任意一个节点的信息，求出剩下的(n-1)*(n-1)矩阵的行列式的值，此值即为这个无向连通图的生成树个数。
定理的证明在这里不再赘述（其实我也不会，知道怎么证明又有什么用呢 可以用数学归纳法证明），如果想知道详细的证明过程，可以参阅文末所附的参考文献，或者在网上查阅。
经过删除操作，我们得到如下的矩阵M’：
可是，行列式的值怎么求呢？
我们知道行列式值的手工求法是经过将行列式降阶，通过如下的定理求得：
【定理】三阶行列式D=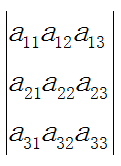 
的值等于它任意一行（列）的所有元素与它们对应的代数余子式乘积之和。
即：
用等式表示为：
当阶数很高，这种方法由于要递归、压栈，不但占用大量内存，而且代码复杂度很高（现在我还没有打出来过 *.*||）。在这里，我们用高斯消元的思想将行列式转化成一个下三角行列式，运用以下性质即可求出行列式的值。
【性质】三角形行列式的值等于主对角线上元素的乘积。
这样，只要我们将行列式进行消元，然后求得主对角线上元素的乘积即可。
参考代码（make）：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
begin
ans:=
1
;
for
k:=
1
to
n
do
begin
ans:=ans*a[k,k];
//记录对角线乘积
for
i:=k+
1
to
n
do
if
a[i,k]<>
0
then
begin
zoom:=-a[k,k]/a[i,k];
ans:=ans/zoom;
//ans也要zoom一下
for
j:=k
to
n
do
a[i,j]:=a[k,j]+a[i,j]*zoom;
//消元
end
;
end
;
writeln
(round(ans));
end
;
|
下面是一道例题。
【问题描述】 小夜家教很严……恩，家教很严厉。但俗话说得好“有些鸟是关不住的”。小夜家住一个很大很大
的湖泊中央的小岛上，湖泊中有还有n个小岛，小岛间有桥相连。任意两个小岛之间都有至少一条路径可
以到达。小夜很久没有出去玩了，她想到岸上去玩……但是去玩之前她要跟自己的爷爷奶奶叔叔伯伯阿
姨婶婶大哥大姐小弟小妹打声招呼，所以她要跑遍湖中所有的岛至少一次（当然还有自己家），但是小
夜有个很邪恶的爸爸，夜爸爸不准小夜出去玩。夜爸爸有足够的人手可以控制住连接岛屿的桥，在从线
人那打听到小夜的情况后，夜爸爸决定在每一个时刻都增派一票人控制住某一座当前还未被他控制的桥，
只要小夜路过这些桥就…… 小夜在路上好几次都差点被逮到，她发现这是个问题，于是打开手机向你求助。因为被夜爸爸控制
的桥会越来越多，她认为走的桥越少越好，所以她想知道当前时刻一共有多少种方案能够让选择n座桥
并使得任意两个岛屿只有一条路径连通。 【输入格式】 输入文件第一行两个整数n和m，表示湖泊中除了小夜家以外的岛屿数目和夜爸爸会陆续派m票人控
制桥。 接下来n+1行，每行n+1个整数，其中第i行第j个整数 Aij表示第i号岛屿和第j号岛屿之间是否直
接有桥相连（0表示不连通，1表示连通）。 再接下来m行，每行两个整数a，b。表示当前时刻他已经控制住第a号岛屿和第b号岛屿直接相连的
桥。（注：开始时刻夜爸爸没控制一座桥。） 【输出格式】 输出文件共有m+1行，每行一个整数。表示当前时刻的总方案数。 【输入样例】
5
2
0
1
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
0
1
4
1
1
3 【输出样例】
1296
864
540 【数据范围】 对于40%的数据
013 对于100%的数据
026 ,
031 输出数据保证在extended范围内。
首先注意，解不是n!。原因是路线不一定是链状的，而可能是树状的。这样，问题就转化成求无向连通图的生成树个数的问题了。
参考代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
program
escape;
var
a,ta:
array
[
1..30
,
1..30
]
of
extended
;
n,m,x,y,i:
integer
;
ans:
extended
;
procedure
init;
var
i,j:
integer
;
begin
readln(n,m);
for
i:=
1
to
n+
1
do
for
j:=
1
to
n+
1
do
begin
read(x);
if
x=
1
then
begin
a[i,i]:=a[i,i]+
1
;
a[i,j]:=-
1
;
end
;
end
;
ta:=a;
end
;
procedure
make;
var
i,j,k:
integer
;
zoom:
extended
;
begin
ans:=
1
;
for
k:=
1
to
n
do
begin
ans:=ans*a[k,k];
for
i:=k+
1
to
n
do
if
a[i,k]<>
0
then
begin
zoom:=-a[k,k]/a[i,k];
ans:=ans/zoom;
for
j:=k
to
n
do
a[i,j]:=a[k,j]+a[i,j]*zoom;
end
;
end
;
writeln
(round(ans));
end
;
begin
init;
make;
for
i:=
1
to
m
do
begin
readln(x,y);
ta[x,x]:=ta[x,x]-
1
;
ta[y,y]:=ta[y,y]-
1
;
ta[x,y]:=
0
;
ta[y,x]:=
0
;
a:=ta;
//记录原图
make;
end
;
end
.
|
参考链接（均有递推式法