MPC(3)常用车辆模型
上一篇中介绍了,模型预测控制的理论方面基础,无人驾驶车辆采用MPC控制方法来进行相关控制的时候,就考虑结合车辆的运动学以及动力学的相关约束。而且,如果在路径规划阶段(Local Planner)就考虑到车辆运动学和动力学约束,则车辆运动跟踪性能会更好。这篇文章就主要介绍的就是,前轮驱动小轿车目前常用的几种车辆运动学以及动力学模型。
阿克曼模型
车辆低速行驶时,轮胎不会产生侧滑,同时,车辆转向时,左前轮和右前轮偏转的角度是不同的,如下图所示(画图很麻烦,所以图片很多都是网上找的)
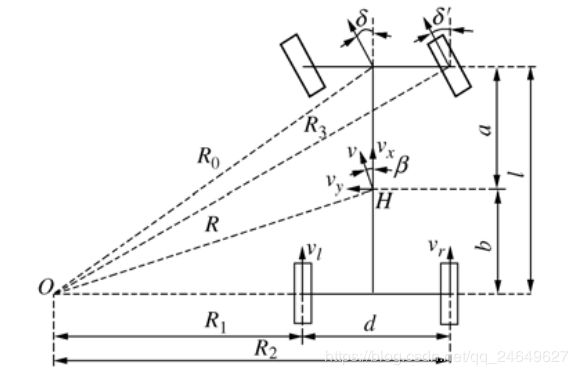
由于两个前轮的转向角度不同,造成了,两个后轮旋转半径也不相同,于是,做出了相应的简化,以车辆后轴中心点为旋转参考点,对车辆左前轮角度和右前轮角度取均值:
δ = δ l + δ r (1) \delta = \delta_l + \delta_r \tag{1} δ=δl+δr(1)
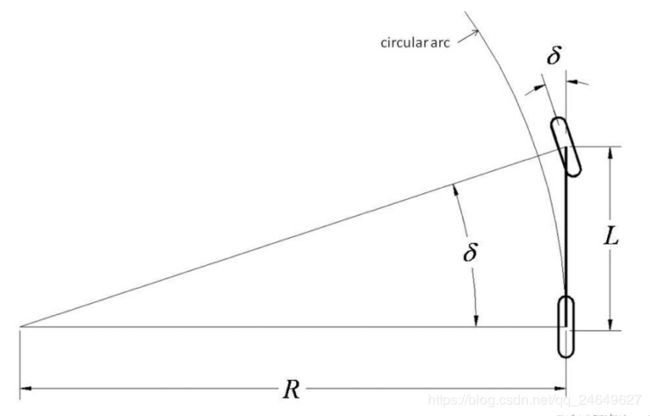
式中, δ \delta δ为简化后车辆前轮转向角, δ l \delta_l δl和 δ r \delta_r δr分别为对应的车辆左侧前轮角度和右侧前轮转向角度。简化后的模型,称为自行车模型,自行车模型最大的好处就是把前轮转角与车辆后轴质心旋转的半径联系了起来。
t a n δ = L R (2) tan \space \delta = \frac{L}{R} \tag{2} tan δ=RL(2)
其中, δ \delta δ 为车辆前轮转角
L L L 为车辆前后轴之间的距离(Wheel Base)
R R R 为车辆在给定的前轮转角 δ \delta δ情况下,所遵循的圆轨迹的半径。
车辆运动学模型
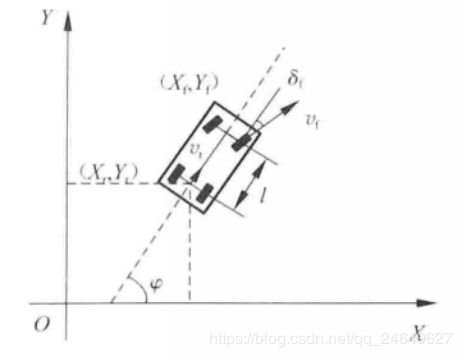
如下图所示,车辆转向模型:
在惯性坐标系XOY下, ( X f , Y f ) (X_f,Y_f) (Xf,Yf)和 ( X r , Y r ) (X_r,Y_r) (Xr,Yr)分别代表车辆后轴中心和前轴中心的坐标, φ \varphi φ表示车辆的航向角, δ f \delta_f δf表示前轮偏角, v r v_r vr表示车辆后轴中心沿车辆轴线方向的速度, δ f \delta_f δf表示车辆前轴中心沿着前轮偏角方向的速度, l l l表示车辆前后轴之间的距离。
在车辆后轴中心 ( X r , Y r ) (X_r,Y_r) (Xr,Yr)处,有
v r = X ˙ r ∗ c o s ( φ ) + Y ˙ r ∗ s i n ( φ ) (3) v_r = \dot{X}_{r}*cos (\varphi) + \dot{Y}_{r}*sin(\varphi) \tag{3} vr=X˙r∗cos(φ)+Y˙r∗sin(φ)(3)
前、后轴的运动学约束(车辆无横向侧滑):
{ X ˙ f ∗ s i n ( φ + δ f ) − Y ˙ f ∗ c o s ( φ + δ f ) = 0 X ˙ r ∗ s i n ( φ ) − Y ˙ r ∗ c o s ( φ ) = 0 (4) \begin{cases} \dot{X}_{f}*sin(\varphi + \delta_f) - \dot{Y}_{f}*cos(\varphi + \delta_f) = 0 \\ \dot{X}_{r}*sin(\varphi) - \dot{Y}_{r}*cos(\varphi) = 0 \end{cases} \tag{4} {X˙f∗sin(φ+δf)−Y˙f∗cos(φ+δf)=0X˙r∗sin(φ)−Y˙r∗cos(φ)=0(4)
根据式(3)、式(4)可以得出:
{ X ˙ r = v r ∗ c o s ( φ ) Y ˙ r = v r ∗ s i n ( φ ) (5) \begin{cases} \dot{X}_{r} = v_r*cos(\varphi) \\ \dot{Y}_{r} = v_r*sin(\varphi) \\ \end{cases} \tag{5} {X˙r=vr∗cos(φ)Y˙r=vr∗sin(φ)(5)
根据前后轮的位置关系有:
{ X f = X r + l ∗ c o s φ Y f = Y r + l ∗ s i n φ (6) \begin{cases} X_f = X_r + l*cos\varphi \\ Y_f = Y_r + l*sin\varphi \\ \end{cases} \tag{6} {Xf=Xr+l∗cosφYf=Yr+l∗sinφ(6)
将(5)、(6)带入(4)可以得出横摆角 ω \omega ω速度为:
φ ˙ = ω = v r l ∗ t a n ( δ f ) (7) \dot\varphi=\omega = \frac{v_r}{l}*tan(\delta_f) \tag{7} φ˙=ω=lvr∗tan(δf)(7)
由横摆角 ω \omega ω和车速 v r v_r vr可以计算出车辆在不同的前轮转向角的条件下,对应的不同转向半径(可以看出与阿克曼模型的转弯半径计算方式相同):
{ R = v r ∗ ω δ f = a r c t a n ( l R ) (8) \begin{cases} R = v_r*\omega \\ \delta_f = arctan(\frac{l}{R}) \end{cases} \tag{8} {R=vr∗ωδf=arctan(Rl)(8)
由式(5),(7)可以得出车辆运动学模型
[ X ˙ r Y ˙ r φ ˙ ] = [ c o s φ s i n φ t a n ( δ f ) / l ] ∗ v r (9) \begin{bmatrix} \dot{X}_{r} \\ \dot{Y}_{r} \\ \dot{\varphi} \end{bmatrix} = \begin{bmatrix} cos \varphi \\ sin \varphi \\ tan(\delta_f)/l \end{bmatrix} *v_r \tag{9} ⎣⎡X˙rY˙rφ˙⎦⎤=⎣⎡cosφsinφtan(δf)/l⎦⎤∗vr(9)
车辆的可控制量为 v r v_r vr和 δ f \delta_f δf,而在实际使用中,最好的方式是希望以 [ v r , ω ] [v_r,\omega] [vr,ω]作为控制量,将式(7)带入式(9)中,可以将车辆运动学模型可以被转换为以下形式:
[ X ˙ r Y ˙ r φ ˙ ] = [ c o s φ s i n φ 0 ] ∗ v r + [ 0 0 1 ] ∗ ω (10) \begin{bmatrix} \dot{X}_{r} \\ \dot{Y}_{r} \\ \dot{\varphi} \end{bmatrix} = \begin{bmatrix} cos \varphi \\ sin \varphi \\ 0 \end{bmatrix} *v_r + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} * \omega \tag{10} ⎣⎡X˙rY˙rφ˙⎦⎤=⎣⎡cosφsinφ0⎦⎤∗vr+⎣⎡001⎦⎤∗ω(10)
由车辆运动学模型可以看作是对阿克曼运动模型的延伸,通过运动学方程可以计算出控制时域内,可以计算出车身后轴中心点坐标 X X X, Y Y Y以及航向角 φ \varphi φ在预测时间内的变化量。
车辆动力学模型
在进行车辆动力学建模时,首先要进行以下理想化假设:
- 假设车辆在平坦路面上行驶,忽略车辆的垂向运行
- 忽略悬架系统运动造成的相关影响
- 只考虑纯侧偏轮胎特性,忽略轮胎力的纵横向耦合关系
- 忽略车辆前后以及左右向的载荷转移
- 忽略纵向横向的空气动力学
同样,设定车辆为前轮驱动,以车辆质心为原点 O O O,沿着车辆纵向轴线指向车头方向为 X X X轴正向,垂直于车辆,车身水平面内垂直于 X X X轴且指向车身左侧方向为 Y Y Y轴, Z Z Z轴垂直于 X Y XY XY面且垂直向上。具体如下图所示:
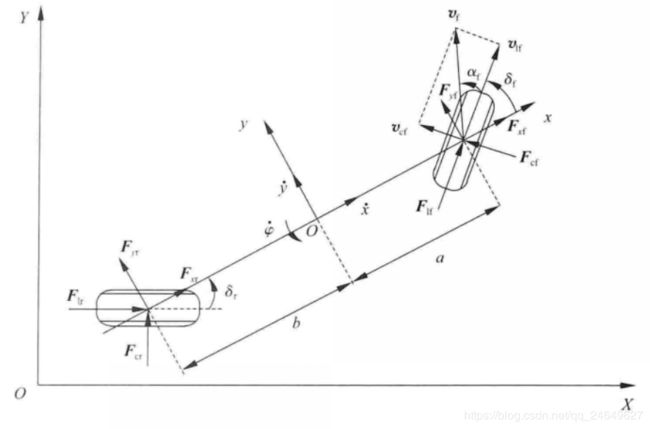
关于其中轮胎受力定义如下:
F l f , F l r F_lf,F_lr\space Flf,Flr —— 前、后轮胎受到的纵向力
F c f , F c r F_cf,F_cr Fcf,Fcr —— 前、后轮胎受到的侧向力
F x f , F x r F_xf,F_xr Fxf,Fxr —— 前、后轮胎受到的x方向的力
F y f , F y r F_yf,F_yr Fyf,Fyr —— 前、后轮胎收到的y方向的力
根据牛顿第二定律,分别可得沿 x x x轴, y y y轴和绕 z z z轴的受力平衡方程
在 X X X轴方向上:
m ∗ x ¨ = m ∗ y ˙ ∗ φ ˙ + 2 ∗ F x f + 2 ∗ F x r (11) m*\ddot{x} = m*\dot{y}*\dot{\varphi} + 2*F_{xf} + 2*F_{xr} \tag{11} m∗x¨=m∗y˙∗φ˙+2∗Fxf+2∗Fxr(11)
在 Y Y Y轴方向上:
m ∗ y ¨ = − m ∗ x ˙ ∗ φ ˙ + 2 ∗ F y f + 2 ∗ F y r (12) m*\ddot{y} = -m*\dot{x}*\dot{\varphi} + 2*F_{yf} + 2*F_{yr} \tag{12} m∗y¨=−m∗x˙∗φ˙+2∗Fyf+2∗Fyr(12)
绕 Z Z Z轴方向:
I z ∗ φ ¨ = 2 ∗ a ∗ F y f − 2 ∗ b ∗ F y r (13) I_{z}*\ddot{\varphi}= 2*a*F_{yf}-2*b*F_{yr} \tag{13} Iz∗φ¨=2∗a∗Fyf−2∗b∗Fyr(13)
式中, a a a和 b b b分别为质心到前、后轴的距离, m m m为车辆装备质量, I z I_z Iz为车辆绕 z z z轴的转动惯量。
轮胎在 x , y x,y x,y方向上受到的合力与纵向、侧向力的转换关系如下:
{ F x f = F l f ∗ c o s ( δ f ) − F c f ∗ s i n ( δ f ) F x r = F l r ∗ c o s ( δ r ) − F c r ∗ s i n ( δ r ) F y f = F l f ∗ s i n ( δ f ) + F c f ∗ c o s ( δ f ) F y r = F l r ∗ s i n ( δ r ) + F c r ∗ c o s ( δ r ) (14) \begin{cases} F_{xf} = F_{lf}*cos(\delta_f)-F_{cf}*sin(\delta_f) \\ F_{xr} = F_{lr}*cos(\delta_r)-F_{cr}*sin(\delta_r) \\ F_{yf} = F_{lf}*sin(\delta_f)+F_{cf}*cos(\delta_f) \\ F_{yr} = F_{lr}*sin(\delta_r)+F_{cr}*cos(\delta_r) \tag{14} \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧Fxf=Flf∗cos(δf)−Fcf∗sin(δf)Fxr=Flr∗cos(δr)−Fcr∗sin(δr)Fyf=Flf∗sin(δf)+Fcf∗cos(δf)Fyr=Flr∗sin(δr)+Fcr∗cos(δr)(14)
轮胎的纵向力、侧向力可以表示为轮胎的侧偏角、滑移率、路面摩擦系数和垂向载荷等参数的复杂函数:
{ F l = f l ( α , s , μ , F z ) F c = f c ( α , s , μ , F z ) (15) \begin{cases} F_l=f_l(\alpha,s,\mu,F_z) \\ F_c=f_c(\alpha,s,\mu,F_z) \end{cases} \tag{15} {Fl=fl(α,s,μ,Fz)Fc=fc(α,s,μ,Fz)(15)
式中, α \alpha α为轮胎侧偏角, s s s为滑移率, μ \mu μ为路面摩擦系数, F z F_z Fz为轮胎所受到的垂向载荷。
轮胎的侧偏角 α \alpha α可以由几何关系计算得到:
α = a r c t a n v c v l (16) \alpha= arctan \frac{v_c}{v_l} \tag{16} α=arctanvlvc(16)
式中, v c v_c vc与 v l v_l vl为轮胎在侧向、纵向的速度,可以用坐标系方向的速度 v x v_x vx和 v y v_y vy表示:
{ v l = v y ∗ s i n δ + v x ∗ c o s δ v c = v y ∗ c o s δ − v x ∗ s i n δ (17) \begin{cases} v_l=v_y*sin\delta+v_x*cos\delta \\ v_c=v_y*cos\delta-v_x*sin\delta \end{cases} \tag{17} {vl=vy∗sinδ+vx∗cosδvc=vy∗cosδ−vx∗sinδ(17)
式中, δ \delta δ为轮胎偏转角。
轮胎的速度获取通常比较麻烦,现在的车子四个轮子在旋转时会发出相应的脉冲信号,通过解析这些信号获取四个轮子的轮速是一种很方便且精确的方式,另外一种就是通过车辆速度计算得出,这种方法虽说没有上一种方式精确,但是使用范围广泛,具体公式如下:
v y f = y ˙ + a ∗ φ ˙ v y r = y ˙ − b ∗ φ ˙ v x f = x ˙ v x r = x ˙ (18) \begin{matrix} v_{yf}= \dot{y}+a*\dot{\varphi} \\ v_{yr}= \dot{y}-b*\dot{\varphi} \\ v_{xf} = \dot{x} \\ v_{xr} = \dot{x} \end{matrix} \tag{18} vyf=y˙+a∗φ˙vyr=y˙−b∗φ˙vxf=x˙vxr=x˙(18)
轮胎在地面上的滑移率 s s s的计算公式:
s = { r ∗ w t v − 1 if v > r ∗ w t , v = / 0 1 − v r ∗ w t if v < r ∗ w t , w t = / 0 (19) s= \begin{cases} \frac{r*w_t}{v}-1 & \text{if} \space v>r*w_t,v {=}\mathllap{/\,}0 \\ 1-\frac{v}{r*w_t} & \text{if} \space v
式中, r r r为车轮半径, w t w_t wt为车轮旋转角速度。
车辆前后轴所受的垂向载荷:
{ F z f = b ∗ m ∗ g 2 ∗ ( a + b ) F z r = a ∗ m ∗ g 2 ∗ ( a + b ) (20) \begin{cases} F_{zf}=\frac{b*m*g}{2*(a+b)} \\ F_{zr}=\frac{a*m*g}{2*(a+b)} \end{cases} \tag{20} {Fzf=2∗(a+b)b∗m∗gFzr=2∗(a+b)a∗m∗g(20)
最后,考虑车身坐标系以及惯性坐标系之间的关系有:
{ Y ˙ = x ˙ ∗ s i n φ + y ˙ ∗ c o s φ X ˙ = x ˙ ∗ c o s φ − y ˙ ∗ s i n φ (21) \begin{cases} \dot{Y}=\dot{x}*sin\varphi+\dot{y}*cos\varphi \\ \dot{X}=\dot{x}*cos\varphi-\dot{y}*sin\varphi \end{cases} \tag{21} {Y˙=x˙∗sinφ+y˙∗cosφX˙=x˙∗cosφ−y˙∗sinφ(21)
以上就是车辆非线性动力学模型。路面摩擦系数 μ \mu μ为路面固有信息,滑移率 s s s的控制需要由另一套控制系统来控制(ABS),在此我们假设此控制系统已经很好,滑移率 s s s就是一个已知量。
总结
以上三个模型都是常用的车辆模型,但是每个都有不同的用处以及不足,实际应用运动学和动力学要求都必须考虑到,当然,车速很低的情况下,需要考虑的因素较少,实践出真理,现有的MPC控制算法证明已经是可行的方案,唯一的缺陷就是MPC一旦预测步长过多,对算力的要求比较高。因此,模型的简化和算力之间的平衡,需要实际情况实际考虑,在此就不赘述了。