《基于数字信号处理的相干光通信技术》读书笔记chapter III——单载波相干检测及其关键技术
文章目录
- 相干光通信
- 单载波相干探测基本原理
- 使用偏振和相位分集接收的相干检测系统
- 相位分集接收的零差相干系统
- 基于相位分集和偏振分集的零差相干系统
- 数字信号处理基本流程
- 正交化与归一化
- Gram-Schmidt正交化过程(GSOP)
- Lowdin正交化过程
- 时钟恢复
- 数字滤波平方定时估计算法(前馈式)
- Gardner算法(反馈式)
- Godard算法
- Muller算法
- 反馈式全数字时钟同步方案
- 色散效应对传统时钟恢复算法的影响
- 色散补偿与静态平衡
- 光纤线性损耗补偿的结构
- 光纤色散的补偿算法
- 偏振动态信道均衡算法
- 恒模算法(CMA)
- 半径指向算法(RDA)
- 级联多模算法(CMMA)
- 问题及解决
- QPSK频偏估计与载波相位恢复
- 基于VV算法的前馈载波恢复
- 16QAM载波恢复算法
- 盲相位搜索算法(BPS)
- 改进的盲相位搜索算法(BPS/ML)
- QPSK分割与最大似然相结合的新型分割算法
发射机发送的光信号在经光纤传输后存在幅度的衰减和由于光纤线性与非线性效应导致的信号畸变。光接收机的作用,主要是探测经传输后的光信号并以此为基础完成对原始发射信号的恢复再生。
相干光通信
直接检测:WDM和EDFA技术,只有强度可以用来调制信息,结构简单且实现成本低。
相干检测:偏振复用技术,高阶的幅度/相位调制格式的使用和数字信号处理的应用大大提高了系统的频谱效率。
单载波相干探测基本原理
调制后的光信号
E S ( t ) = A S exp ( j ω s t ) E_{\rm{S}}(t)=A_{\rm{S}}\exp(j\omega_st) ES(t)=ASexp(jωst)
P S = ∣ A S ∣ 2 / 2 P_{\rm{S}}=|A_{\rm{S}}|^2/2 PS=∣AS∣2/2
接收端的本地LO
E L O ( t ) = A L O exp ( j ω s t ) E_{\rm{LO}}(t)=A_{\rm{LO}}\exp(j\omega_st) ELO(t)=ALOexp(jωst)
P L O = ∣ A L O ∣ 2 / 2 P_{\rm{LO}}=|A_{\rm{LO}}|^2/2 PLO=∣ALO∣2/2
使用平衡检测的方式

E 1 ( t ) = 1 2 ( E S + E L O ) E_1(t)=\frac{1}{\sqrt2}(E_{\rm{S}}+E_{\rm{LO}}) E1(t)=21(ES+ELO)
E 2 ( t ) = 1 2 ( E S − E L O ) E_2(t)=\frac{1}{\sqrt2}(E_{\rm{S}}-E_{\rm{LO}}) E2(t)=21(ES−ELO)
经过光电检测后,从两个PD输出的电流为 I 1 ( t ) I_1(t) I1(t)和 I 2 ( t ) I_2(t) I2(t)。
最终的平衡检测电流输出为:
I ( t ) = I 1 ( t ) − I 2 ( t ) = 2 R P S ( t ) P L O cos { ω I F ( t ) + θ s i g ( t ) − θ L O ( t ) } I(t)=I_1(t)-I_2(t)=2R\sqrt{P_{\rm{S}}(t)P_{\rm{LO}}}\cos \{ \omega_{\rm{IF}}(t)+\theta_{\rm{sig}}(t)-\theta_{\rm{LO}}(t) \} I(t)=I1(t)−I2(t)=2RPS(t)PLOcos{ωIF(t)+θsig(t)−θLO(t)}
| 条件 | 经平衡检测 | 系统要求的带宽 | 对于一个偏振态的QAM调制需要平衡检测器的个数 | 是否需要前置滤波器滤除信号的虚边带 | |
|---|---|---|---|---|---|
| 零差相干检测 | ω I F = ω S − ω L O = 0 \omega\rm_{IF}=\omega\rm_{S}-\omega\rm_{LO}=0 ωIF=ωS−ωLO=0 | 变成基带信号 | 发送端传输的基带信号带宽 B W BW BW | 2 | 是 |
| 外差相干检测 | ω I F = ω S − ω L O ≠ 0 \omega\rm_{IF}=\omega\rm_{S}-\omega\rm_{LO}\neq0 ωIF=ωS−ωLO=0 | 信号处在中频,需要电域的下变频变成基带信号 | B W + ω I F BW+\omega\rm_{IF} BW+ωIF,至少为 2 B W 2BW 2BW | 1 | 否 |
使用偏振和相位分集接收的相干检测系统
相位分集接收的零差相干系统

如图所示,从两对平衡接收机转换得到的同相分量为 I I ( t ) = I I 1 ( t ) − I I 2 ( t ) I_I(t)=I_{\rm{I1}}(t)-I_{\rm{I2}}(t) II(t)=II1(t)−II2(t)
正交分量为 I Q ( t ) = I Q 1 ( t ) − I Q 2 ( t ) I_Q(t)=I_{\rm{Q1}}(t)-I_{\rm{Q2}}(t) IQ(t)=IQ1(t)−IQ2(t)最终输出的信号为 I C ( t ) = I I ( t ) + j I Q ( t ) = R P S ( t ) P L O exp { j θ s ( t ) + θ n ( t ) } I_C(t)=I_{\rm{I}}(t)+jI_{\rm{Q}}(t)= R\sqrt{P_{\rm{S}}(t)P_{\rm{LO}}}\exp \{ \rm{j}\theta_{\rm{s}}(t)+\theta_{\rm{n}}(t) \} IC(t)=II(t)+jIQ(t)=RPS(t)PLOexp{jθs(t)+θn(t)}
这表明最终接收到的信号和传输信号之间的唯一差别在于引入了相位噪声 θ n ( t ) \theta_{\rm{n}}(t) θn(t),最常见的是基于接收机的数字信号处理技术来实现对相位噪声的估计和消除。
基于相位分集和偏振分集的零差相干系统
为了增加系统的频谱效率,可以提高系统中传输信号的调制阶数,还可以选择采用偏振复用来实现扩容。采用偏振分集接收的系统相对于单偏振方向的传输系统其频谱效率提高一倍。
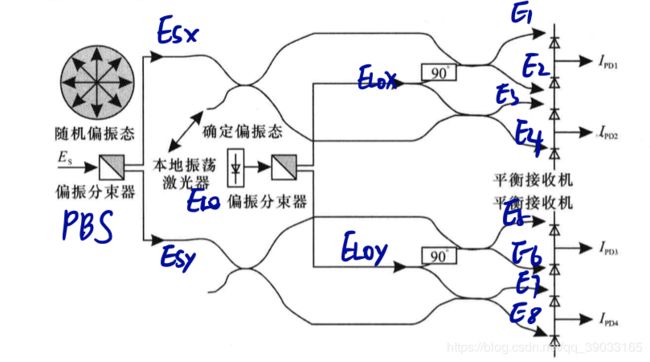
上图中,90°光混频器作用是实现单偏振的相位分集接收,信号 E S E_{\rm{S}} ES和 E L O E_{\rm{LO}} ELO经过PBS后被分为两个完全正交的偏振态信号。4对平衡检测器光电转换后的电流分别为 I P D 1 , 2 … 4 I_{\rm{PD1,2\ldots4}} IPD1,2…4,两个偏振态的信号则可以分别表示为 I x c ( t ) = I P D 1 ( t ) + j I P D 2 ( t ) I_{\rm{xc}}(t)=I_{\rm{PD1}}(t)+\rm{j}I_{\rm{PD2}}(t) Ixc(t)=IPD1(t)+jIPD2(t)
I y c ( t ) = I P D 3 ( t ) + j I P D 4 ( t ) I_{\rm{yc}}(t)=I_{\rm{PD3}}(t)+\rm{j}I_{\rm{PD4}}(t) Iyc(t)=IPD3(t)+jIPD4(t)
通过偏振耦合器就可以得到传输的信号。
数字信号处理基本流程
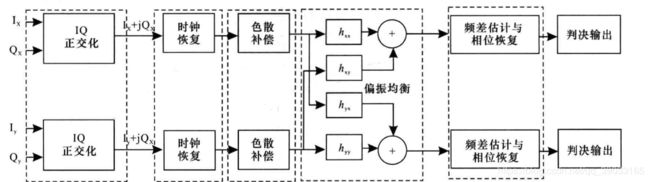
- 对接收信号进行正交化与归一化处理模块
IQ不平衡现象(I路和Q路信号之间幅度和相位失配,从而破坏I、Q两路的正交性,使得系统性能恶化)会对接收信号星座点产生影响。同时,实际相位分集接收机很容易受到不完美的光90°混频器的影响,导致在接收信号中的直流偏置以及幅度和相位误差。目的是补偿IQ不平衡现象。同时还要采用归一化处理来补偿光电探测器的响应度变化。
相位失配因子 θ \theta θ使得接收到的Q路中的数据混入了I路信息,混入的信息量随 θ \theta θ的变化而变化。当正交不平衡的相位失配因子 θ ≥ 30 ° \theta\geq30° θ≥30°和幅度失配因子 α ≥ 3 d B \alpha\geq3\rm{dB} α≥3dB时,系统BER明显恶化,系统需要响应的DSP算法补偿正交不平衡带来的信号失真。 - 时钟恢复模块
每路偏振光的两路正交连续电信号在输入到DSP处理单元之前经过ADC进行采样量化,ADC的采样时钟由本地时钟提供,使得收发端时钟存在频率偏移与相位抖动。由于受到光纤信道损耗如色散、偏振膜色散等因素的综合影响,发端与ADC时钟间的频率偏移比较大,得到的采样序列将存在一个累积的频率与相位定时误差,导致BER性能恶化。目的是消除ADC采样时钟不匹配造成的时钟未校准以及采样时钟的相位抖动。 - 色散补偿和偏振均衡模块
光纤色散会造成信道静态损伤以及偏振模色散将对接收信号造成影响。
光相干接收机前端PBS引入偏振旋转造成接收信号存在偏振串扰的影响。 - 频差估计与相位恢复模块
本振光源与发端激光器之前存在频差,激光器的线宽也会引入相位偏移,使相干检测后的信号中附加了大量的相位噪声。造成接收信号星座点的旋转发散。载波恢复模块首先利用载波频偏估计算法对频偏进行补偿,再借助载波相位估计算法对本振光源线宽及残留频偏引起的相偏进一步修正。
正交化与归一化
Gram-Schmidt正交化过程(GSOP)
能够将不满足正交性的采样值转化为一系列正交的采样值,从而恢复I、Q采样序列的正交性。 I o u t = r I ( t ) P I I_{\rm{out}}=\frac{r_I(t)}{\sqrt{P_{\rm{I}}}} Iout=PIrI(t)
Q ′ ( t ) = r Q ( t ) − ρ r I ( t ) P I Q'(t)=r_Q(t)-\frac{\rho r_I(t)}{\sqrt{P_{\rm{I}}}} Q′(t)=rQ(t)−PIρrI(t)
Q o u t = Q ′ ( t ) P Q Q_{\rm{out}}=\frac{Q'(t)}{\sqrt{P_{\rm{Q}}}} Qout=PQQ′(t)
其中, r I ( t ) r_I(t) rI(t)和 r Q ( t ) r_Q(t) rQ(t)表示接收信号的非正交IQ分量,而 I o u t ( t ) I_{\rm{out}}(t) Iout(t)和 Q o u t ( t ) Q_{\rm{out}}(t) Qout(t)则表示经过GSOP算法处理后的正交IQ分量。
GSOP算法对相位失配问题的理论补偿范围为 ( − 90 ° , + 90 ° ) (-90°,+90°) (−90°,+90°),对幅度失配问题的补偿为 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞),但由于实际中存在的噪声、色散等影响因素的存在,GSOP算法相位失配的补偿范围为 ± 60 ° \pm60° ±60°之间。
在接收端采用分辨率为4bit或5bit的GSOP算法时,正交不平衡带来的系统性能损伤能够完好地恢复(OSNR损失接近0)。
Lowdin正交化过程
GSOP算法增加了量化噪声对接收信号的影响。Lowdin正交化过程采用对称的正交化方法。随着高阶调制格式带来的谱密度增加,采用Lowdin正交化方法来代替传统的GSOP方法可以进一步提高系统性能。
时钟恢复

其中: x ( t ) x(t) x(t)为接收到经正交化与归一化处理后的信号;
x ( m T s ) x(mT_{\rm{s}}) x(mTs)为接收端本地时钟采样得到的异步采样序列
y ( k T i ) y(kT_{\rm{i}}) y(kTi)为经过时钟同步后输出的同步采样序列
定时误差检测:采用线性的定时误差检测算法,能够直接准确地计算当前定时误差的大小。但由于实时性的要求,该算法计算复杂度较高,且还需对每符号至少采样4次,对于高速的传输系统将很难实现。
差值滤波器:根据当前误差进行定时调整,具有同步建立快和全数字化实现的优点。

特点:存在反馈结构引入的延迟,对时钟抖动追踪能力有限。但是无需严格的线性定时误差检测且算法实现较为简单,每符号只采样2次。模拟器件还有漂移和容差等不理想特性。
数字滤波平方定时估计算法(前馈式)
对光纤传输损耗引起的波形失真和载波相位不敏感,但受限于其平方运算计算复杂度和采样速率高(4倍符号速率以上的采样速率),因此在高速传输系统中的应用有限。
Gardner算法(反馈式)
对符号 I ( n ) I(n) I(n)的两次采样时刻为当前符号 I ( n ) I(n) I(n)时刻以及中间时刻 I ( n − 1 / 2 ) I(n-1/2) I(n−1/2)。通过中间时刻采样值的幅值和大小确定最终的定时误差大小。

对第 r r r个符号的同向和正交分量采样两次,得到定时差错判决表达式: ξ ( r ) = y I ( r − 1 / 2 ) [ y I ( r ) − y I ( r − 1 ) ] + y Q ( r − 1 / 2 ) [ y Q ( r ) − y Q ( r − 1 ) ] \xi(r)=\rm{y}_{\rm{I}}(r-1/2)[\rm{y}_{\rm{I}}(r)-\rm{y}_{\rm{I}}(r-1)]+ \rm{y}_{\rm{Q}}(r-1/2)[\rm{y}_{\rm{Q}}(r)-\rm{y}_{\rm{Q}}(r-1)] ξ(r)=yI(r−1/2)[yI(r)−yI(r−1)]+yQ(r−1/2)[yQ(r)−yQ(r−1)]
Godard算法
从有效控制和避免频谱交叠引起干扰的角度出发,提出了一种衡量接收端采样时钟相位 τ \tau τ的判定标准。根据能量最大化原则(通过使包含在采样脉冲中的采样时钟相位 τ \tau τ的能量最大进而降低由符号频谱交叠引起的干扰)确定初始相位后,再引入迭代梯度搜索算法使得时钟控制信号自动地调整最终达到全局最优。
Muller算法
基于采样时钟相位 τ \tau τ的定义提出了一种时间函数 f ( τ ) f(\tau) f(τ)的定义,利用采样信号 x k x_{\rm{k}} xk的线性组合 g k T x k g_{\rm{k}}^\mathrm{T}x_{\rm{k}} gkTxk 构造参数 z k = g k T x k z_{\rm{k}}=g_{\rm{k}}^\mathrm{T}x_{\rm{k}} zk=gkTxk 。通过调整权重系数 g k g_{\rm{k}} gk,使得参数 z k z_{\rm{k}} zk的期望和 f ( τ ) f(\tau) f(τ)相等且方差最小,实现对 f ( τ ) f(\tau) f(τ)的无偏估计。
反馈式全数字时钟同步方案
通过数字插值的方式实现定时调整,恢复出同步采样序列。全数字的实现方式有效避免了传统反馈式混合时钟方案中模拟器件漂移、容差等不理想特性。仅需提供时钟恢复定时调整的方向和趋势,无需如传统前馈式全数字时钟同步算法中需实时计算当前定时误差精确值的高计算复杂度问题,具有实现成本低、易制造的显著特点。
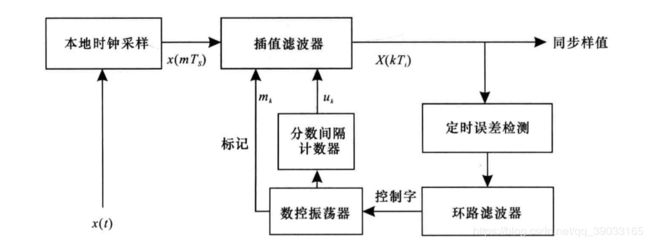
- 实现过程
插值滤波器:根据控制单元提供的控制信息对异步采样序列进行定时调整,插值处理后的采样值被进行定时误差检测;定时误差检测器采用Gardner算法,提供同步环路调整的方向和趋势。检测出的误差信号经过比例加积分环路滤波器滤除噪声后形成控制字 W ( n ) W(n) W(n)提供给数控振荡器(NCO),再输出参数 m k m_{\rm{k}} mk和 u k u_{\rm{k}} uk,然后提供给插值滤波器进行定时调整,使环路逐步建立同步。 - 插值滤波器
利用接收异步采样序列 x ( m T s ) x(mT_{\rm{s}}) x(mTs),先经插值滤波器还原成 X ( t ) X(t) X(t),之后重新采样输出同步后的序列 x ( k T i ) x(kT_{\rm{i}}) x(kTi),完成采样速率转换的过程。还原采用了拉格朗日立方插值滤波器,对于某一内插点 X ( k T i ) X(kT{\rm{i}}) X(kTi)需要选择4个基本样点: x [ ( m k − 2 ) T s ] x[(m_{\rm{k}}-2)T_{\rm{s}}] x[(mk−2)Ts]、 x [ ( m k − 1 ) T s ] x[(m_{\rm{k}}-1)T_{\rm{s}}] x[(mk−1)Ts]、 x [ ( m k ) T s ] x[(m_{\rm{k}})T_{\rm{s}}] x[(mk)Ts]、 x [ ( m k + 1 ) T s ] x[(m_{\rm{k}}+1)T_{\rm{s}}] x[(mk+1)Ts]。信号在这段时间内的波形曲线有: X ( t ) = x ( m k − 2 ) C − 2 + x ( m k − 1 ) C − 1 + x ( m k ) C 0 + x ( m k + 1 ) C 1 X(t)=x(m_{\rm{k}}-2)C_{-2}+x(m_{\rm{k}}-1)C_{-1}+x(m_{\rm{k}})C_{0}+x(m_{\rm{k}}+1)C_{1} X(t)=x(mk−2)C−2+x(mk−1)C−1+x(mk)C0+x(mk+1)C1其中 C − 2 = − 1 6 u k 3 + 1 6 u k C_{-2}=-\frac{1}{6}u_k^3+\frac{1}{6}u_k C−2=−61uk3+61uk, C − 1 = 1 2 u k 3 + 1 2 u k 2 − u k C_{-1}=\frac{1}{2}u_k^3+\frac{1}{2}u_k^2-u_k C−1=21uk3+21uk2−uk, C 0 = − 1 2 u k 3 − u k 2 + 1 2 u k + 1 C_{0}=-\frac{1}{2}u_k^3-u_k^2+\frac{1}{2}u_k+1 C0=−21uk3−uk2+21uk+1, C 1 = 1 6 u k 3 + 1 2 u k 2 + 1 3 u k C_{1}=\frac{1}{6}u_k^3+\frac{1}{2}u_k^2+\frac{1}{3}u_k C1=61uk3+21uk2+31uk
色散效应对传统时钟恢复算法的影响
- 影响
在光纤色散的影响下,接收信号的频谱 R ( f ) R(f) R(f)与发射信号 S ( f ) S(f) S(f)间关系为:
R ( f ) = H C D ( f ) S ( f ) e j 2 π f τ s R(f)=H_{\rm{CD}}(f)S(f)e^{j2\pi f\tau_s} R(f)=HCD(f)S(f)ej2πfτs
其中, H C D ( f ) H_{\rm{CD}}(f) HCD(f)为光纤色散传输函数, τ s \tau_s τs为实际发送信号与ADC采样时钟间的时钟偏移。
R ( f ) R(f) R(f)的自相关函数的幅值近似为频域显示的采样时钟信息幅度,可得 ∣ C ( f s , B ) ∣ = ∣ sin ( ψ 2 B f s ) ψ 4 f s S ( B / 2 − f s ) S ∗ ( B / 2 − f s ) ∣ |C(f_s,B)|=\left|\frac{\sin(\psi2Bf_s)}{\psi4f_s}S(B/2-f_s)S^*(B/2-f_s)\right| ∣C(fs,B)∣=∣∣∣∣ψ4fssin(ψ2Bfs)S(B/2−fs)S∗(B/2−fs)∣∣∣∣
当色散程度 ψ \psi ψ较小时, ∣ C ( f s , B ) ∣ |C(f_s,B)| ∣C(fs,B)∣主要受到预滤波器带宽B的影响;当B固定时,采样函数包络同色散效应 ψ \psi ψ 的倒数成正比,也即当残余色散值偏大时采样时钟信息会受到明显影响。一旦时钟信息的幅度减小到与噪声幅度相当时将无法通过时钟恢复算法对始终信息进行提取与恢复。 - 解决
- 优化B;
- 将色散估计与补偿模块提前到时钟恢复模块之前来保证时钟恢复算法的性能;
- 将蝶形CD,PMD补偿均衡器融合到时钟恢复模块中,提高其抗色散能力;
- 改善时钟恢复算法本身对色散抵抗能力
色散补偿与静态平衡
色散:在光纤中传输的信号由于含有不同的频率或模式成分,经光纤传输后的信号脉冲会因群速度不同展宽,引起信号失真。
影响:使得传输的信号脉冲产生畸变,限制了光纤的传输容量和传输带宽。
解决:采用基于色散补偿光纤的(DCF)光补偿或者数字信号处理算法的非光补偿方式,后者相较而言成本低且对光纤非线性效应的容忍度更高。
需要对光纤传输引入损耗(包括线性与非线性损耗)进行补偿。为了简化相干接收机的结构,在下面的讨论中忽略非线性损耗,仅考虑如色度色散(CD)、偏振膜色散(PMD)等光纤线性损耗。
光纤线性损耗补偿的结构

- 单层纯蝶形结构
4个自适应FIR滤波器组成,同时对CD和PMD补偿 - 双层结构
第一层针对CD进行补偿,第二层对于偏振相关的损耗如偏振旋转、偏振膜色散进行补偿。模块内部前后两个子模块可以分别运行于不同的速率,为数字信号处理的实现带来了极大的便利,简化了系统的计算复杂度。
光纤色散的补偿算法
- 光纤色散效应的数学表示: β ( ω ) = n ( ω ) ω c = β 0 + β 1 ( ω − ω 0 ) + 1 2 β 2 ( ω − ω 0 ) 2 + Λ , β m = ( d m β d ω m ) ω = ω 0 ( m = 0 , 1 , 2 … ) \beta(\omega)=n(\omega)\frac{\omega}{c}=\beta_0+\beta_1(\omega-\omega_0)+\frac{1}{2}\beta_2(\omega-\omega_0)^2+\Lambda,\beta_m=(\frac{d^m\beta}{d\omega^m})_{\omega=\omega_0}(m=0,1,2\ldots) β(ω)=n(ω)cω=β0+β1(ω−ω0)+21β2(ω−ω0)2+Λ,βm=(dωmdmβ)ω=ω0(m=0,1,2…)
- 对光纤色散引起的脉冲展宽的程度进行量化: Δ T = D ⋅ ξ λ ⋅ L \Delta T=D\cdot\xi \lambda\cdot L ΔT=D⋅ξλ⋅L
即带宽为 ξ λ \xi \lambda ξλ的光信号脉冲经过 L L L长的光纤传输后脉冲展宽的程度 Δ T \Delta T ΔT. - 光纤色散对信号包络 U ( z , τ ) U(z,\tau) U(z,τ)影响的偏微分方程: ∂ U ( z , τ ) ∂ z = − j 2 ( − D λ 2 2 π c ) ∂ 2 U ( z , τ ) ∂ τ 2 = j D λ 2 4 π c ∂ 2 U ( z , τ ) ∂ τ 2 \frac{\partial U(z,\tau)}{\partial z}=-\frac{\rm{j}}{2}(\frac{-D \lambda^2 }{2\pi c})\frac{\partial^2U(z,\tau)}{\partial \tau^2}=\rm{j}\frac{D\lambda ^2}{4\pi c}\frac{\partial ^2U(z,\tau)}{\partial \tau^2} ∂z∂U(z,τ)=−2j(2πc−Dλ2)∂τ2∂2U(z,τ)=j4πcDλ2∂τ2∂2U(z,τ)
是所有光纤色散补偿算法的基础,其中 z z z表示传输距离, τ \tau τ表示归一化时间参量, D D D表示光纤的色散系数, λ \lambda λ表示光波波长, c c c表示光速。 - 频域均衡算法
对上式进行傅里叶变换(FFT)得到频域传输方程为: G ( z , w ) = exp ( − j D λ 2 4 π c ω 2 ) G(z,w)=\exp(-\rm{j}\frac{D\lambda ^2}{4\pi c}\omega^2) G(z,w)=exp(−j4πcDλ2ω2)
一般采用FIR滤波器 1 / G ( z , w ) 1/G(z,w) 1/G(z,w)实现在频域对色散的直接补偿,其频域传递函数为: G ( z , w ) = exp ( j D λ 2 4 π c ω 2 ) G(z,w)=\exp(\rm{j}\frac{D\lambda ^2}{4\pi c}\omega^2) G(z,w)=exp(j4πcDλ2ω2)
频域色散补偿具体实现过程为:将接收到的时域信号截断为若干块,对每一子块做FFT变换到频域,接着直接在频域与频域传递函数相乘得到色散补偿的频域信号,接着做IFFT运算变换回时域。 - 时域均衡算法
对上式进行进一步傅里叶变换得到时域冲击响应:
g ( z , t ) = c j D λ 2 z exp ( j π c D λ 2 z t 2 ) g(z,t)=\sqrt{\frac{c}{\rm{j}D\lambda^2z}}\exp(\rm{j}\frac{\pi c}{D\lambda ^2z}t^2) g(z,t)=jDλ2zcexp(jDλ2zπct2)
因此也可对光纤色散进行时域补偿。
滤波器总抽头数为N,抽头的权重由下式给出: a k = j c T 2 D λ 2 z exp ( − j π c T 2 D λ 2 z k 2 ) ⌈ N 2 ≤ k ≤ ⌈ N 2 ⌉ N = 2 ⋅ ⌈ ∣ D λ 2 z ∣ 2 c T 2 ⌉ + 1 a_k=\sqrt{\frac{\rm{jcT^2}}{D\lambda^2z}}\exp(-\rm{j}\frac{\pi cT^2}{D\lambda^2z}k^2) \lceil\frac{N}{2}\leq k \leq\lceil\frac{N}{2}\rceil N =2\cdot\lceil \frac{|D\lambda^2z|}{2cT^2}\rceil+1 ak=Dλ2zjcT2exp(−jDλ2zπcT2k2)⌈2N≤k≤⌈2N⌉N=2⋅⌈2cT2∣Dλ2z∣⌉+1
对滤波器抽头权重给出了简单的闭区间解,也给出了算法所需抽头数量的上界。抽头数采用最大截断窗口长度时,权重是最优的,色散补偿的效果也最好。在实际中要对最大滤波器抽头数进一步截断,权重次优,但为系统实现复杂度进一步优化提供了可能。 - 两类均衡算法的性能比较
- 性能比较
当N>300时,随光纤色散程度的加剧引起OSNR劣化都很小;
当N较小时,时域均衡算法的劣化远大于频域。也即为达到相近的系统性能时域滤波器所需的抽头数一般小于频域均衡滤波器。 - 计算复杂度比较
频域均衡算法在色散近似为11000ps/nm(40Bbit/s系统)和2000ps/nm(100Gbit/s系统)时计算复杂度陡增,随着色散的增加整体趋势趋于平缓;时域均衡算法的复杂度仅在色散较弱的小范围内低于频域均衡,随着色散成都增加整体趋势快速增大,与符号速率平方成正比。
- 性能比较
偏振动态信道均衡算法
- 差分群延迟
在单模光纤中,基模是由两个相互正交的偏振膜 H E 11 x HE_{11}^x HE11x和 H E 11 y HE_{11}^y HE11y组成的,两个偏振膜完全简并,具有相同的传播速度,不存在时延差的现象。实际中,由于生产工艺和机械外力的作用导致光纤沿不同的方向有着不同的有效折射率,导致光纤的双折射,造成两个正交偏振模传播常数的差异,形成时延差,即差分群延迟。 - 随机模式耦合
随时间和波长变化 - 偏振膜色散的补偿
偏振模色散(PMD)成为限制系统比特距离积的首要因素,通常采用恒模算法(CMA)在电域上对偏振模色散进行补偿。一般采用4个蝶形自适应滤波器实现偏振恢复和解复用、偏振模色散补偿和残余色散补偿。对于这种快速自适应均衡,一般使用经典随机梯度算法进行均衡器的抽头系数更新。在这之前,要先选择一个代价函数描述均衡器输出信号的误差程度并反馈到均衡器以更新系数。
选择函数 G ( p ) G^{(p)} G(p), G ( p ) = E ( ∣ z n ∣ p − ∣ a n ∣ p ) 2 G^{(p)}=E(|z_n|^p-|a_n|^p)^2 G(p)=E(∣zn∣p−∣an∣p)2作为代价函数来表示信号误差,最小化 G ( p ) G^{(p)} G(p)就可以使偏振模色散最小化。
恒模算法(CMA)
D ( 2 ) = E ∣ a n ∣ 4 ( 1 − ∣ s 0 ∣ 2 ) 2 + E ∣ a n ∣ 4 ∑ k ′ ∣ s k ∣ 4 + 2 ( E ∣ a n ∣ 2 ) 2 { ( ∑ k ′ ∣ s k ∣ 2 ) 2 − ∑ k ′ ∣ s k ∣ 4 } + { 4 ( E ∣ a n ∣ 2 ) 2 ∣ s 0 ∣ 2 − 2 E ∣ a n ∣ 4 } ∑ k ′ ∣ s k ∣ 2 + R 2 2 − E ∣ a n ∣ 4 \begin{aligned} D^{(2)}=& E\left|a_{n}\right|^{4}\left(1-\left|s_{0}\right|^{2}\right)^{2}+E\left|a_{n}\right|^{4} \sum_{k}{\prime}\left|s_{k}\right|^{4}+2\left(E\left|a_{n}\right|^{2}\right)^{2}\left\{\left(\sum_{k}{\prime}\left|s_{k}\right|^{2}\right)^{2}-\sum_{k}{\prime}\left|s_{k}\right|^{4}\right\} +\left\{4\left(E\left|a_{n}\right|^{2}\right)^{2}\left|s_{0}\right|^{2}-\left.2 E\left|a_{n}\right|^{4}\right\}\sum_{k}{\prime}\left| s_{k}\right|^{2}+R_{2}^{2}-E\left|a_{n}\right|^{4}\right.\end{aligned} D(2)=E∣an∣4(1−∣s0∣2)2+E∣an∣4k∑′∣sk∣4+2(E∣an∣2)2⎩⎨⎧(k∑′∣sk∣2)2−k∑′∣sk∣4⎭⎬⎫+{4(E∣an∣2)2∣s0∣2−2E∣an∣4}k∑′∣sk∣2+R22−E∣an∣4
尤其适用于恒定幅度的调制格式,如M阶相移键控;对于幅度不恒定的调制格式QAM,算法的时间平均误差无法减小到0,因为均衡之后会引入额外的噪声。故提出了以下几种算法。
半径指向算法(RDA)
用于16QAM调制格式
根据该点距原点的距离判断它最可能属于的环,并根据所属的环半径计算误差。
级联多模算法(CMMA)
用于8QAM和16QAM调制格式
通过级联的方式引入多个参考圆环,由随机梯度算法可得出8QAM/16QAM调制格式的相应滤波器抽头权重系数更新方程。
问题及解决
对SNR性能有提高,但是由于依赖于对发射信号半径的正确判断也降低了滤波器收敛过程的鲁棒性。
- 先使用CMA算法进行预收敛,再选择一种多模算法进行处理。对高阶QAM调制(如32QAM和64QAM),使用多模算法偏振解复用的复杂度很高,选择两或者三个内环进行误差反馈计算来降低复杂度。
- 先CMA进行预收敛,接下来使用判决辅助最小均方算法(DD-LMS)进行误差计算。判决辅助最小均方算法的误差计算公式如下: ϵ x , y ( i ) = Z x , y ( i ) − d x , y ( i ) \epsilon_{\rm{x,y}}(i)=Z_{\rm{x,y}}(i)-d_{\rm{x,y}}(i) ϵx,y(i)=Zx,y(i)−dx,y(i)其中 d x , y ( i ) d_{\rm{x,y}}(i) dx,y(i)是在载波频率和相位恢复之后进行基于最佳QAM判决边界判决的最终信号。接下来进行滤波器抽头系数更新。
CMA/DD-LMS算法需要将均衡和载波恢复以及判决在一个功能模块/循环中实现,CMA预均衡引起的残余相位噪声较大会使DD-LMS算法失败。- 改进的DD-LMS算法
使用与相位无关的误差信号计算: ϵ x , y ( i ) = ∣ Z x , y ( i ) ∣ 2 − ∣ d x , y ( i ) ∣ 2 \epsilon_{\rm{x,y}}(i)=|Z_{\rm{x,y}}(i)|^2-|d_{\rm{x,y}}(i)|^2 ϵx,y(i)=∣Zx,y(i)∣2−∣dx,y(i)∣2
误差的计算仅基于半径信息,类似RDA。但RDA半径的判决是基于环的边界,但该算法是在载波频率和相位恢复之后基于最佳QAM判决边界进行半径判断。
- 改进的DD-LMS算法
QPSK频偏估计与载波相位恢复
基于数字锁相环(PLL)的判决辅助和判决反馈机制被广泛用于射频通信系统中的载波相位恢复。而在高速光通信系统中,光载波的相位变化速度远快于射频载波,只有使用基于前馈的相位恢复才能在实际中通过并行处理和流水线结构实现。频率偏移变化速度缓慢,PLL可以在高速光通信系统中用于发射机和本振激光器频率偏移的估计。
基于VV算法的前馈载波恢复
用于PSK调制格式的系统中,频偏估计必须在相位估计之前进行。由于频偏会引起相邻采样之间的相位差,只需要估计出连续采样之间的相位差就可以计算出频偏 △ v \bigtriangleup v △v。
- 移除频偏噪声
对于相位调制信号来说,接收到的第 n n n个信号码元为: S n = exp ( j ( a n + 2 π n △ v T S + θ n ) ) S_n=\exp(\rm{j} (a_n+2\pi n\bigtriangleup vT_S+\theta_n)) Sn=exp(j(an+2πn△vTS+θn))
其中, a n a_n an为原始信号相位, △ v \bigtriangleup v △v为发射机和本振激光器之间的频率偏差, T s T_{s} Ts为码元采样间隔, θ n \theta_n θn为激光器相位噪声。
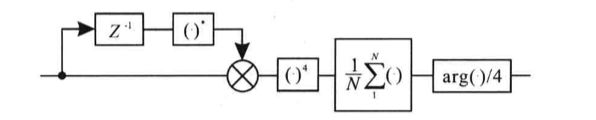
- 复数 d n d_n dn的相位是前后两个码元的相位差 d n = S n × S n − 1 ∗ = exp ( j ( a n − a n − 1 + △ φ + ( θ n − θ n − 1 ) ) ) d_n=S_n \times S_{n-1}^*=\exp(\rm{j}(a_n-a_{\rm{n-1}}+\bigtriangleup \varphi+(\theta_n-\theta_{n-1}))) dn=Sn×Sn−1∗=exp(j(an−an−1+△φ+(θn−θn−1)))
由于激光器的相位噪声变化不大,我们认为 θ n − θ n − 1 = 0 \theta_n-\theta_{n-1}=0 θn−θn−1=0,即 d n = exp ( j ( a n − a n − 1 + △ φ ) ) d_n=\exp(\rm{j}(a_n-a_{\rm{n-1}}+\bigtriangleup \varphi)) dn=exp(j(an−an−1+△φ)) - 移除信号相位中包含的编码信息(以QPSK信号为例)
d n 4 = exp ( j ( 4 b n + 4 △ φ ) ) = exp ( j 4 △ φ ) ) d_n^4=\exp(\rm{j}(4b_n+4\bigtriangleup \varphi))=\exp(\rm{j}4\bigtriangleup \varphi)) dn4=exp(j(4bn+4△φ))=exp(j4△φ)) - 将相邻10个数据累加后求平均值以消除突发误差
- 求平均值的相位,得到的相位除以4是相位差 △ φ \bigtriangleup \varphi △φ的估计值。
- 每个码元移除频偏引起的累积相位偏移补偿频偏的影响,得到无频偏影响的数据 S n ′ S_n' Sn′,并进行进一步的相位估计。
- 载波相位恢复
移除频偏噪声后的信号表达式为:
S n ′ = exp ( j ( a n + θ n ) ) S_n'=\exp(\rm{j}(a_n+\theta_n)) Sn′=exp(j(an+θn))

- M次方以移除相位调制信息
S n 4 ′ = exp ( j 4 ( a n + θ n ) ) {S_n^4}'=\exp(\rm{j}4(a_n+\theta_n)) Sn4′=exp(j4(an+θn)) - 得到载波相位估计值
由于光相位 θ \theta θ的变化速率对于光相位调制速率变化缓慢,因此对前后多个码元载波相位求平均获得相位估计。得到的复数的相位除以4就是载波相位估计值 θ e \theta_e θe。 - 解码
判断第 n n n个采样的相位 θ s = [ arg ( S n ′ ) − θ e ] \theta_s=[\arg(S_n')-\theta_e] θs=[arg(Sn′)−θe]在QPSK信号的编码区域中的位置就完成了解码。
16QAM载波恢复算法
盲相位搜索算法(BPS)
适用于任意 M M M阶QAM调制,BPS算法采用纯前馈结构

- 将含有相位噪声的采样符号 r k r_k rk用 B B B个测试相位 ϕ b \phi_b ϕb在星座图平面进行旋转,测试相位为: ϕ b = b B ⋅ π 2 \phi_b=\frac{b}{B}\cdot \frac{\pi}{2} ϕb=Bb⋅2π。其中, b b b取 − B / 2 -B/2 −B/2到 B / 2 − 1 B/2-1 B/2−1以修正正负相位噪声的影响。参数 B B B影响算法的精确度和计算量,对于16QAM信号取32为宜。
- 将经过旋转的符号输入判决电路,输出与输入符号距离最近的理想星座点 y ^ k , b \hat{y}_{k,b} y^k,b,进而计算平方距离。
- 将前后连续 2 N 2N 2N个星座点平方距离求和得: s k , b = ∑ n = − N N ∣ d k − n , b ∣ 2 s_{k,b}=\sum_{n=-N}^{N}|d_{k-n,b}|^2 sk,b=n=−N∑N∣dk−n,b∣2
- 在 B B B个星座点平方距离和中取最小值,选取与其对用的 y ^ k , b \hat{y}_{k,b} y^k,b作为 该算法对发射信号的判决 Y ^ k \hat{Y}_k Y^k,消除相位噪声的影响。
改进的盲相位搜索算法(BPS/ML)
- 第一级处理沿用BPS算法进行粗略估计(减小测试相位 ϕ b \phi_b ϕb的数量)以获得星座点最佳相位角的一个大致位置
- 第二级处理引入一个最大似然相位估计其改善第一级的估计精确性。
将原始接收符号 r k r_k rk和第一级输出 Y ^ k ( 1 ) \hat{Y}_k^{(1)} Y^k(1)共同输入最大似然相位估计其得第二级相位噪声的估计值 ϕ k M L \phi_k^{ML} ϕkML - 将重新经过相位纠正的信号 r k e − j ϕ k M L r_k\rm{e^{-\rm{j}\phi_k^{ML}}} rke−jϕkML输入判断电路得第二级的判决输出 Y ^ k ( 2 ) \hat{Y}_k^{(2)} Y^k(2)
- (可以在第二级后添加多个级联的最大似然估计相位单元来提高估计精确度……)
QPSK分割与最大似然相结合的新型分割算法
基于16QAM调制信号的星座图布局特点对星座点进行合理分割,结合经修正的VVPE算法以及最大似然相位估计,以更低的计算复杂度开销实现对16QAM信号的载波恢复。
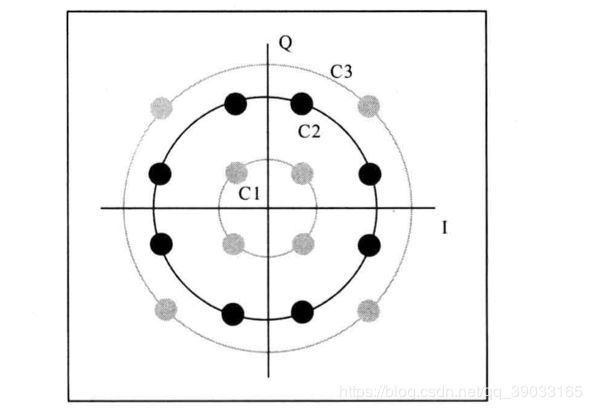

- 采用修正的VVPE算法对内圈和外圈的相位噪声进行估计
输入的 2 N 2N 2N个接收符号根据幅值进行分类与归一化处理,从中提取内圈 C 1 C_1 C1及外圈 C 3 C_3 C3的符号序列,算法过程如下式: θ n e s t 1 = 1 4 ⋅ { ∑ i : s i ∈ C 1 s i 4 ∣ s i 4 ∣ + W 1 ∑ i : s i ∈ C 3 s i 4 ∣ s i 4 ∣ } \theta_{n}^{e s t 1}=\frac{1}{4} \cdot\left\{\sum_{i: s_{i} \in C_{1}} \frac{s_{i}^{4}}{\left|s_{i}^{4}\right|}+W_{1} \sum_{i: s_{i} \in C_{3}} \frac{s_{i}^{4}}{\left|s_{i}^{4}\right|}\right\} θnest1=41⋅{i:si∈C1∑∣si4∣si4+W1i:si∈C3∑∣si4∣si4} - 对 C 2 C_2 C2的符号根据粗估计值 θ n e s t 1 \theta_n^{est1} θnest1进行补偿并输入到第一个最大似然相位估计器中,得到残余的相位噪声 θ n e s t 2 \theta_n^{est2} θnest2,故更精确的相位噪声为: θ n e s t = θ n e s t 1 + θ n e s t 2 \theta_n^{est}=\theta_n^{est1}+\theta_n^{est2} θnest=θnest1+θnest2,作为第一阶段相位噪声的估计值。
- 对分布在 C 1 C_1 C1, C 2 C_2 C2, C 3 C_3 C3上的所有星座点乘以 e − j θ n e s t e^{-\rm{j}\theta_n^{est}} e−jθnest做修正得 x n x_n xn
- 将第一阶段修正的结果 x n x_n xn输入到第二阶段的最大似然相位估计器中,得到第二阶段的相位噪声估计值 θ n M L = tan − 1 ( lm [ h n ] / Re [ h n ] ) , h n = ∑ k = n − M + 1 n + M x k ⋅ y ^ k ∗ \theta_{n}^{ML}=\tan ^{-1}\left(\operatorname{lm}\left[h_{n}\right] / \operatorname{Re}\left[h_{n}\right]\right), h_{n}=\sum_{k=n-M+1}^{n+M} x_{k} \cdot \hat{y}_{k}^* θnML=tan−1(lm[hn]/Re[hn]),hn=k=n−M+1∑n+Mxk⋅y^k∗
- 输出最终经相位噪声补偿的符号为: x n ′ = x n e − j θ n M L x_n'=x_n\rm{e}^{\rm{-j}\theta_n^{ML}} xn′=xne−jθnML