MST——最小生成树模板
题目描述:
给定一个无向图,每条边有一个非负权值。求这个图中最小生成树的所有边的权值之和。生成树是指包含图中所有节点的一棵树,而最小生成树则指一棵所有边的权值之和最小的生成树。
输入:
第一行包含两个数,n和m,其中n为节点数,m为边数。下面m行,每行三个非负整数a、b和c,a, b
输出一个数,表示一棵最小生成树所有边的权值之和。
样例输入:
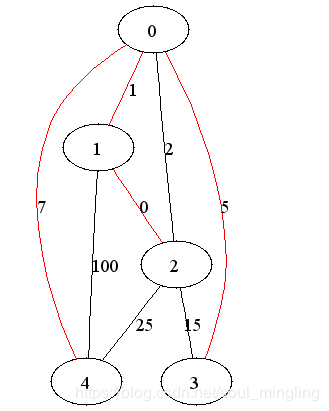
5 8
0 1 1
0 2 2
0 3 5
0 4 7
1 2 0
2 3 15
2 4 25
1 4 100
样例输出:
13
提示:
对于30%的数据,m≤10;
对于50%的数据,m≤1000;
对于100%的数据,m≤100000,c≤2000。
最小生成树模板题。(正文150行开始)
#pragma GCC optimize(3,"Ofast","inline")
#pragma G++ optimize(3)
#include::iterator
#define fs(n) fixed<< setprecision(n)
//const double e=2.71828182845;
const double pi = acos(-1.0);
void read(int &x)
{
char ch=getchar();
x=0;
for(; ch<'0'||ch>'9'; ch=getchar());
for(; ch>='0'&&ch<='9'; x=x*10+ch-'0',ch=getchar());
}
inline void write(ll x)
{
if(x<0)
putchar('-'),x=-x;
if(x>9)
write(x/10);
putchar(x%10+'0');
}
float SqrtByCarmack( float number )
{
int i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( int * ) &y;
i = 0x5f375a86 - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) );
y = y * ( threehalfs - ( x2 * y * y ) );
y = y * ( threehalfs - ( x2 * y * y ) );
return number*y;
}
ll qpow(ll a,ll b,ll mod)
{
ll sum=1;
while(b)
{
if(b%2==1)
{
sum=sum*a%mod;
}
b/=2;
a=a*a%mod;
}
return sum;
}
int erfen(int *a,int start,int endd,int l)//小于等于l的最大值的角标
{
int mid=(start+endd)/2;
if((a[mid]<=l&&a[mid+1]>l)||(mid==endd&&a[mid]<=l))
return mid;
else if(a[mid]<=l)
return erfen(a,mid+1,endd,l);
else if(a[mid]>l)
{
if(start!=mid)
return erfen(a,start,mid,l);
else
return start-1;
}
}
ll prime[6] = {2, 3, 5, 233, 331};
ll qmul(ll x, ll y, ll mod)
{
return (x * y - (long long)(x / (long double)mod * y + 1e-3) *mod + mod) % mod;
}
bool Miller_Rabin(ll p)
{
if(p < 2)
return 0;
if(p != 2 && p % 2 == 0)
return 0;
ll s = p - 1;
while(! (s & 1))
s >>= 1;
for(int i = 0; i < 5; ++i)
{
if(p == prime[i])
return 1;
ll t = s, m = qpow(prime[i], s, p);
while(t != p - 1 && m != 1 && m != p - 1)
{
m = qmul(m, m, p);
t <<= 1;
}
if(m != p - 1 && !(t & 1))
return 0;
}
return 1;
}
ll gcd(ll x,ll y)
{
if(y==0)
return x;
else
return gcd(y,x%y);
}
int fa[100005];
int getf(int v)
{
if(fa[v]==v)
return v;
else
{
fa[v]=getf(fa[v]);
return fa[v];
}
}
void merge1(int u,int v)
{
if(getf(u)!=getf(v))
{
fa[getf(v)]=getf(u);
}
}
typedef struct
{
int aa,bb,cc;
}STU1;
STU1 stu[100005];
bool cmp(STU1 x,STU1 y)
{
return x.cc<y.cc;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;
int nm=0;
rep(i,1,m)
{
int a,b,c;
cin>>a>>b>>c;
nm++;
stu[nm].aa=a+1;
stu[nm].bb=b+1;
stu[nm].cc=c;
}
rep(i,1,n)
{
fa[i]=i;
}
sort(stu+1,stu+1+nm,cmp);
ll ans=0;
rep(i,1,m)
{
int u=stu[i].aa;
int v=stu[i].bb;
fa[u]=getf(u);
fa[v]=getf(v);
if(fa[u]==fa[v])
continue;
else
{
ans+=stu[i].cc;
merge1(u,v);
}
}
cout<<ans;
return 0;
}