无人车系统(一):运动学模型及其线性化
相对无人机与机械臂来说,无人车系统的运动学模型非常简洁。尽管简洁,无人车的运动学模型也是非线性的。应用于具体控制算法时,有必要对原始运动学模型进行变形或线性化。本篇主要介绍无人车的运动学模型,并对原始非线性模型进行线性化。
1.从阿克曼转向几何模型到自行车模型
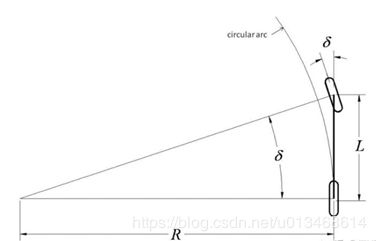
汽车采用阿克曼转向轮,因此模型为如下图所示的阿克曼转向几何模型。
由以上阿克曼转向模型可得进一步简化为车辆单轨模型——自行车模型。
采用自行车模型的好处是它简化了无人车前轮转向角与曲率之间的几何关系,其关系如下式:
t a n ( δ ) = L R tan(\delta)=\frac{L}{R} tan(δ)=RL
其中, δ \delta δ为前轮的转向角, L L L为轴距, R R R则为无人车在该转向角下的运动形成圆的半径(曲率的倒数)。
注意:以上公式可以准确估计低速场景下的车辆运动。 但是,对于高速情况,该公式估计的运动与实际无人车运行的情况有一定的差异,这与路面、轮胎材料都有关系。
2. 无人车运动学模型
曲率半径 R R R与角速度 ω \omega ω、速度 v v v有等式: v = ω R v=\omega R v=ωR,可得无人车的运动学模型如下所示:
{ x ˙ = v c o s ( θ ) y ˙ = v s i n ( θ ) θ ˙ = v t a n ( δ ) L } \left\{\begin{matrix} \dot{x}=vcos(\theta) \\ \dot{y}=vsin(\theta) \\ \dot{\theta}=v\frac{tan(\delta)}{L} \end{matrix}\right\} ⎩⎨⎧x˙=vcos(θ)y˙=vsin(θ)θ˙=vLtan(δ)⎭⎬⎫
其中:
v v v为无人车的速度;
x ˙ \dot{x} x˙为无人车在世界坐标系中X轴方向上的分速度,记为 v x v_{x} vx;
y ˙ \dot{y} y˙为无人车在世界坐标系中Y轴方向上的分速度,记为 v y v_{y} vy;
θ \theta θ为无人车在世界坐标中的航向角;
θ ˙ \dot{\theta} θ˙则为无人车的角速度,可记为 ω \omega ω。
为了突显两个主要控制对象[速度 v v v与角速度 ω \omega ω],对以上无人车运动学模型进行变形,得以下形式:
[ x ˙ y ˙ θ ˙ ] = [ cos θ sin θ 0 ] v + [ 0 0 1 ] w \left[\begin{array}{c}{\dot{x}} \\ {\dot{y}} \\ {\dot{\theta}}\end{array}\right]=\left[\begin{array}{c}{\cos \theta} \\ {\sin \theta} \\ {0}\end{array}\right] v+\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right] w ⎣⎡x˙y˙θ˙⎦⎤=⎣⎡cosθsinθ0⎦⎤v+⎣⎡001⎦⎤w
无人车的速度主要由油门、刹车、以及档位控制;角速度中包含方向盘转向与速度,其中方向盘转向主要由转向系统控制。
3. 运动学模型线性化
参照汽车运动学模型的线性化推导过程,可得到线性化后的无人车运动学模型。
下面给出简略推导过程:
X ˙ = [ x ˙ y ˙ θ ˙ ] = [ v cos θ v sin θ v tan δ L ] = [ f 1 f 2 f 3 ] = f ( X , u ) \dot{X}=\left[\begin{array}{c}{\dot{x}} \\ {\dot{y}} \\ {\dot{\theta}}\end{array}\right]=\left[\begin{array}{c}{v\cos \theta} \\ {v\sin \theta} \\ {\frac{v\tan \delta}{L}}\end{array}\right] =\left[\begin{array}{l}{f_{1}} \\ {f_{2}} \\ {f_{3}}\end{array}\right]=f(X, u) X˙=⎣⎡x˙y˙θ˙⎦⎤=⎣⎡vcosθvsinθLvtanδ⎦⎤=⎣⎡f1f2f3⎦⎤=f(X,u)
其中, X = [ x , y , θ ] T , u = [ v , δ ] T X=\left[x, y, \theta \right]^{T},u=\left[v, \delta \right]^{T} X=[x,y,θ]T,u=[v,δ]T。
我们将上式在点 X r = [ x r , y r , θ r ] T , u r = [ v r , δ r ] T X_{r}=\left[x_{r}, y_{r}, \theta_{r}\right]^{T}, u_{r}=\left[v_{r}, \delta_{r}\right]^{T} Xr=[xr,yr,θr]T,ur=[vr,δr]T处进行泰勒展开(忽略二阶及以上高阶项),可得:
X ˙ = X ˙ − X ˙ r = [ x ˙ − x ˙ r y ˙ − y ˙ r θ ˙ − θ ˙ r ] ≈ ( ∂ f 1 ∂ x ∂ f 1 ∂ v ∂ f 1 ∂ θ ∂ f 2 ∂ x ∂ f 2 ∂ y ∂ f 2 ∂ θ ∂ f 3 ∂ x ∂ f 3 ∂ y ∂ f 3 ∂ θ ) [ x − x r y − y r θ − θ r ] + ( ∂ f 1 ∂ v ∂ f 1 ∂ δ ∂ f 2 ∂ v ∂ f 2 ∂ δ ∂ f 3 ∂ v ∂ f 3 ∂ δ ) [ v − v r δ − δ r ] \dot{X}=\dot{X}-\dot{X}_{r}=\left[\begin{array}{c}{\dot{x}-\dot{x}_{r}} \\ {\dot{y}-\dot{y}_{r}} \\ {\dot{\theta}-\dot{\theta}_{r}}\end{array}\right] \approx \left(\begin{array}{ccc}{\frac{\partial f_{1}}{\partial x}} & {\frac{\partial f_{1}}{\partial v}} & {\frac{\partial f_{1}}{\partial \theta}} \\ {\frac{\partial f_{2}}{\partial x}} & {\frac{\partial f_{2}}{\partial y}} & {\frac{\partial f_2}{\partial \theta}} \\ {\frac{\partial f_{3}}{\partial x}} & {\frac{\partial f_3}{\partial y}} & {\frac{\partial f_3}{\partial \theta}}\end{array}\right)\left[\begin{array}{c}{x-x_{r}} \\ {y-y_{r}} \\ {\theta-\theta_{r}}\end{array}\right]+\left(\begin{array}{cc}{\frac{\partial f_{1}}{\partial v}} & {\frac{\partial f_{1}}{\partial \delta}} \\ {\frac{\partial f_2}{\partial v}} & {\frac{\partial f_2}{\partial \delta}} \\ {\frac{\partial f_3}{\partial v}} & {\frac{\partial f_3}{\partial \delta}}\end{array}\right)\left[\begin{array}{c}{v-v_{r}} \\ {\delta-\delta_{r}}\end{array}\right] X˙=X˙−X˙r=⎣⎡x˙−x˙ry˙−y˙rθ˙−θ˙r⎦⎤≈⎝⎜⎛∂x∂f1∂x∂f2∂x∂f3∂v∂f1∂y∂f2∂y∂f3∂θ∂f1∂θ∂f2∂θ∂f3⎠⎟⎞⎣⎡x−xry−yrθ−θr⎦⎤+⎝⎛∂v∂f1∂v∂f2∂v∂f3∂δ∂f1∂δ∂f2∂δ∂f3⎠⎞[v−vrδ−δr]
由些可得:
Δ X ˙ = A m Δ X + B m Δ u \Delta \dot{X}=A_{m} \Delta X+B_{m} \Delta u ΔX˙=AmΔX+BmΔu
其中: A m = [ 0 0 − v sin θ 0 0 v cos θ 0 0 0 ] A_{m}=\left[\begin{array}{ccc}{0} & {0} & {-v\sin \theta } \\ {0} & {0} & {v\cos \theta} \\ {0} & {0} & {0}\end{array}\right] Am=⎣⎡000000−vsinθvcosθ0⎦⎤, B m = [ cos θ 0 sin θ 0 tan δ L v L cos 2 δ ] B_{m}=\left[\begin{array}{cc}{\cos \theta} & {0} \\ {\sin \theta} & {0} \\ {\frac{\tan \delta}{L}} & {\frac{v}{L\cos ^{2} \delta}}\end{array}\right] Bm=⎣⎡cosθsinθLtanδ00Lcos2δv⎦⎤.
注意:非线性模型经过线性化后,得到的都是增量模型(在当前状态的基础上的增大或减小量),或者说成是局部模型。线性化后的模型只有在线性化点 X r X_r Xr附近才有意义,离线性化点越远,线性化的模型的预测误差越大。
4. 线性模型离散化
由于测量具有离散的本质,现有的物理系统只能被离散的观测与控制。时间维度上的状态都被离散化为一个个状态序列 x 0 , x 1 , . . . , x t , . . . x_0, x_1, ...,x_t,... x0,x1,...,xt,...。但是这些物理系统本质上是连续的,那些状态更新间隔,只是因为我们仅仅能够离散的控制、影响这些系统罢了。
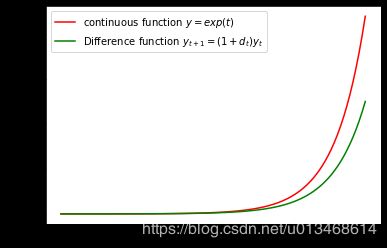
模型的离散化是对物理系统在时间维度的近似。离散化后的差分模型与系统真实的连续模型是有误差的。下图显示了简单一阶常微分方程 y ˙ = y , y 0 = 1.0 \dot{y}=y, y_0=1.0 y˙=y,y0=1.0时的连续状态函数(红色)与差分函数(绿色)(其中, d t = 0.1 s d_t=0.1s dt=0.1s)。表明两者之间是有误差的,并且随着时间增长,误差越大。
为什么有误差,还要将就采用离散的差分形式呢?
一切只因不能立马与差不多就可以十个大字。
不能立马是指控制指令并不能立马从当前值变成期望的控制输入值,因此,就算用连续模型加上阶梯形式控制输入函数计算状态的响应输出也是不准确的。于其不准,倒不如用形式相对简洁易懂的差分模型。另外,并不是所有的系统模型都是可导的,这使得绝大多数情况是被迫采用差分模型。
差不多就可以 由于控制是按一定的周期观测系统内部真实的状态,也即系统的状态初值是不断更新。如果我们的更新周期不是太长,在短时间内,差分函数的状态预测误差是在可接受的范围。
不啰嗦太多!
下面简单推导无人车运动学线性化后连续模型的离散形式:
A m Δ X ( k ) + B m Δ u ( k ) = Δ ˙ ≈ Δ X ( k + 1 ) − Δ X ( k ) T A_m \Delta X(k) + B_m \Delta u(k) =\dot{\Delta}\approx \frac{\Delta X(k+1)-\Delta X(k)}{T} AmΔX(k)+BmΔu(k)=Δ˙≈TΔX(k+1)−ΔX(k)
变形可得:
Δ X ( k + 1 ) = ( 1 + T A m ) Δ X ( k ) + T B m Δ u ( k ) \Delta X(k+1)=(1+TA_m) \Delta X(k) + TB_m \Delta u(k) ΔX(k+1)=(1+TAm)ΔX(k)+TBmΔu(k)
令: A = ( 1 + T A m ) A=(1+TA_m) A=(1+TAm), B = T B m B=TB_m B=TBm,有:
Δ X ( k + 1 ) = A Δ X ( k ) + B Δ u ( k ) \Delta X(k+1)=A \Delta X(k) + B \Delta u(k) ΔX(k+1)=AΔX(k)+BΔu(k)
其中: A = [ 1 0 − v T sin θ 0 1 v T cos θ 0 0 1 ] , B = [ T cos φ 0 T sin φ 0 T tan δ L v T L cos 2 δ ] A=\left[\begin{array}{ccc}{1} & {0} & {-vT\sin \theta } \\ {0} & {1} & {vT\cos \theta} \\ {0} & {0} & {1}\end{array}\right], B=\left[\begin{array}{cc}{T \cos \varphi } & {0} \\ {T \sin \varphi } & {0} \\ {\frac{T\tan \delta }{L}} & {\frac{v T}{L \cos ^{2} \delta}}\end{array}\right] A=⎣⎡100010−vTsinθvTcosθ1⎦⎤,B=⎣⎡TcosφTsinφLTtanδ00Lcos2δvT⎦⎤
总结
本篇介绍无人车运动学模型,之后还介绍了其线性化形式与差分形式。无人车运动学模型在低速时可以较好的预测(估计)系统未来的状态,但是随着车速的提高,汽车侧向动力学特性的影响越来越明显。因此,在高速运行时,一个更加准确的无人车模型必须加入汽车的动力学特性。
模型的用处就是在当前状态给定某控制输入时,预测(估计) 系统未来的状态。控制领域利用模型设计合适的输入,以期控制系统到达目标状态。