深度优先搜索算法与广度优先搜索算法的简单运用:迷宫问题
迷宫问题
迷宫是许多小方格构成的矩形,每个小方格中有的是墙(1),有的是路(0),走迷宫就是从一个小方格沿上下左右四个方向到邻近的方格,当然不能穿墙。设迷宫的入口是左上角1,1,出口是8,8,根据给定的迷宫
a.使用广度优先算法找到迷宫问题的从入口到出口的一条路径
b.使用深度优先算法找到迷宫问题的从入口到出口的一条路径
c.使用回溯法找到迷宫问题的从入口到出口的所有简单路径
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
| 2 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
| 3 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
| 4 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
| 5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
| 6 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
| 7 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
| 8 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
8,8 |
ps:重新认识了 return; 这个语句,该语句表示直接结束当前函数体。如果放到递归里面,也只是结束当前函数体,然后回到递归的上层,只是没有返回值,继续该干嘛干嘛。。。结尾有小测试。
a.广度优先遍历算法
算法思路:
顾名思义,从迷宫的起点开始(起点入队),起点作为当前点,遍历当前点周围的点,如果周围的点符合条件,入队,当前点遍历完成后,出队,在队列中取出队头作为当前点,继续遍历,如果遍历到终点,直接结束遍历。
每次入队的点,记录其前驱,即令这个点入队的当前点。。。
最后按照前驱关系输出路径即可
细节问题代码中解释;
#include
using namespace std;
const int num = 100;
int map[8][8]={{0,0,0,0,0,0,0,0},
{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}}; //存储迷宫
int x[4] = {-1,0,1,0}; //向当前地点相邻的四个点遍历(坐标顺序分别为:上,右,下,左)
int y[4] = {0,1,0,-1};
int x_queue[num]; //存储队列中的点的坐标
int y_queue[num];
int route[num]; //存储每个点的前驱点
int front, end; //队头,队尾
void out(int n) { //输出函数
if (n == 0) {
cout << '(' << x_queue[0] << ',' << y_queue[0] << ')' << endl;
return ;
}
out(route[n]);
cout << '(' << x_queue[n] << ',' << y_queue[n] << ')' << endl;
}
bool bfs() { //遍历函数
while (front != end) {
for (int i = 0; i < 4; i++) {
int x_now = x_queue[front]+x[i];
int y_now = y_queue[front]+y[i];
if ((x_now >= 0 && x_now < 8) && (y_now >= 0 && y_now < 8) && (map[x_now][y_now] == 0)) { //当周围的点符合条件,入队,条件为点在矩阵内,点不是墙,点没有走过
map[x_now][y_now] = 2; //走过的点赋值为2,不重复走
x_queue[end] = x_now;
y_queue[end] = y_now;
route[end] = front; //记录该入队的点的前驱,即当前正在遍历的点
if (x_now == 7 && y_now == 7)
return true;
end++;
}
}
front++;
}
return true;
}
int main() {
front = 0;
end = 1;
x_queue[0] = 0;
y_queue[0] = 0;
route[0] = 0;
map[0][0] = 2;
if (bfs() == true) {
cout << "存在破解路径" << endl;
out(end);
}
else {
cout << "不存在破解路径" << endl;
}
return 0;
}
b.深度优先遍历算法
算法分析:
属于广度遍历的兄弟算法,从起点的某个方向一直走,走到尽头,存在路径返回true,否则退回到上一个"分叉口",选择另一个方向走到尽头。
一开始做法是方法1,后来做到第三题,发现这个做法更倾向第三题的回溯法解答,于是产生了第二种做法,当然,思路是一样的。
方法1:
#include
using namespace std;
const int num = 100;
int map[8][8]={{0,0,0,0,0,0,0,0},
{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}}; //存储迷宫
int x_coord[4] = {-1,0,1,0}; //向当前地点相邻的四个点遍历(坐标顺序分别为:上,右,下,左)
int y_coord[4] = {0,1,0,-1};
int x_queue[num]; //存储路径中的点的坐标
int y_queue[num];
int n;
void out() { //输出函数
for (int i = 0; i <= n; i++) {
cout << '(' << x_queue[i] << ',' << y_queue[i] << ')' << endl;
}
}
bool dfs(int x, int y) { //遍历函数
x_queue[n] = x;
y_queue[n] = y;
if (x == 7 && y == 7) return true;
else {
bool flag = false;
for (int i = 0; i < 4; i++) {
int x_now = x+x_coord[i];
int y_now = y+y_coord[i];
if ((x_now >= 0 && x_now < 8) && (y_now >= 0 && y_now < 8) && (map[x_now][y_now] == 0)) {
flag = true;
map[x_now][y_now] = 2;
n++;
if (dfs(x_now,y_now)) //如果此路能走,返回ture,否则,返回false
break;
else
flag = false;
map[x_now][y_now] = 0;
n--;
}
}
return flag;
}
}
int main() {
n = 0;
if (dfs(0,0) == true) {
cout << "存在破解路径" << endl;
out();
}
else {
cout << "不存在破解路径" << endl;
cout << n << endl;
}
return 0;
} 方法2:
#include
using namespace std;
const int num = 100;
int map[8][8]={{0,0,0,0,0,0,0,0},
{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}}; //存储迷宫
int x_coord[4] = {-1,0,1,0}; //向当前地点相邻的四个点遍历(坐标顺序分别为:上,右,下,左)
int y_coord[4] = {0,1,0,-1};
int n;
bool flag;
void out() { //输出函数
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 8; j++) {
cout << map[i][j] << ' ';
}
cout << endl;
}
}
void dfs(int x, int y) { //遍历函数
map[x][y] = 2;
for (int i = 0; i < 4; i++) {
int x_now = x+x_coord[i];
int y_now = y+y_coord[i];
if ((x_now >= 0 && x_now < 8) && (y_now >= 0 && y_now < 8) && (map[x_now][y_now] == 0)) {
map[x_now][y_now] = 2;
if (x_now == 7 && y_now == 7) {
flag = true;
out();
}
else
dfs(x_now,y_now);
}
}
}
int main() {
n = 0;
flag = false;
dfs(0,0);
if (flag == false) {
cout << "不存在破解路径!" << endl;
}
return 0;
}
c.回溯法
回溯法既是通过深度优先遍历算法的思想,把任何能够走出的迷宫的路径的输出来。
#include
using namespace std;
const int num = 100;
int map[8][8]={{0,0,0,0,0,0,0,0},
{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}}; //存储迷宫
int x_coord[4] = {-1,0,1,0}; //向当前地点相邻的四个点遍历(坐标顺序分别为:上,右,下,左)
int y_coord[4] = {0,1,0,-1};
int x_queue[num]; //存储路径中的点的坐标
int y_queue[num];
int n;
int routes;
void out() { //输出函数
routes++;
cout << "总步数:" << n+1 << endl;
for (int i = 0; i < n; i++) {
cout << '(' << x_queue[i] << ',' << y_queue[i] << ") ";
}
cout << '(' << x_queue[n] << ',' << y_queue[n] << ")\n" << endl;
}
void dfs(int x, int y) { //遍历函数
x_queue[n] = x;
y_queue[n] = y;
map[x][y] = 2;
if (x == 7 && y == 7) {
out();
return ;
}
else {
for (int i = 0; i < 4; i++) {
int x_now = x+x_coord[i];
int y_now = y+y_coord[i];
if ((x_now >= 0 && x_now < 8) && (y_now >= 0 && y_now < 8) && (map[x_now][y_now] == 0)) {
map[x_now][y_now] = 2;
n++;
dfs(x_now, y_now);
map[x_now][y_now] = 0;
n--;
}
}
}
}
int main() {
n = 0;
routes = 0;
dfs(0, 0);
if (routes == 0) {
cout << "不存在破解路径 "<< endl;
}
else {
cout << "破解路径:" << routes << "条" << endl;
}
return 0;
}
很明显以上的深度优先遍历算法输出的路径不一定是最短路径,因为设置为只要找到路径立即输出,如果想要找到最小路径,那么把所有可能存在的路径找出来是必不可少的,利用c的回溯法思想就能达到目的
补充一个利用深度遍历算法找最短路径的算法:
#include
using namespace std;
const int num = 100;
int map[8][8]={{0,0,0,0,0,0,0,0},
{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}}; //存储迷宫
int x_coord[4] = {-1,0,1,0}; //向当前地点相邻的四个点遍历(坐标顺序分别为:上,右,下,左)
int y_coord[4] = {0,1,0,-1};
int x_queue[num]; //存储路径中的点的坐标
int y_queue[num];
int x_min[num]; //存储最佳路径
int y_min[num];
int n;
int Min;
void out() { //输出函数
cout << "最少步数:" << Min+1 << endl;
for (int i = 0; i < Min; i++) {
cout << '(' << x_min[i] << ',' << y_min[i] << ") ";
}
cout << '(' << x_min[Min] << ',' << y_min[Min] << ")\n" << endl;
}
void dfs(int x, int y) { //遍历函数
x_queue[n] = x;
y_queue[n] = y;
map[x][y] = 2;
if (x == 7 && y == 7) {
if (Min > n) {
Min = n;
for (int i = 0; i <= n; i++) {
x_min[i] = x_queue[i];
y_min[i] = y_queue[i];
}
}
return ;
}
else {
for (int i = 0; i < 4; i++) {
int x_now = x+x_coord[i];
int y_now = y+y_coord[i];
if ((x_now >= 0 && x_now < 8) && (y_now >= 0 && y_now < 8) && (map[x_now][y_now] == 0)) {
map[x_now][y_now] = 2;
n++;
dfs(x_now, y_now);
map[x_now][y_now] = 0;
n--;
}
}
}
}
int main() {
n = 0;
Min = num;
dfs(0, 0);
if (Min == num) {
cout << "不存在破解路径 "<< endl;
}
else {
cout << "存在破解路径:" << endl;
out();
}
return 0;
}
PS:
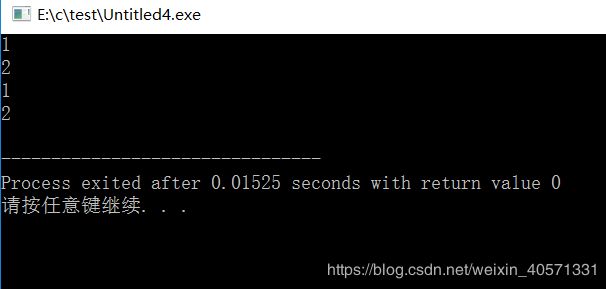
return; 语句 彩蛋。。。
#include
using namespace std;
void fun(int n) {
for (int i = 0; i < 2; i++) {
cout << n << endl;
if (n == 2) return ;
else
fun(n+1);
}
}
int main() {
fun(1);
return 0;
} 嗯。。。输出了两次1,2,很明显,return结束后,返回到上层,继续没有完成的循环。。。
所以,return; 语句的功能是直接结束当前函数体;
有些同学可能会纳闷这不是很显然的事吗?一般我们在利用递归解题时,常常返回之后函数就不做多余的操作了,所以不注意的话,可能会理所当然的认为,这就是结束语句,而且我们常常学习时都会把它(return ;)称为递归出口。