数字信号处理实验(六)—— 心电信号处理 IIR FIR滤波综合题(下篇)
-
2️⃣产生模拟工频信号,与干净心电混合,设计一个带阻滤波器(50Hz陷波器)滤除心电信号中的电源线干扰,调整工频幅度大小,对滤波前后的心电信号的频谱进行分析比较。
-
其中带阻滤波器指标要求:
- 通带下限频率Wp1=0.18 π \pi π
- 阻带下截止频率Ws1=0.192 π \pi π
- 阻带上截止频率Ws2=0.208 π \pi π
- 通带上限频率Wp2=0.22 π \pi π
- 阻带衰减不小于15dB,
- 通带衰减不大于1dB。
-
总要求:
- 编写IIR带阻滤波器仿真程序,在屏幕上打印出数字滤波器的频率区间[0, π \pi π]上的幅频响应特性由线( ∣ H ( e j ω ) ∣ |H(e^{j\omega})| ∣H(ejω)∣)
- 计算其对含工频干扰的心电信号的带阻滤波响应序列, 并在屏幕上打印出干净心电信号波形,含工频干扰的心电信号波形以及滤波后的信号波形,并进行比较
- 同时对滤波前后的心电信号的频谱进行分析比较,并在屏幕上打印出滤波前后的心电信号的频谱,观察其变化。
-
% IIR 带阻滤波 工频信号
clear all;
clc;
val=importdata('Ecg.txt');
%导入心电信号Ecg.txt,其中fs=500Hz。
signal=val(1,1:1800);
fs=500;
subplot(3,2,2);
plot(signal);
title('原始ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
grid on ;
subplot(3,2,4);
av = 100;
f0=50;
t=[1:length(signal)];
noise=av*cos(2*pi*f0*t/fs);
sig_with_noise = noise+signal;
plot(sig_with_noise);
title('添加工频噪声的ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
grid on;
% 通带截止频率 0.1 pi 阻带截止频率 0.16 pi
% 阻带衰减15db 通带衰减1db
Fs=1;
wp=[0.18, 0.22];
ws=[0.192, 0.208];
Rp=1;
Rs=19;
[N, wn]=buttord(wp, ws, Rp, Rs);
[b,a]=butter(N,wn,'stop');
[H,w]=freqz(b, a);
grid on;
x=linspace(0,1800,1800);
subplot(3,2,6);
m=filter(b,a,sig_with_noise);
plot(x,m);
title('带阻滤波后 ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
N=2048;
subplot(3,2,1);
mf=fft(signal,N); %进行频谱变换(傅里叶变换)
mag=abs(mf);
f=(0:length(mf)-1)*Fs/length(mf); %进行频率变换
plot(f,mag);
%axis([0,1500,1,50]);
title('原始ECG信号 FFT分析');
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');
subplot(3,2,3);
mfa=fft(sig_with_noise,N); %进行频谱变换(傅里叶变换)
maga=abs(mfa);
fa=(0:length(mfa)-1)*Fs/length(mfa); %进行频率变换
plot(fa,maga);
title('添加工频噪声的ECG信号 FFT分析');
%axis([0,1500,1,50]);grid; %画出频谱图
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');
subplot(3,2,5);
mfa=fft(m,N); %进行频谱变换(傅里叶变换)
maga=abs(mfa);
plot(fa,maga);
title('带阻滤波后 ECG信号 FFT分析');
%axis([0,1500,1,50]);grid; %画出频谱图
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');
IIR带阻滤波器的幅频响应图如下:
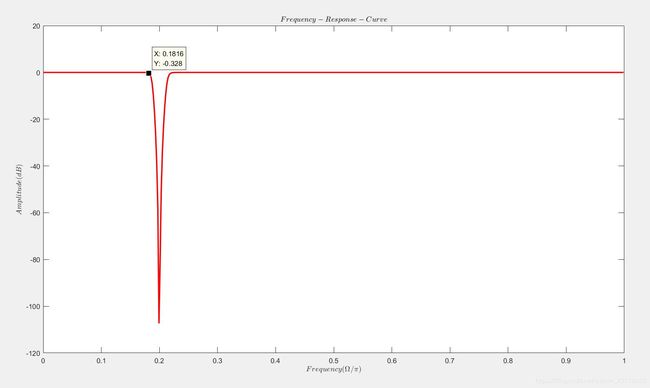
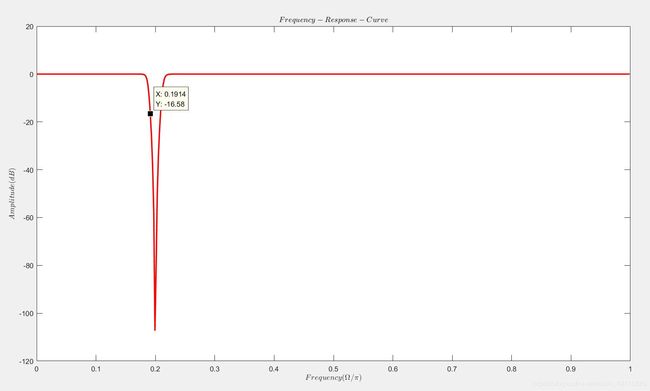
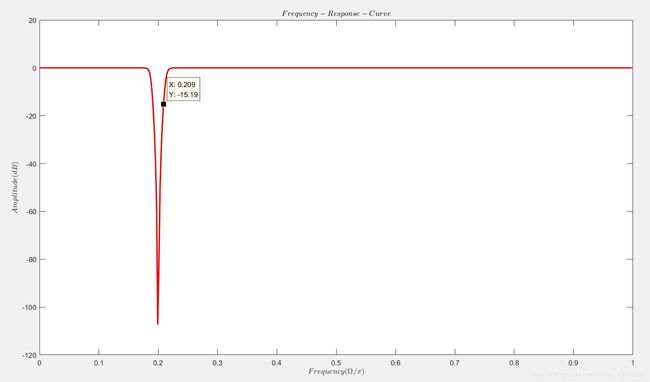
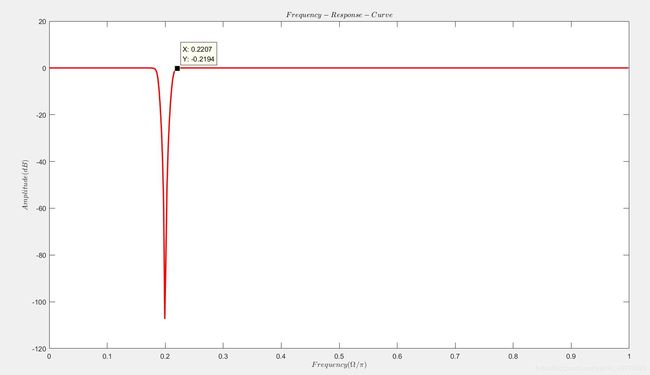
最终信号滤波前后的对比图:
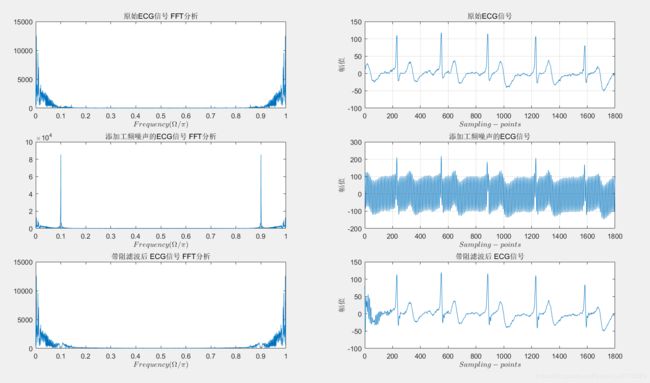
-
3️⃣产生模拟基线漂移信号,与干净心电信号混合,设计一个高通滤波器滤除心电信
号中的基线低频干扰,调整基线的幅度大小,对滤波前后的心电信号的频谱进行分析比较。-
高通滤波器指标要求:
- 通带截止频率Wp=0.0028 π \pi π
- 阻带截止频率Ws=0.0012 π \pi π
- 阻带衰减不小于15dB
- 通带衰减不大于1dB
-
要求:
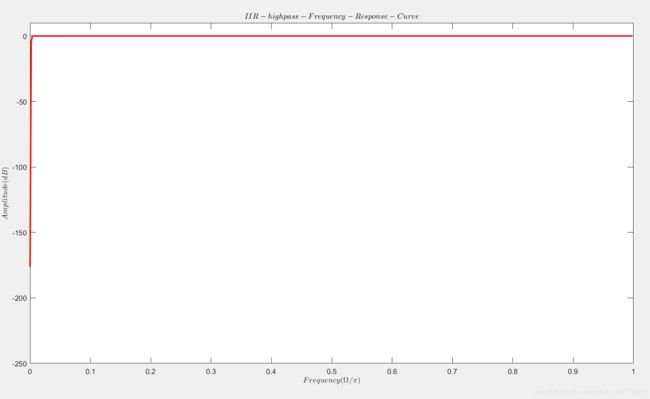
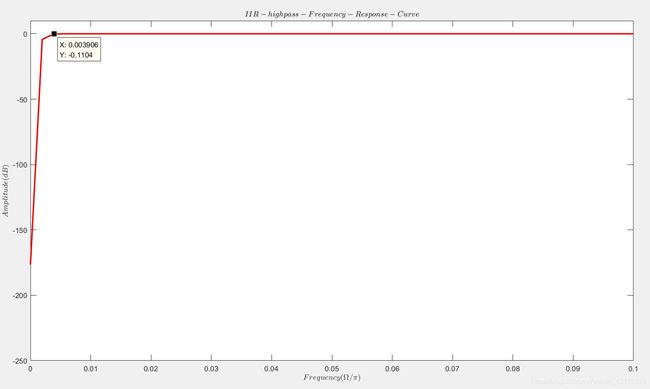
- 编写IIR高通滤波器(或FIR高通滤波器)仿真程序,在屏幕上打印出数字滤波器的频率区间 [0, π \pi π]上的幅频响应特性曲线
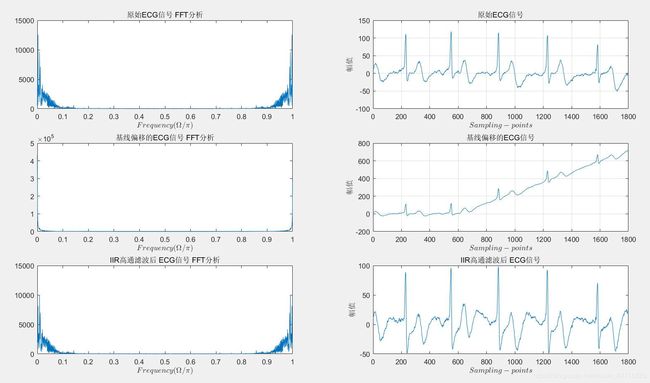
- 计算其对含基线低频干扰的心电信号的高通滤波响应序列,并在屏幕上打印出干净心电信号波形,含基线低频干扰的心电信号波形以及滤波后的信号波形,并进行比较
- 同时对滤波前后的心电信号的频谱进行分析比较,并在屏幕上打印出滤波前后的心电信号的频谱,观察其变化。
-
% IIR 高通滤波 基线偏移的心电信号
clear,clc;
val=importdata('Ecg.txt');
%导入心电信号Ecg.txt,其中fs=500Hz。
signal=val(1,1:1800);
fs=500;
subplot(3,2,2);
plot(signal);
title('原始ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
grid on ;
subplot(3,2,4);
n1=length(signal)/3;
x1=zeros(1,n1);
t=1:length(signal)-n1;
x2=(length(signal)-n1)/2000*(t-1)+1;
noise=[x1,x2];
sig_with_noise = noise+signal;
plot(sig_with_noise);
title('基线偏移的ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
grid on;
% 通带截止频率 0.1 pi 阻带截止频率 0.16 pi
% 阻带衰减15db 通带衰减1db
Rp=1;
Rs=15;
Fs=1;
Ts=1/Fs;
wpz=0.0028/Fs;
wsz=0.012/Fs;
wp=2*Fs*tan(wpz*pi/2);
ws=2*Fs*tan(wsz*pi/2);
[N,Wn]=buttord(wp,ws,Rp,Rs,'s');
[Z,P,K]=buttap(N);
[Bap,Aap]=zp2tf(Z,P,K);
[b,a]=lp2hp(Bap,Aap,Wn);
[bz,az]=bilinear(b,a,Fs);
grid on;
x=linspace(0,1800,1800);
subplot(3,2,6);
m=filter(bz,az,sig_with_noise);
plot(x,m);
title('IIR高通滤波后 ECG信号');
ylabel('幅值');
xlabel({ '$$ Sampling-points $$' },'Interpreter','latex');
N=2048;
subplot(3,2,1);
mf=fft(signal,N); %进行频谱变换(傅里叶变换)
mag=abs(mf);
f=(0:length(mf)-1)*Fs/length(mf); %进行频率变换
plot(f,mag);
%axis([0,1500,1,50]);
title('原始ECG信号 FFT分析');
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');
subplot(3,2,3);
mfa=fft(sig_with_noise,N); %进行频谱变换(傅里叶变换)
maga=abs(mfa);
fa=(0:length(mfa)-1)*Fs/length(mfa); %进行频率变换
plot(fa,maga);
title('基线偏移的ECG信号 FFT分析');
%axis([0,1500,1,50]);grid; %画出频谱图
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');
subplot(3,2,5);
mfa=fft(m,N); %进行频谱变换(傅里叶变换)
maga=abs(mfa);
plot(fa,maga);
title('IIR高通滤波后 ECG信号 FFT分析');
%axis([0,1500,1,50]);grid; %画出频谱图
xlabel({ '$$ Frequency(\Omega/\pi) $$' },'Interpreter','latex');