DoubleArrayTrie : DAT双数组Trie树
本文参考: http://www.cnblogs.com/ooon/p/4883159.html
推荐:
码农场的《双数组Trie树(DoubleArrayTrie)Java实现》
外文《An Implementation of Double-Array Trie》
DoubleArrayTrie
双数组Tire树是Tire树的升级版,Tire取自英文Retrieval中的一部分,即检索树,又称作字典树或者键树。
双数组Tire树,其基本观念是压缩trie树,使用两个一维数组BASE和CHECK来表示整个树。它是由三个日本人提出的一种Trie树的高效实现 ,兼顾了查询效率与空间存储。
双数组缺点在于:构造调整过程中,每个状态都依赖于其他状态,所以当在词典中插入或删除词语的时候,往往需要对双数组结构进行全局调整,灵活性能较差。 如果核心词典已经预先建立好并且有序的,并且不会添加或删除新词,那么这个缺点是可以忽略的。所以常用双数组Tire树都是载入整个预先建立好的核心分词词典。
双数组Tire树拥有Tire树的所有优点,而且刻服了Tire树浪费空间的不足,使其应用范围更加广泛,例如词法分析器,图书搜索,拼写检查,常用单词过滤器,自然语言处理 中的字典构建等等。
在基于字典的分词方法中,许多开源的实现都采用了双数组Tire树。Ansj便是用DAT构造词典用作初次分词,极大地节省了内存占用。
DoubleArrayTrie实现
Tire树终究是一颗树形结构,树形结构的两个重要要素便是前驱和后继,把Tire树压缩到双数组中,只需要保持能查询到每个节点的前驱和后继即可。Tire树中几个重要的概念。
- STATE:状态,实际为在数组中的下标
- CODE : 状态转移值,实际为转移字符的 ASCII码, java中使用(int)(char c)和(char)(int i)互相转
- BASE :表示后继节点的基地址的数组,叶子节点没有后继,标识为字符序列的结尾标志
- STATE:状态,实际为在数组中的下标
在DAT的构造过程中,一般有两种构造方法,动态构造双数组和静态构造。
1、动态输入词语,动态构造双数组 :
对于一个接收字符c从状态s移动到t的转移,在双数组中保存的条件是
base[0] = 1
base[s] + c =t
check[t] = s, 即 check[ base[s] + c ] = s
2 已知所有词语,静态构造双数组:
开源项目:darts-java
darts-java的第一个改进就是另字符的code = ASCII+1
darts-java对双数组算法做的第二个改进就是:
base[0] = 1
base[s] +c = t
check[t] = base[s]
这两个改进的匹配演算可以参考码农场的《双数组Trie树(DoubleArrayTrie)Java实现》
以下所有解析都是基于darts-java的两个改进
base和check数据的构造过程
1 建立根节点root,令base[root] =1
2 找出root的子节点 集{root.childreni }(i = 1…n) , 使得 check[root.childreni ] = base[root] = 1
3 对 each element in root.children :
1)找到{elemenet.childreni }(i = 1…n) ,注意若一个字符位于字符序列的结尾,则其孩子节点包括一个空节点,其code值设置为0找到一个值begin使得每一个check[ begini + element.childreni .code] = 0,即都不存在
2)设置base[element.childreni] = begini
3)对element.childreni 递归执行步骤3,若遍历到某个element,其没有children,即叶节点,则设置base[element]为负值(一般为在字典中的index取负)
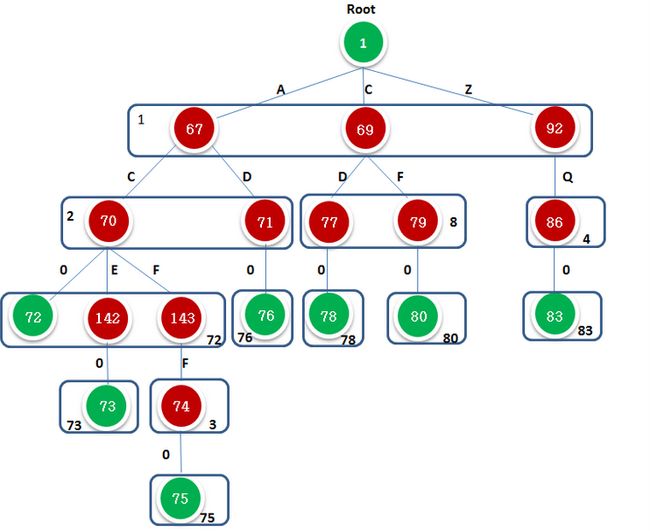
例子:
模式为: { AC,ACE,ACFF,AD,CD,CF,ZQ }
1、由code= ASCII+1, 以及i = base[0] + code可以得到下面每个字符的状态:
root A C D E F Q Z
i 0 67 69 92
code 0 66 68 69 70 71 82 912、 由定义可知以及构造过程的第2点,距离root节点深度为1的所有children其check[root.childreni ] = base[root] = 1,在模式串中root的三个子节点’A’, ‘C’, ‘E’的check值=1, 假设root经过A C Z 的作用分别到达三个状态 t1 t2 t3得到下面矩阵:
root A C Z
i 0 67 69 92
base 1
check 0 1 1 1
state t0 t1 t2 t3 3、由上面步骤,我们知道:状态t1是由条件 ‘A’ 触发的,那么‘A’的base值是多少呢?由定义和构造过程步骤3知道:‘A’的子节点值{C D}, 找一个begin值,使得check[begin + ‘C’.code] = check[begin +’D’,code] = 0, 即check[begin + 68] = check[begin + 69] = 0,
假设begin = 0. 那么check[0+ 69] 存在字符‘C’, check[begin + 68] = check[begin + 69] = 0不成立。直到begin = 2,使得check[begin + 68] = check[begin + 69] = 0成立。
此时,base[t1] = begin = 2, 状态t1 =67。
t4 = base[t1]+ ‘C’.code = 70 = 2 + 68 ,
t5 = base[t1] +’D’.code = = 2 + 69 = 71, check[t5] = check[t4] = base[t1] = 2, 得到如下矩阵:
root A C Z C D
i 0 67 69 92 70 71
base 1 2
check 0 1 1 1 2 2
state t0 t1 t2 t3 t4 t5 4、按照步骤3,求得状态t2,字符‘C’的base[t2] = begin = 8, 下一状态,即子节点值{D, F}的t6,t7状态。
t6 = base[t2] + ‘D’.code = 8 + 69 = 77;
t7 = base[t2] + ‘F’.code = 8 + 70 = 79;
check[t6] = check[t7] = base[t2] = begin = 8;矩阵如下:
root A C Z C D D F
i 0 67 69 92 70 71 77 79
base 1 2 8
check 0 1 1 1 2 2 8 8
state t0 t1 t2 t3 t4 t5 t6 t75、通过一系列计算之后,最终矩阵如下:
root A C Z C D D F Q E F F
i 0 67 69 92 70 71 77 79 86 142 143 74
base 1 2 8 4 72 76 78 80 83 73 3 75
check 0 1 1 1 2 2 8 8 4 72 72 3
state t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t116、注意没有儿子的叶节点,设置其base值为-index。根据模式串的输出补全后得到矩阵如下:
root A C Z C D D F Q E F F AC AD CD CF ZQ ACE ACFF
i 0 67 69 92 70 71 77 79 86 142 143 74 72 76 78 80 83 73 75
base 1 2 8 4 72 76 78 80 83 73 3 75 -1 -4 -5 -6 -7 -2 -3
check 0 1 1 1 2 2 8 8 4 72 72 3 72 76 78 80 83 73 75
state t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 按照上诉矩阵,使用DFA的形式来描绘,节点表示state,字符作为转移条件,不同字符触发不同的state,可得到到树如下图(图片来源:http://www.cnblogs.com/ooon/p/4883159.html)。其中红色部分正好是第5步骤的矩阵;绿色部分是按照模式集合得到的ouput表。